Hybrid Continuous-Time MILP Model for Crude Oil Scheduling under the Influence of High Tides
Zhou Zhiju; Zhou Xiang; Zhou Han
(SINOPEC Research Institute of Petroleum Processing, Beijing 100083)
Abstract: Vessels, especially very large or ultra large crude carriers (VLCCs or ULCCs), often can only dock and leave the berth during high tide periods to prevent being stranded.Unfortunately, the current crude scheduling models do not take into account tidal conditions, which will seriously affect the feasibility of crude schedule.So we first focus on the docking and leaving operations under the tidal actions, and establish a new hybrid continuous‐time mixed integer linear programming(MILP) model which incorporates global event based formulation and unit‐specific event based formulation.Upon considering that the multiple blending of crude oil can easily cause the production fluctuating, there are some reasonable assumptions that storage tanks can only store pure crude, and charging tanks just can be refilled after being emptied, which helps us obtain a simple MILP model without composition discrepancy caused by crude blending.Two cases are used to demonstrate the efficacy of proposed scheduling model.The results show that the optimization schedule can minimize the demurrage of the vessels and the number of feeding changeovers of crude oil distillation units (CDUs).
Key words: crude scheduling; tide; continuous‐time representation; mixed integer linear programming
1 Introduction
In the past ten years, the consumption of crude oil accounting for the largest share of primary energy has been steadily increasing, and as of 2019, the crude consumption reached 98.27 million barrels per day.Assuming that crude oil price is equal to 60 dollars per barrel, the daily purchase cost will be 5.9 billion dollars.As a consequence, a slight optimization of crude oil utilization is able to bring about considerable economic benefits to enterprises, and optimizing crude oil schedule is a good way to realize this process, because it can give play to the economic value of cheap crude oil and reduce vessels demurrage.
The establishment of mathematical programming models as the mainstream method is used to optimize the crude oil schedule.After more than 20 years of hard work, these models have been greatly improved in terms of industrial applicability, time representation, and nonlinear constraint processing.
Lee, et al.[1]first proposed a complete discrete-time mixed integer linear programming (MILP) model for crude oil scheduling problem, which involved the unloading from vessels to storage tanks, the transfer of oil between storage tanks and charging tanks, the oil blending in charging tanks, and the moving of oil to crude oil distillation units (CDUs) from charging tanks.Their model was the basis for many studies, but linear constraints on the properties of the mixed crude oil would cause the component concentrations of crude oil in the charging tank to be inconsistent with that discharged from the same tank.This phenomenon is known as composition discrepancy[2].
Li, et al.[3]extended the model proposed by Lee, et al.[1]to consider the allocation of multi‐berths to vessels and developed an iterative MILP‐NLP (non‐linear programming) combinational algorithm to address the composition discrepancy.The iterative algorithm is popular[4‐6], and many scholars have worked hard to produce tight MILP relaxation for fast convergence[7‐10].But even if it exists, it may not find any solution[5,11‐12], and the calculation efficiency is low due to the introduction ofa large number of binary variables[12].
Jia, et al.[13]introduced the unit‐specific event‐based continuous time representation for crude oil scheduling,which has computational advantages because of the fewer variables and constraints.Unfortunately, their model also had the phenomenon of composition discrepancy.
Reddy, et al.presented a discrete‐time formulation[14]and a continuous‐time formulation based on global time slot[15]to describe some real‐life operations such as the unloading of VLCCs through a single‐buoy mooring(SBM) pipeline with a non‐negligible holdup, brine settling needed for tanks after receiving crude.However,their model lacked the transportation between tanks.They proposed a rolling‐horizon solution strategy to transform a non-convex mixed integer nonlinear programming(MINLP) model into a series of MILP models.Although the algorithm was effective for certain problems, there was still the risk of not being able to obtain a feasible solution, and it took a long time for solving the industrial problems[16].
Based on Reddy’s discrete time model, Li, et al.[16]developed a partial relaxation strategy and a backtracking strategy to improve the algorithm’s robustness and efficiency, and considered 15 crude oil blending indicators to extend the industrial applicability of the model.Later,they proposed an event‐based continuous time MINLP model[12]for the same problem mentioned above, which was solved by a MILP‐NLP algorithm with piecewise‐linear underestimations of the bilinear terms.
The above models were based on time slots or event points to determine the order of execution of each operation.Mouret, et al.first established the continuous time single‐operation sequencing (SOS)[17]and multi‐operation sequencing (MOS)[18]MINLP formulations based on priority‐slots for the problem described by Lee,et al.[1]In their models, the sequence of priority slots indicated the sequence of non‐overlapping operations.They introduced symmetry‐breaking constraints to narrow the search space of solutions and used a MILP‐NLP procedure to solve the non‐convex MINLP model.
The pipeline between storage tanks and charging tanks may be hundreds of kilometers long.Thus, it takes a long time for the crude oil to move from the inlet to the outlet of the pipeline.To this end, Zhang, et al.[19], Qu, et al.[20]and Cafaro, et al.[4]had proposed a unit‐specific event‐based model and a general precedence based model,respectively, and used the MILP‐NLP iterative algorithm and the MINLP solution algorithm to address the long‐distance pipeline transportations.
After years of research, the crude oil scheduling models have considered increasingly complex refinery structures and operations, but no existing work, to our knowledge,focuses on the impact of tidal action on the berthing and departure of vessels.As we all known, vessels, especially VLCCs and ULCCs, have large carrying capacity and require ports with large water depths to berth and depart safely.However, the water depth of the port usually cannot meet the navigation requirements of large vessels,so crews often berth or depart the port at high tide to prevent the vessels from stranding on the sand and avoid huge economic losses.Therefore, tidal activity needs to be considered to enhance the feasibility of the model solutions.This will also be our research focus.
Time representation and bilinear constraints are the two major factors affecting the calculation efficiency of the crude oil scheduling model.Because the scale of the continuous‐time model is smaller than that of the discrete-time model for the same problem[21], the solution efficiency of the former is often better than that of the latter.According to whether all units or operations share the same set of time variables, the continuous time representations mentioned above are divided into the global time based formulation and the unit‐specific based formulation[22].The unit‐specific based one produces a smaller-scale model for the same problem[23], but causes more big‐M constraints which reduce the computational speed of the model[24].Hence, upon considering comprehensively, we propose a novel continuous time representation, which is a mixture of global time grid and unit‐specific time grid.
How to quickly solve the MINLP model including bilinear constraints is a relatively difficult task.The current mainstream processing method is to decompose the MINLP model into the MILP model and the NLP model[3].The method cannot guarantee the convergence and robustness of the model[12].In fact, for complex enterprise scheduling problems, even the pure MILP model is difficult to obtain a feasible solution in severalhours[23].Therefore, in order to meet the needs of complex industrial problems, we make reasonable assumptions and establish a pure MILP model without composition discrepancy.
2 Problem Statement
At first we consider the scheduling problem described by Lee, et al.[1], which consists of crude oil unloading,storage, transportation, blending, and processing as illustrated in Figure 1.The arriving vessels can dock at any free berth, but if all berths are busy, it must wait until the previous vessel is empty.It is worth mentioning that for safety reasons, VLCCs and ULCCs are proposed to berth at high tide, because they can run aground on the beach at low tide, and they exhibit the same characteristics when leaving the port.Then, unloading operation starts after the vessel docks.Both pure oil and mixed oil are allowable in storage tanks (STs), but in order to determine the accurate unloaded amount and maintain the crude quality, blending operation should be avoided as much as possible at the refinery[23].Next, multiple types of oil from STs are transferred into charging tanks (CTs), and are then mixed in CTs or pipelines between STs and CTs.Here we only consider the pipeline blending process because it can better guarantee the quality of mixed crude oil than tank blending.In addition, the following will prove that this processing can ensure the linearity of the scheduling model.Finally, the mixed oil meeting the quality requirements is fed into the CDUs.

Figure 1 Schematic diagram of crude oil scheduling
The schedule of crude oil is to determine the execution time of above operations and the transfer volume of crude oil to minimize the operational cost or maximize the distillation profits for the refinery.
(1) The detailed docking schedule, including the time and location of each vessel’s docking.
(2) The detailed unloading schedule, including the time,destination and quantity of crude oil to be unloaded.
(3) The detailed transfer schedule, including the time,connection and quantity of transfer operations.
(4) The detailed feeding schedule, including the feeding time, location, and quantity of crude oil transferred.
(5) The inventory level and composition profiles of each tank.
In order to determine these schemes, some basic information should be known in advance as shown below.
(1) The refinery configuration, including the numbers of berths, STs, CTs and CDUs, and their interconnections.
(2) The operational limits, including the flow‐rate limits of each operation, the capacity of tanks, the allowable types of crude in tanks, and the minimum brine settling time.
(3) The initial state of berths and tanks, and the initial inventory of tanks.
(4) The blending proportion for mixed oil.
(5) The start and termination time of the scheduling horizon.
(6) The tidal table during the scheduling horizon.
(7) The vessels arrival information, including the arrival time, the types and quantity of crude oil carried.
(8) The production demand for objective mixed crude.
In addition to the above information, we also extract different constraints for oil unloading, transportation, and processing to formulate the crude schedule.More details will be introduced in Section 3.
3 MILP Formulation
We should establish a MILP model to solve the crude scheduling problem.In order to balance the model’s complexity and computing performance, the following assumptions are specified:
(1) Vessels can only dock and leave at certain specific times when high tide occurs.
(2) All vessels are empty before the end of the scheduling horizon.
(3) Blending operations are not allowed in storage tanks.
(4) The type of crude oil can only be determined by some specific key components.
(5) A charging tank can feed at most one CDU, and a CDU can be fed by one charging tank.
(6) The charging tank can be disconnected from a CDU only after it is empty.
Next, we will describe the comprehensive model expression.
3.1 Time representation constraints
We have established a hybrid continuous time model that integrates global time grid and unit‐specific grid,involving the global time set and the unloading‐time set,respectively.
(1) The global time set
The global time set is to specify the execution time of each feeding operation of charging tanks and CDUs, and to limit the boundary of time variables in the unloading‐time set.

(2) The unloading‐time set
We stipulate that each berth has an independent time grid in the unloading‐time set, which is an unit‐specific representation, and the slotsof berthbmust be included in the slotsof the global time grid.

3.2 Vessel arrival and departure rules
Four binary variablesSDVLBEvbs,EDVLBEvbs,STVLvt, andSTVLvtare set to ensure that vessels can only dock and leave in certain time segments.
(1) Vessels have only one opportunity to dock at one docking station.

(2) The docking initiation time of vesselvis equal to the start time of slotson the berthb,when the variableSDVLBEvbsis activated.

(3) The docking completion time of vesselvis the same as the end time of slotson the berthb,when the variableEDVLBEvbsis activated.

(4) Vessels can berth and depart at any time during a high tide.

(5) The time to start docking should be later than its arrival time, and earlier than the departure time.

(6) The vessel that arrives first docks first.

(7) The vesselvcan only leave the berth after being completely unloaded.

3.3 Vessel unloading operations
(1) Vesselvcan only berth between the beginning and the end of the mooring.
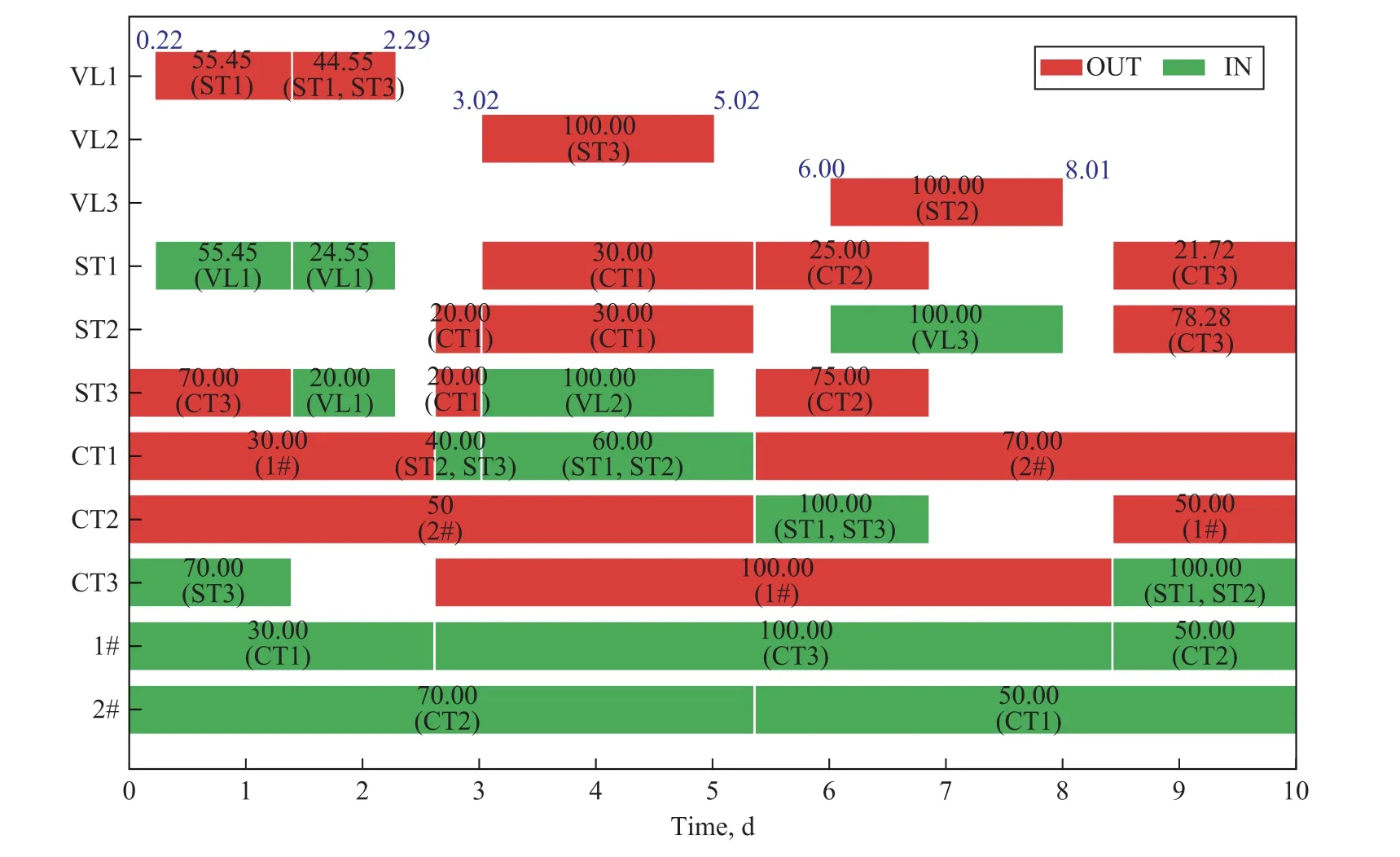
When the vesselvfirst docks at the berthbin the time slotsor the previous time slot (ss (2) The unloading operations can only be performed after vessels have docked. (3) The unloading rate cannot exceed upper limits. (4) Each crude oil operation should comply with the material balance restriction. (1) The input volume of the berthbshould be consistent with its output volume. (2) Only one vessel can be moored in the docking station at the same time. (1) Charging and discharging constraints The storage tankimust be receiving oil when its inventory level increases.Binary variableBISTBEibsexpresses that the storage tankiis receiving crude oil from the berthbduring slots. Similarly, the discharging operation must be in progress while the inventory of storage tankidecreases.Meanwhile,BOSTCTijsdenotes that the storage tankiis feeding crude oil to charging tankjduring slots. The storage tankican discharge oil to any charging tank,but upon considering the operability, this operation is limited to two charging tanks at most. The storage tankicannot discharge oil to any charging tank when it is receiving oil from any vessel and vice versa.Furthermore, it can receive crude oil from only one berth at the same time. Keeping the purity of crude oil in storage tanks is beneficial to controlling the quality of petroleum products and measuring the accurate unloading amount of crude oil.Therefore, the storage tankithat already contains a certain type of crude cannot receive other types of crude from any vessels.Binary variableBICSTicsin constraints(33) and (34) indicates whether it is possible for the storage tankito receive crude oilcduring slots.When the storage tankihas already stored crude oilc′(c′≠c)during time slots‐1, the itemVTSTi(s−1)−VCSTic(s−1)>0,and according to constraints (33) and (34), the variablesBICSTicsandVICSTicsmust be 0. The storage tankican only receive one type of crude oil at the same time. (2) Flow rate constraints The output of storage tanks should meet the transfer rate limits. (3) Brine settling operation constraints A storage tank after receiving crude oil must wait for several hours to settle and remove brine. (4) Material balance constraints (5) Capacity limits The inventory level of all storage tanks must respect the lower and upper limits of inventory. (1) Charging and discharging constraints The charging tankjcan receive crude oil from multiple storage tanks, the number of which should not exceed two. LetBOCTCDjdsbe the output status for the charging tankjto CDUdduring slots.The value of variablesBOCTCDjdsis determined by the crude volume between these two devices. A charging tank cannot be fed by any storage tank while it is transferring oil to any CDU and vice versa.In addition,it is assumed that there is a one‐to‐one connection between charging tanks and CDUs.Thus constraint (48)is formed. To avoid changes in feed quality and flow rate of CDUs,we stipulate that the charging tankjonly can stop feeding CDUduntil it is empty at the end of slots‐1 by constraint(49).Although optimization may be weakened, the constraint is still reasonable while considering the safety production as the first criterion. (2) Flow rate constraints The crude transfer amount from the charging tankjto CDUdshould match up to the minimum and maximum feeding rate of tankj. (3) Material balance constraints (4) The inventory level of charging tanks should be within the allowable inventory range. (5) Components concentration constraints The key components such as sulfur and specific gravity are critical to determine the crude oil property.Rigorous key component concentration constraints can only be nonlinear constraints, and they will slow down the calculating speed of our model.So we just use relaxation constraints to limit the concentration of key components in charging tanks within a suitable range. (1) Feeding constraints We assume one and only one charging tank can deliver oil to CDUdduring slots. It is necessary to meet the processing rate limits. (2) Changeovers of feed tanks Because of production fluctuations, it is not recommended to change the feed tank of CDUd, and we let a 0‒1 continuous variable to denote whether CDUdcan change the feed tank at the beginning of slots. (3) Crude demand The delivery of charging tankjis the planned demand of CDUs within the scheduling period. The objectives of the model are to maximize the processing potential of all CDUs and to minimize the departure times of the vessels and the feed changeovers of the CDUs. The first item of the objective function indicates that the charging tanks will receive as much low‐quality crude oil as possible.This not only can help to maximize the processing profit during the current scheduling period,but also can ensure that in the next period there will be enough crude oil suitable for production and enough empty storage tanks for fast unloading of vessels.The second item is to reduce the demurrage of vessels.The third item is to minimize the feed changeovers of CDUs to promote the stable production of the enterprise and reduce the workload of the personnel. As noted earlier, the charging tankjthat feeds CDUdduring the slots‐1 must continue to feed the same CDU at the slotsunless the tank is empty or the scheduling period terminates at the end of slots‐1.Therefore, the crude composition from charging tankjto CDUdmeets the processing requirements of the CDU as long as that composition in the tankjvaries within the lower and upper limits before the discharge operation begins.Constraints (54)‒(57) reflect the above characteristics,denoting that our model does provide a feasible crude oil schedule. Now, we focus on the accurate properties of crude oil in the charging tanks and the stable feed rate of the CDUs.Figure 2 shows the calculation process. Figure 2 Flow chart for obtaining the properties of mixed oil in charging tanks and CDUs feed rate We can get the values of variablesBOCTjs,BFOCTjs,NSLCTjs,VTOCTjsandCKCTjksaccording to the results of optimization model referred to in Section 3.The following pseudo code is proposed for the computing process, wheresolution(variablex) expresses the value of variablexobtained from the model results. When the charging tankjis idle or receiving oil from any storage tank, the total key component level in the tank is strictly determined by the constraints (56) and (57).In this case, we divide the total key component level by the total inventory level to get an accurate crude oil composition in the tankj.When the charging tankjfeeds one CDU, the crude composition in tankjis consistent with that measured before the crude is delivered. If CDUdreceives oil from the charging tankjduring time slotstos+NSLCTjs, the feed rate of CDUd, namelyFCDds, is equal toVTOCTjsdivided by (TESLs+NSLCTjs−TESLs−1).The method keeps the processing rate of CDUdconstant during time slotstos+NSLCTjs. We add the start time and end time of high tides based on the second and fourth examples introduced by Lee, et al.[1]Table 1 shows the tides information for the future 15 days, and additional details can be referred to theliterature [17]. Table 1 Duration of each high tide The scheduling model is developed in python language and implemented using the Gurobi solver on a personal computer with Intel i7‐4790 dual‐core 3.6GHz CPU and 4 GB RAM.We preset the number of time slots to 8,and Table 2 gives the model statistics and performance,respectively, for these cases. Table 2 Statistics of variables, constraints and calculation time Case 1 involves 3 storage tanks, 3 charging tanks, and 2 CDUs.This is a crude operation problem with a 10‐day scheduling period, during which 19 high tides will occur and 3 vessels will arrive.And two key components are used to characterize a type of crude oil.Figures 3 and 4 illustrate the crude schedule for example 1.By analyzing the data in these figures, we can obtain the following valuable features: (1) The docking and departure operations of all vessels occur during high tides (Figure 3).For instance, VL1 docks and departs on days 0.22 and 2.29 corresponding to the 1stand 5thhigh tides, respectively. (2) The unloading scheme enables vessels to unload crude oil at the maximum rate, which greatly reduces the possibility of demurrage.The unloading rate of VL1 is 48.34 Mbbl/d, which is lower than 50 Mbbl/d, however, it is optimal due to the influence of tides. (3) Our model is more flexible because of the hybrid continuous time representation.Our proposed time representation requires only 8 time slots, while the same crude oil schedule needs 12 synchronous time slots[25], as shown in Figure 3. (4) No composition discrepancy occurs during the scheduling horizon.For instance, in Figure 3 crude A(crude composition: 0.010, 0.040) in ST3 and crude B(crude composition: 0.030, 0.020) in ST2 are mixed into the vacant CT1 at a volume ratio of 1:1, and the crude composition (0.020, 0.030) in CT1 is consistent with the model’s calculation results given in Figure 1. (5) There are 3 feed changeovers of CDUs in Figure 3.These feed changes are necessary since the initial inventories of charging tanks (30, 50, and 30 units) are insufficient for meeting the processing demands (100, 100 and 100 units). (6) Figure 3 also exhibits other operational constraints mentioned in Section 3, such as, the charging and discharging operations of storage tanks should meet the settling time requirement.Take ST2 as an example, it finishes the receiving operations at day 8.01, and is then idle for 0.33 days and starts to discharge oil into CT3 at day 8.43. Case 2 is a factory‐level scheduling problem involving 6 storage tanks, 4 charging tanks and 3 CDUs.It is a long scheduling period (15 days), with 29 high tides and 3 vessels arriving.Figures 5 and 6 draw up the detailed operation schedule and tank inventory changes,respectively.This crude schedule exhibits the same characteristics as the schedule for case 1.Besides, Figure 6 shows that ST1 is empty and CT3 is full at the end of the scheduling period.The feature can respectively facilitate rapid unloading operations of vessels and can minimize changeovers of CDUs during the next scheduling period. Figure 3 Gantt chart of the optimized crude operation for example 1 Figure 4 Inventory profiles of each tank for example 1 Figure 5 Gantt chart of the optimized crude operation for example 2 Figure 6 Inventory profiles of ST1 and CT3 for example 2 Although crude scheduling problem has been studied formore than 20 years, the influence of tides on the vessels docking and departure is still not considered.We propose a new complete crude scheduling model on this problem,which also includes other practical operations, such as multi‐berth docking and brine settling.In our algorithm,a hybrid continuous time representation that integrates the global time grid and the specific‐unit time grid is established to combine the advantages of simplicity and flexibility.Crude blending may trigger nonlinear constraints.How to convert a MINLP model to a MILP or MILP‐NLP iterative model without composition discrepancy is a hot issue.We take a different approach and use reasonable model assumptions to solve this problem.The assumptions are that crude blending only occurs in the pipeline between storage tanks and charging tanks, and the discharging operations can only be endedwhen charging tanks are emptied.Two cases prove that our model can provide optimized crude schedule which achieves the shortest vessel demurrage and the least number of feed changeovers of distillation units.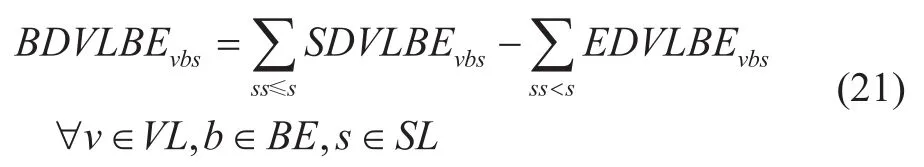



3.4 Berths realistic features


3.5 Storage tanks operations and inventory profiles










3.6 Charging tanks operations and inventory profile









3.7 CDU processing operations




3.8 Objective

4 Solution Algorithm




5 Examples


5.1 Example 1
5.2 Example 2



6 Conclusions




- 中国炼油与石油化工的其它文章
- Controlling the Pore Structure and Photocatalytic Performance of the Flexible FeⅢ Metal-Organic Framework MIL-53(Fe) by Using Surfactants
- Acidity Evaluation of Industrially Dealuminated Y Zeolite via Methylcyclohexane Transformation
- Study on Distribution of Electrocatalytic Reaction Efficiency in a Three-Dimensional Electrocatalytic Reactor
- Preparation of Ultra-High Molecular Weight Polypropylene Using Ziegler-Natta Catalyst via Combining Internal Electron Donor and Cocatalyst Loading
- Preparation of Modified Enteromorpha-Immobilized Microbial Agent and Research on Diesel Removal Performance
- Chemoselective Catalytic Hydrogenation of Nitroarenes Using MOF-Derived Graphitic Carbon Layers Encapsulated Ni Catalysts

