尺度自适应的离散统一气体动理学格式

许 丁 刘 欣 孙 祥

(1. 西安交通大学航天航空学院 机械结构强度与振动国家重点实验室，西安 710049;2. 陕西省先进飞行器服役环境与控制重点实验室，西安 710049)

1 引言

随着人们对多尺度流动问题的深入研究，传统基于连续介质假设求解Navier-Stokes 方程的方法显示出更多的局限性，而基于气体动理学理论的方法所具有的优势则更多的被人们重视.气体动理学从微观角度出发，引入气体速度分布函数的概念并建立其满足的Boltzmann 方程.目前基于Boltzmann 方程的气体动理学格式应运而生，如格子Boltzmann 方法(Lattice Boltzmann Method, LBM)[1-3]、气体动理学格式(Gas Kinetic Scheme, GKS)[4,5]、统一气体动理学格式(Unified Gas Kinetic Scheme, UGKS)[6,7]、离散统一气体动理学格式(Discrete Unified Gas Kinetic Scheme,DUGKS)[8,9]等.这些方法与基于Navier-Stokes 方程的求解方法相比，可以获得更多的流动信息，目前已取得众多成功应用[10-16].但是，这些动理学方法又各有一些局限与不足.例如，LBM 作为一种有限差分方法对低速不可压缩流动问题有着很好的适用性，但其对均匀网格的需求限制了其在高Re数下边界层流动问题中的应用.GKS 作为一种有限体积方法，定位于求解传统Navier-Stokes 方程，不能应用于连续介质假设失效的较大Kn 数流动.UGKS 方法是一种适用于多尺度流动问题的统一方法，在处理多尺度复杂流动中取得了较好的结果，但该方法要同时追踪宏观守恒量和分布函数，并要计算平衡态分布函数在界面处的空间导数和时间导数从而涉及大量矩阵运算，计算成本较高.DUGKS 方法沿特征线离散Boltzmann 方程，可认为是UGKS 方法的一种简化形式，相比UGKS 来说DUGKS 计算中只需追踪分布函数，且不再需要计算平衡态分布函数的时空导数，降低了计算开销.但是DUGKS 在处理碰撞项时采用碰撞项的显式处理和隐式处理的算术平均，这种处理方法主要基于数值的角度，未曾从物理上深入考虑两个时间尺度即计算时间步长和碰撞松弛时间之间的相对大小对粒子碰撞过程宏观表现的影响.

本文在原始DUGKS 基础上，将碰撞项的处理改成显式和隐式的加权平均，其中权系数依赖于当地碰撞松弛时间和计算时间步长之比，即当地Kn 数.通过数学和物理上的分析发现，该权系数可以根据当地Kn 数做出自适应调节，从而使所得方法具有尺度自适应特性，适用于所有Kn 数下的流动.

2 Boltzmann-BGK 模型方程沿特征线离散的一般形式

碰撞项采用BGK 模型的Boltzmann 方程如下

其中f=f(xi,t,uj)为t时刻、位置xi处、速度为uj的粒子速度分布函数，τ为碰撞松弛时间，g为平衡态分布函数

其中ρ为流体密度，R为气体常数，T为温度，D为空间维度，Ui为宏观速度.宏观量可以通过分布函数取矩得到，如对于二维等温流动问题

其中dΞ = dudv, ψ= (1,u,v)T为碰撞不变量.根据粒子碰撞过程满足质量与动量守恒定律，碰撞项需在任意时刻、任意空间位置满足如下相容关系

对于Boltzmann-BGK 方程，若松弛时间τ为常数，则t+s时刻的分布函数可形式上写为[4]

其中t为初始时刻，s为时间发展长度，x′i=xi-ui(s-t′)为粒子运动轨迹，fini(xi-uj) =f(xi,t,uj)代表初始时刻t的非平衡态分布函数.尽管Boltzmann-BGK 方程(1)基于微观观点建立，其所蕴含的流动尺度却不限于微观动理学尺度，这一点可以从式(5)清楚看出：式(5)右边第一项积分项反映粒子之间相互大量碰撞作用的积累效果，该项已被证明可以看作为宏观连续流动动力学模型[17]，对应为宏观动力学尺度；式(5)右边第二项反映粒子的迁移运动，对应微观动理学尺度.式(5)将宏观动力学尺度和微观动理学尺度有机地结合到一起，可以很好反映多尺度流动特性.但是式(5)并不能直接使用，因为右边第一项涉及积分的平衡态g是未知的，需要满足相容关系式(4).因此从这个角度上来说式(5)只是式(1)形式上的解.

另一方面，认识到Boltzmann-BGK 方程(1)自身已将宏观动力学尺度和微观动理学尺度有机地结合到一起，因此可以直接从Boltzmann-BGK 方程(1)出发来构造多尺度计算格式.这里将(1)式沿特征线进行离散，可得到

其中gini(xi,uj) =g(xi,t,uj)和Ωini(xi,uj) = Ω(xi,t,uj)分别代表初始时刻t的平衡态分布函数和碰撞项.上式(6)右端的碰撞项采用了显式和隐式加权平均处理.α为隐式部分对应的权系数，其为碰撞松弛时间τ和时间发展长度s的比值τ/s的函数，具体形式待定.上式(6)可整理为

式(7)为Boltzmann-BGK 方程沿特征线离散的一般形式，其右端前两项和平衡态分布函数相关反映粒子之间的碰撞作用，和式(5)右端第一项积分项对应；式(7)右端第三项和初始非平衡态分布函数相关反映粒子的迁移效应并和式(5)右端第二项相对应.通过对比式(5)和式(7)中的非平衡态分布函数相关项，并令ϑ3=e-s/τ，可确定权系数α为

由上式(9)可以清楚看出权系数α数学上直接依赖于时间比值τ/s，物理上的讨论将在后面第4 节给出.确定了α后将其带入到(8)式，可得系数ϑ1, ϑ2和ϑ3具体形式

为了进一步分析式(7)的数学物理特性，这里将从两种极限流动的角度来讨论，首先将其整理为以下形式

对于Kn→0 的宏观连续流动问题，物理上理解为在一个时间步长内粒子经历的碰撞次数足够多，即τ ≪s，此时数学上给出β1→0, β2→τ/s，从而(11)式可化为

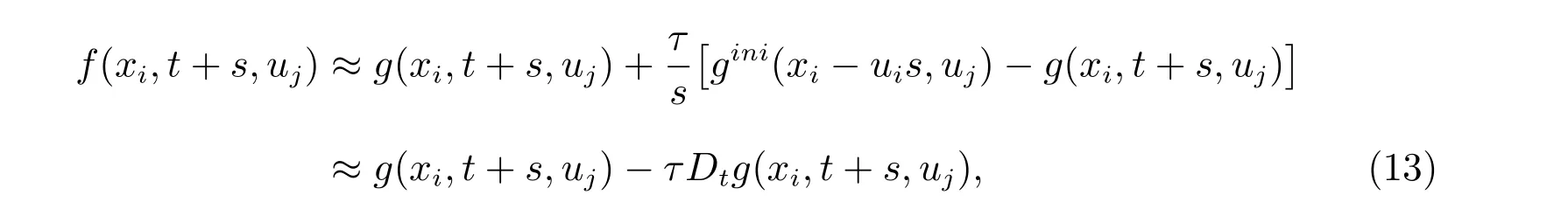
其中Dt=∂t+uj∂xj.众所周知，当对Boltzmann-BGK 方程(1)进行Chapman-Enskog展开至O(τ)阶时也得到(13)式[4]，其对应宏观方程为Navier-Stokes 方程.由此说明在宏观连续流动区域式(7)对应为Navier-Stokes 方程，此时流动尺度为宏观动力学长度和时间尺度.

另一方面，对于Kn≫0 的稀薄流动或微尺度流动问题，有τ ≫s，此时数学上给出β1→1, β2→1，从而(11)式化为

上式是自由分子流运动的解，此时流动对应微观动理学尺度，长度尺度为分子平均自由程尺度，时间尺度为碰撞松弛时间尺度.

由上述分析可知，Boltzmann-BGK 方程沿特征线离散的一般形式(7)将宏观动力学尺度和微观动理学尺度有机地结合到一起，其中引入的系数ϑ1, ϑ2和ϑ3依赖于比值τ/s且可根据当地流动状态的不同进行自适应调节，两个时间尺度即碰撞松弛时间尺度和时间步长的比值τ/s在调节中起到了关键作用.

3 尺度自适应的离散统一气体动理学格式

本文在文献现有离散统一气体动理学格式DUGKS[8]基础上发展出具有尺度自适应特性的离散统一气体动理学格式(Scale Adaptive Discrete Unified Gas Kinetic Scheme,SADUGKS).二者主要差别体现在碰撞项的处理不同，在DUGKS 中碰撞项采用算术平均，权系数恒为常数αDUGKS≡1/2；而在SADUGKS 中，碰撞项采用加权平均处理，权系数由式(9)给出，可根据当地流动状态的不同进行自适应调节.

将Boltzmann-BGK 方程(1)在网格单元Vj及时间步长(tn,tn+Δt)内积分，得

对式(15)中通量的时间积分项采用中点公式处理

对式(15)中碰撞项的时间积分采用加权梯形公式

其中α(Δt)为式(9)给出的权系数

将式(17)和式(18)代入到式(15)中，可得

从式(20)可以看出该式右端包含了碰撞项和通量的隐式部分，因此，在使用该式进行迭代递推之前必须先解决碰撞项和通量的隐式离散问题，下面对其分别进行处理.

其中t=tn为初始时刻，时间发展长度为r= Δt/2, xi,b为第m个网格单元界面位置，α(r)由式(9)给出.引入辅助分布函数¯f定义

上式也等价于

接下来，处理碰撞项中的隐式部分Ωn+1，引入新的辅助分布函数～f定义如下

由相容关系式(4)同时结合定义式(30)可知

将式(30)代入到式(20)，整理得

再次指出的是在原始DUGKS 格式中，从式(20)至(26)，式(30)和(32)中出现的所有权系数α恒取为αDUGKS≡1/2，而SADUGKS 中权系数形式由式(9)给出.

需要说明的是上述在推导SADUGKS 时速度空间是连续的，实际在使用SADUGKS 时还需将速度空间离散，其离散方法与DUGKS 格式[8]相同.

关于边界条件的处理分两类，针对宏观连续流动问题，SADUGKS 格式在固体壁面处采用了无滑移边界条件；而对大Kn 数流动问题，则采用了完全漫反射边界条件，具体实现与DUGKS 格式[8]相同，亦不再赘述.

4 尺度自适应的离散统一气体动理学格式的性质讨论

首先，SADUGKS 格式基于DUGKS 格式发展出来，SADUGKS 格式同样具有渐近保持性[8,18]，这一点可以清楚地从式(13)看出.

其次，SADUGKS 格式具有尺度自适应特性，能够根据当地流动状态不同进行自适应调节.SADUGKS 格式中，时间步长选取按照CFL 条件确定

其中Δ 为空间计算网格尺度，CFL 为CFL 数；|u|max为粒子最大离散速度，通常与声速c同量级.

同时，碰撞松弛时间τ可近似为

式中ls为分子平均自由程，¯u为粒子平均运动速率与声速c同量级.因此可以得到

其中Kn 为当地努森数，反映当地的流动状态和流动尺度.在SADUGKS 格式中，用来计算界面通量的式(21)和碰撞项加权离散的式(18)中皆出现权系数α，而权系数α依赖于比值τ/Δt，即依赖于当地Kn 数，因此，α取值的大小会随着当地流动状态和尺度的不同而改变.

众所周知Boltzmann-BGK 模型将气体从当前非平衡状态向平衡态的过渡看作为一个驰豫过程.对于Kn→0 的宏观连续流动问题，从物理上分析，此时碰撞弛豫时间远小于时间步长，τ ≪Δt，即在一个时间步长Δt内粒子经历足够多次的碰撞，因此弛豫过程受初始时刻碰撞项Ωini(xi-uiΔt,uj)的影响很小，即粒子的碰撞历史效应可忽略，当前的分布函数f(xi,t+Δt,uj)将只决定于当前的碰撞Ω(xi,t+Δt,uj)；而另一方面，从式(6)的数学表达上分析，此时α →1，式(6)简化为

可见数学结果与上述物理分析一致.

对于Kn≫0 的稀薄流动或微尺度流动问题，从物理上分析，碰撞弛豫时间远大于时间步长，τ ≫Δt，即在一个时间步长Δt内粒子几乎不发生碰撞，从而每次发生的碰撞都对当前的分布函数f(xi,t+ Δt,uj)有着至关重要的影响，因此初始碰撞作用Ωini(xi-uiΔt,uj)和当前碰撞作用Ω(xi,t+Δt,uj)都要保留.另一方面，从数学上来看，此时α →1/2，式(6)可简化为

可见此时数学结果也与上述物理分析相一致.

根据上述分析可知，式(9)给出的权系数α紧密依赖于时间比值τ/Δt，并可根据当地流动状态和流动尺度的不同进行自适应调节，因此SADUGKS 是一种尺度自适应的格式，适用于从连续流动到滑移流动、过渡流动及自由分子流所有流动问题，在第5 节中该格式的应用也很好地体现出了这一点.

5 在低速不可压缩流动问题中的应用

5.1 二维非定常Taylor 涡问题

为了验证SADUGKS 格式的空间精度，本文对二维非定常Taylor 涡问题[8]进行模拟.该问题的解析解如下所示其中，平衡态分布函数g可用式(39)由初始解析解得到；边界条件采用周期性边界条件.离散速度及权系数由3 点Gauss-Hermite 公式[8]决定.

为分析格式的空间精度，本文采用了一系列不同数量(N×N)的均匀网格；为了消除时间步长对误差的影响，在计算中将时间步长设置为固定小量(Δt= 2τ).统计在tc=ln(2)/(8νπ2)时刻流场速度的误差L2, L2定义为

其中U 和Ue分别指数值解速度和解析解速度.

采用64×64 均匀网格得到的不同时刻的速度剖面，如图1 所示，可以看到SADUGKS格式得到的数值解与解析解能够很好地吻合，证明了SADUGKS 格式对于Taylor 涡问题的适用性；表1 展示了在tc时刻网格量与误差的关系，从中可以看出SADUGKS 格式具有空间2 阶精度.

表1 SADUGKS 格式模拟Taylor 涡问题时的误差与空间精度

图1 SADUGKS 格式模拟Taylor 涡问题不同时刻的速度剖面(64×64 均匀网格)

5.2 宏观连续流动下方腔驱动流问题

二维方腔驱动流问题为计算流体力学中验证数值算法的经典算例，随着雷诺数变化，流动结构及旋涡等也随之改变，因此能够很好地验证算法的粘性分辨率及旋涡捕捉能力.为了验证SADUGKS 格式，本节对宏观连续流动下的二维方腔驱动流问题进行了数值模拟，并与文献[19]的结果以及LBM 方法的计算结果进行了对比.

方腔边长为L，上边界以U的速度匀速运动，其余边界静止，流动雷诺数为Re=UL/ν，其中ν为运动学粘性系数.本节在计算中，令L= 1.0, U= 0.1, RT= 1/3，故流动马赫数较小，流动可作为不可压缩流动.CFL 设置为0.5，离散速度及权系数由3 点Gauss-Hermite 公式[8]决定，以保证与LBM 采用的D2Q9 格子模型一致.LBM 方法中所有速度边界均采用非平衡态外推边界条件[20]，SADUGKS 格式中所有边界均采用无滑移边界条件[8].

雷诺数Re= 1000 时，不同计算网格下沿方腔中线的速度剖面，如图2 所示.从图2 左图可知，在采用相同的50× 50 均匀网格的条件下，SADUGKS 格式得到了比LBM 方法更好的结果，特别是下壁面附近优势更为明显，表明SADUGKS 格式对壁面附近粘性边界层的分辨较好.此外，作为一种有限体积格式，SADUGKS 格式可以使用非均匀网格，通过在壁面处进行加密来进一步减小计算误差及所需网格量.图2 右图展示了SADUGKS 格式采用在壁面处进行局部加密的30×30 非均匀网格、LBM 方法采用100×100 均匀网格的结果对比，可以看出两种方法得到的结果都与文献[19]的结果吻合较好.

图2 方腔驱动流Re=1000 时SADUGKS 与LBM 结果对比

此外，本文采用SADUGKS 格式计算了更高雷诺数的方腔驱动流，以检验SADUGKS格式对高雷诺数流动中旋涡的捕捉能力及格式的稳定性.采用30×30 均匀网格、与图2 左图中相同的30×30 非均匀网格及加密后的50×50 非均匀网格等三种网格，雷诺数选择为Re= 3200,5000,7500 和10000，计算结果如图3 所示.可以看出SADUGKS 格式的结果总体上与文献[19]的结果吻合较好，且随着网格不断加密，速度峰值的捕捉更加精确，50×50 非均匀网格足以很好地反映高雷诺数下的流动状态.在稳定性方面，可以看到即使采用较为稀疏的30×30 的均匀网格，SADUGKS 格式也能够对上述所有高Re数流动得到物理上合理的结果，说明该格式具有较好的稳定性.

图3 不同网格不同Re 数下，SADUGKS 计算方腔驱动流所得速度剖面

最后，分别使用DUGKS 和SADUGKS 格式计算了雷诺数为Re=3200,5000,7500和10000 的方腔驱动流，为了消除非均匀网格带来的影响，这里采用50×50 的均匀网格，两种格式计算时边界条件设置和CFL 数取法相同，两种格式的计算结果见图4.可以看出从整体上来说SADUGKS 和DUGKS 所得结果均与文献[19]的结果吻合较好，但是在局部点如速度极值点附近，SADUGKS 与文献[19]的结果更为贴近，并且随着Re的增加，DUGKS 在极值点附近和文献[19]的结果偏差增大.

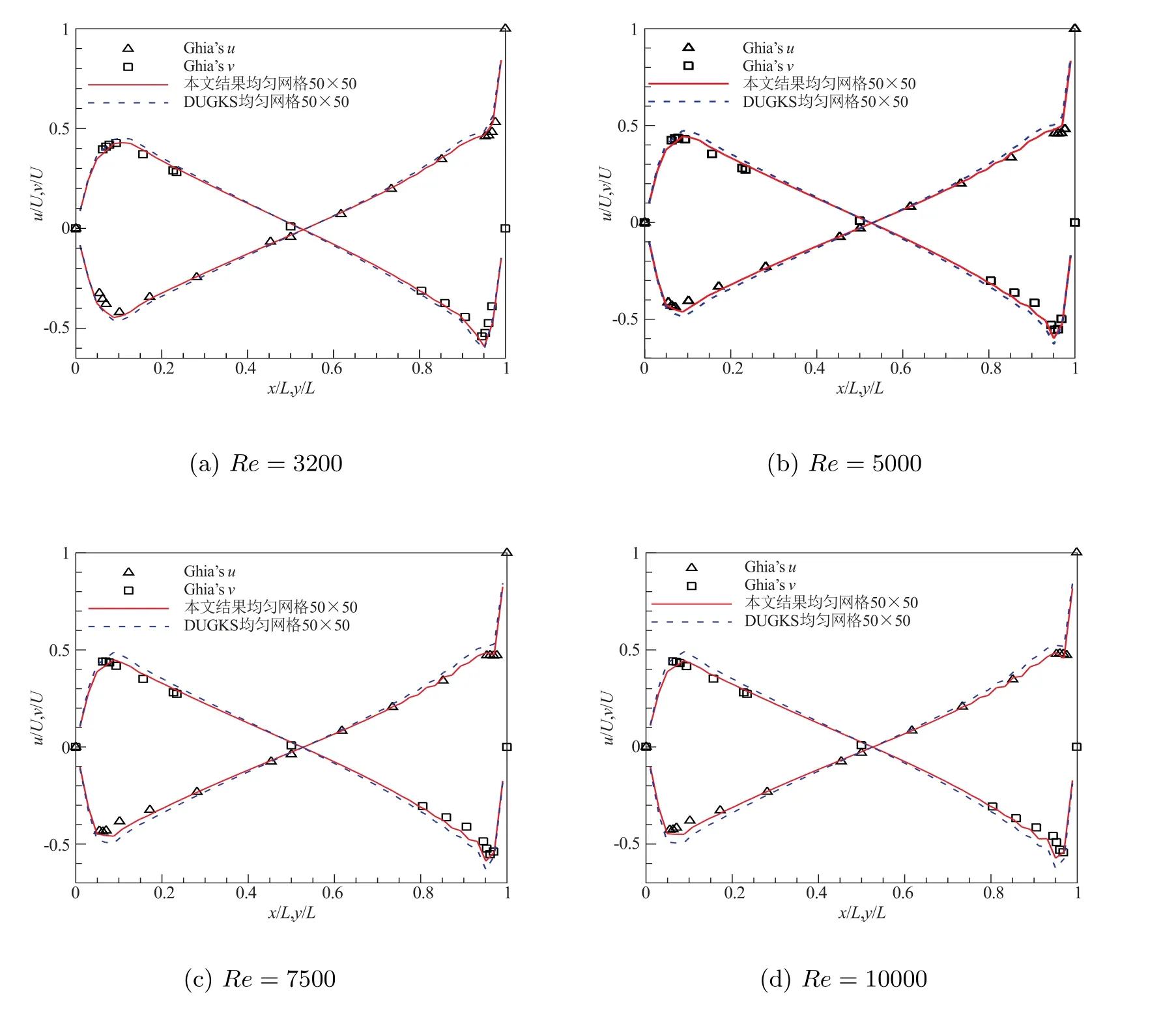
图4 不同Re 数下DUGKS 和SADUGKS 计算方腔驱动流所得速度剖面

5.3 宏观连续流动下后台阶流动问题

另一个经典宏观连续流动问题是后台阶流动问题，流动过程中包含有流动分离与再附.本节对后台阶流动进行了数值模拟，并与文献[21]中的实验结果进行对比.流动示意图见图5 所示，坐标原点取在台阶处.

图5 后台阶流动区域示意图

来流入口速度为抛物线分布

其中Umax为最大速度.在后台阶流动中，雷诺数定义为Re= (H-h)Umax/ν.本文计算中取Umax= 0.1, l= 4.0, H= 3.0, h= 2.0, L足够长(L= 35)以保证出口处流动充分发展，可采用非平衡态外推边界条件[20]；台阶及上壁面处均采用无滑移边界条件[8].本文采用均匀网格(250×100)，数值模拟了Re= 50 及Re= 150 的后台阶流动.图6 和图7 分别给出了Re=50 及Re=150 在四个不同位置处的水平速度剖面结果.

从图6 中可以看出，Re= 50 的流动在x= 1.5 处出现了回流，说明流动经过后台阶发生流动分离，产生了旋涡；在台阶下游处，随着x逐渐增大，速度逐渐发展为抛物线分布，表明台阶的影响逐渐减弱.图7 显示了相似的变化规律.此外，Re= 150 时，在x= 4.0 处仍然存在回流，表明随着Re增加，粘性降低，旋涡的尺寸逐渐增大.在上述两种不同Re下，SADUGKS 格式得到的数值结果均能与实验结果较好地吻合，再次说明SADUGKS 格式对粘性流动分离、再附及旋涡具有较好的捕捉能力.

图6 后台阶流动不同位置处的速度剖面图，SADUGKS 所得结果与实验结果的对比

图7 后台阶流动不同位置处的速度剖面图，SADUGKS 所得结果与实验结果的对比

5.4 不同Kn 数下的等温Couette 流动问题

本节中将SADUGKS 格式用于求解不同Kn 数下等温Couette 流动，以验证格式对大Kn 数问题的适用性.流动描述如下：两无限大平板互相平行，距离H，之间充满静止流体，上下板分别以Uw和-Uw的速度沿水平方向反向运动，由于壁面处的粘性剪切作用，板间流体会运动并最终达到稳定状态.这一问题已被诸多学者用包括DSMC[22]、UGKS[7]及DUGKS[8]在内的多种方法研究过，可以很好地检验格式求解大Kn 数问题的正确性及粘性剪切力的计算.

本文中，物理空间在竖直方向采用40 个均匀网格进行离散，速度空间采用28×28 半平面Gauss-Hermite[8,23]积分离散.入口与出口采用周期性边界条件，上下壁面采用完全漫反射边界条件[8].研究了多个不同Kn 数下的流动，并与文献[22]结果及文献[24]利用线性化Boltzmann 方程LBE 计算所得的结果进行对比.

三种方法所得不同Kn 数下的速度剖面，如图8(a)所示，由于流动的对称性，图中只给出了流场的上半部分.从图中可以看出，在所有Kn 数下，SADUGKS 格式的结果与其他方法均能很好地吻合，且随着Kn 数不断增大，壁面处的速度滑移效应也越来越显著，三种方法均能很好地反映出大Kn 数流动下的速度滑移效应.图8(b)所示为壁面处的切应力τw随Kn 数的变化曲线，考虑到较大Kn 数下连续介质假设不成立及牛顿粘性切应力公式失效，图中壁面切应力采用气体动理学理论计算，即

图8 SADUGKS 格式计算不同Kn 数(k =Kn/2)下的Couette 流动

6 结论

本文首先提出了Boltzmann 方程沿特征线离散的一般形式，在该式中碰撞项的离散采用了显式和隐式加权平均的方法，其中权系数α依赖于当地碰撞松弛时间和计算时间步长的比值.同时基于该式，在文献现有离散统一气体动理学格式(DUGKS)基础上提出了具有尺度自适应的离散统一气体动理学格式(SADUGKS).接下来，本文对SADUGKS 格式的尺度自适应特性进行了讨论，发现在SADUGKS 格式中，权系数α与反映当地流动尺度的当地努森数Kn 直接相关，当流动尺度发生变化时，α随之变化，使得SADUGKS 格式能够进行自适应调节，因此可以处理从宏观连续流动到自由分子流的多尺度流动问题.最后，本文将SADUGKS 格式应用到若干低速不可压缩流动问题中，通过这些经典算例对该格式进行了检验.计算结果表明：基于有限体积法的SADUGKS 在网格选用上更加灵活，格式稳定性较好，对高Re数下的流动边界层具有较高的分辨能力；对于流动分离、再附和旋涡也有较好的捕捉能力；此外，能够很好地描述从小Kn 数的宏观连续流动一直到大Kn 数的自由分子流动.

目前使用SADUGKS 仅在若干经典低速不可压缩流动算例中进行了验证，后续工作将在更加复杂的多尺度流动中进一步进行检验.另一方面，本文的研究基于Boltzmann-BGK 模型方程，结果仅适用于低速不可压缩流动，后续将尝试将SADUGKS 推广到Boltzmann-Shakhov 模型方程中，并应用于非等温、高速可压缩流动及伴有间断现象的复杂流动中去.