基于不同边界条件下微分矩阵的特征分解

霍俊蓉，张荣培，温学兵

（1. 沈阳师范大学 数学与系统科学学院，沈阳 110034；2. 广东工业大学 应用数学学院，广州 510006）

0 引言

近年来，许多学者采用有限差分方法对逼近多种模型方程进行了研究，包括Allen-Cahn方程［1］，Cahn-Hilliard方程［2］，反应扩散方程［3］，薛定谔方程［4］等等. 这些方程在物理、化学、化工、材料科学［5-8］等方面有越来越广泛的应用. 在数值分析中，计算矩阵的特征值与特征向量是一项主要研究内容，也是求解矩阵的重点. 应用有限差分方法离散数值方程时，将得到方程的微分矩阵，在大多数情况下，需结合微分矩阵的特征值与特征向量对其进行特征分解，进而得到对角矩阵，使得计算更加简便快捷. 本文总结了微分矩阵的特征分解形式，并通过求解其特征值与特征向量来验证三种不同边界条件下的分解形式.

1 微分矩阵的特征分解

设有三种不同边界条件，即齐次Neumann边界，Dirichlet边界，周期边界. 利用二阶中心差分方法对模型方程进行离散，可以得到方程在网格节点处的二阶导数差分格式. 定义常数ε1，ε2，方程在三种边界条件下对应的N×N阶微分矩阵分别为A，B，C. 其中（A）ii=（B）ii=（C）ii= 2，i= 2 ，…，N-1，Aii-1=Bii-1=Cii-1-1，i= 2 ，…，N，Aii+1=Bii+1=Cii+1=-1，i= 1 ，…，N-1，A1，1=AN，N= 1，Bii-1=BN，N=C1，1=CN，N= 2，C1，N=CN，1=-1，矩阵A，B，C中其他位置的元素均为0.

考虑如下特征值问题：

其中λ为特征方程的特征值；v为相应的特征函数；由于微分矩阵是由二阶导数差分后离散得到，因此可以考虑v在离散点的值作为矩阵的特征向量，记为y.

1.1 齐次Neumann 边界

首先，设定边界条件为齐次Neumann边界，即

将求解区域等距划分为N个网格，其中步长为hA= 1N，网格节点为xi= (i- 1 2)hA，i= 1，2，…，N，为了证明边界处的二阶精度，由网格中心点的定义，在边界左右各增加一个虚拟网格，其中心点坐标分别为x0= -1 2hA，xN+1= 1+1 2hA，下面求解其对应的特征值与特征向量. 求解（1）式对应的特征方程，即

(i) 当λA≤0时，根据对应的特征方程的通解，由条件（2），可得v=ε1，求得特征值λA= 0.

(ii) 当λA> 0 时，特征方程通解为，由条件（2），可得特征值=(mπ)2，m= 0，1，…，N- 1，相应的特征函数v= cos(mπx)，当m= 0时，λ0A= 0，v=ε1，此时包含(i)中结果.

矩阵A的特征向量为ym= (cosmπx1，…，cosmπxN)T，m= 0，1，…，N- 1，下面将矩阵A进行对角化，根据三角函数的和差化积公式，得到：

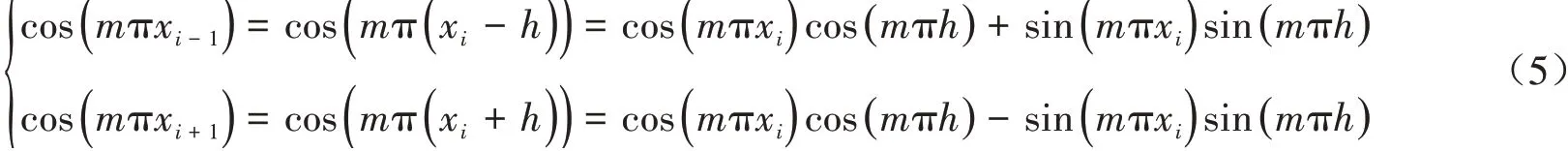
进而可将内部网格点的差分格式表示为：

由于cos(mπx0)= cos(mπx1)，cos(mπxN)= cos(mπxN+1)，因此可将边界网格点差分格式表示为：

结合（6）式及（7）式可以得到A=PA ΛAPA-1，其中矩阵PA=(y0，y1，…，yN-1)，对角矩阵ΛA=diag(2-2cosmπh).

（三）寄生虫性腹泻 主要由球虫、蛔虫、锥虫引起的腹泻较为多见，发生于20日龄以上的猪只，通常呈慢性经过，伴有食欲不振、咳嗽、呼吸困难、贫血等症状，有的腹泻与便秘交替出现，或伴有体温略升高，病猪因发育不良、瘦弱、衰竭死亡或变成“僵猪”。

1.2 Dirichlet 边界

设定边界条件为Dirichlet边界，即

将求解区域等距划分为N+1个网格，其中步长为hB= 1（N+1），网格点坐标为xj=jhB，j= 1，2，…，N，左右边界点坐标分别为x0= 0，xN+1= 1，下面求解其对应的特征值与特征向量. 求解（1）式对应的特征方程，即

(i) 当λA≤0时，根据对应的特征方程的通解，由条件（8），可得v≡0，无法求得特征值.

(ii)当λB> 0时，特征方程通解为，由条件（8）可得特征值m= 1，2，…，N，相应的特征函数v= sin(mπx).

矩阵B的特征向量为下面将矩阵B进行对角化，根据三角函数的和差化积公式，得到：

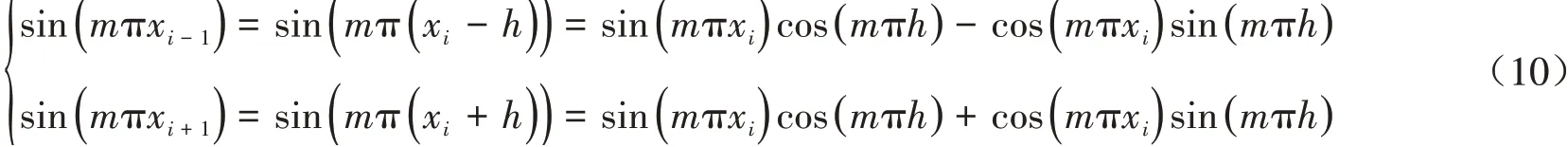
进而可将内部网格点的差分格式表示为

其中矩阵PB=(y1，y2，…，yN)，对角矩阵ΛB= diag(2 - 2cosmπh).

1.3 周期边界

设定边界条件为周期边界，即

将求解区域划分为N个网格，则步长为hC= 1N，内部网格坐标为xi=khC，k= 1，2，…，N- 1，其左右边界点坐标分别为x0= 0，xN= 1，下面求解其对应的特征值与特征向量. 求解（1）式对应的特征方程，即

(i)当λC< 0时，特征方程通解为，由条件（13），可得

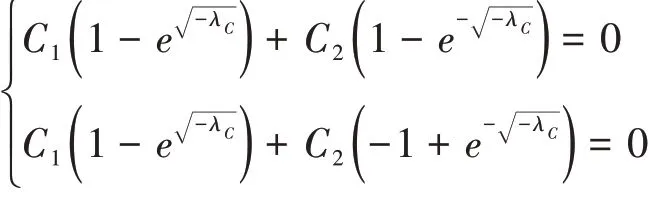
(ii) 当λC= 0时，特征方程通解为v=ε1+ε2x，由条件（13），可得v≡ε1，特征值λA= 0.

(iii)当λC> 0时，特征方程通解为由条件（13）可得

矩阵C的特征向量为，下面将矩阵C进行对角化，假设ε1= 0，ε2= 1，此时特征函数为v=e-i2mπx，可将内部网格点的差分格式表示为：

由于xN-1= 1 -x1，则有cos2mπx1= cos2mπxN-1，进而可以将边界网格点的差分格式表示为：

结合（16）式及（17）式可以得到：

其中矩阵PC= (y0，y1，…，yN-1)，对角矩阵ΛC= diag(2 - 2cos2mπh).

2 总结

本文在三种不同边界条件下，通过求解微分矩阵的特征值与特征向量，总结有限差分法离散二阶导数方程后得到的微分矩阵的特征分解形式. 将微分矩阵表示为由其特征值和特征向量表示的矩阵之积，其中包含对角矩阵，可以有效地提高求解非线性常微分方程组的速度与效率.