4-正则图中的不连通2-因子

胡 琳

(新疆大学 数学与系统科学学院， 新疆 乌鲁木齐 830017)

0 引言

本文中我们只考虑有限的无向简单图,对于未定义的符号与术语请参见文献[1].令G=(V,E)是一个图，顶点数记为|V|.对于任意顶点v∈V(G),用N(v)表示其邻点集合，即{u:uv∈E(G)}.v的度dG(v)(或简记为d(v))是指在G中与v相邻的边的条数.由于G是一个简单图，故d(v)=|N(v)|.集合S⊆V的开邻集即N(S)=∪v∈SN(v).G中的最小度与最大度分别用δ(G)和Δ(G)来表示.一个图称为k-正则的，如果Δ(G)=δ(G)=k.特别地，3-正则图也被称为立方图.此外，如果Δ(G)≤3,我们称G是准立方图.用c(G)表示图G的分支个数.

若V(G)=X∪Y,这里X∩Y=∅,|X|=m,|Y|=n,且∀e∈E(G),有e=xy,其中x∈X,y∈Y,我们称这类图为二部图，记为G=(X,Y;E).特别地，若X中的任一顶点与Y中任一顶点均有唯一的边相邻，则G为完全二部图，记为Km,n,当m=1时，称为n-star.如果图G中不含有同构于K1,3的导出子图，则称图G是无爪图，也称图K1,3是G的禁止子图.

如果V(H)=V(G),G的子图H称为生成子图.特别地，若H是G的生成子图且对于任意v∈V(H)均有dH(v)≥1,则H是G的一个因子.设f是定义在V(G)上的正整数值函数，若因子H中任一点v,均有dH(v)=f(v),则称H是G的一个f-因子.特别地，f的值均为偶数的生成子图称为G的一个偶因子.若偶因子中顶点度均为2，则是G的一个2-因子.集合S⊆V(G),G[S]定义为以S为顶点集合，其中两点相邻当且仅当它们在G中相邻的图.

称对G进行若干次删点、删边和缩边后所得的图H是G的一个minor.

下面是Petersen的一个经典定理[2].

定理1每个2r-正则图可以分解为r个边不相交的2-因子；每个无割边的立方图都包含一个完美匹配.

Tutte定理刻画了一类具有完美匹配或f-因子的图.Edmonds[3]第一次给出了图中寻找最大匹配的多项式时间算法，它也适用于寻找2-因子或f-因子.

李学良等[4]给出了不含有偶因子的图.

定理2令G是连通图，若G不包含偶因子，则存在子集S⊆V(G),使得

(i)S是独立集；

(iii)G-S的每个分支C,连接C与S的边数是奇数.

与此同时，他们还证明了下面的推论.

推论1若G是至多包含两个2度点，其余点度数至少是3的2-边连通图，则其包含一个偶因子.

通过给出的线图中的禁止子图[5]，康丽英等[6-7]得到了下面结论.

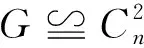
Funk等[8]最早提出，称一个图G是2-因子Hamiltonian的，如果其每个2-因子都是Hamilton圈.

定理4设G是2-因子Hamiltonian的k-正则二部图，则k≤3.

Diwan[9]证明了一个平面多重立方图G是2-因子Hamiltonian的，当且仅当或者G≌K4或者G与三条平行边连接两个顶点的图同构.Abreu等[10]提出了至今依旧未解决的下面这个有趣的猜想.

猜想1 一个4-正则图是2-因子Hamiltonian的，当且仅当G≌K5.

本文中，我们将证明上述猜想对于包含一个K4的无爪4-正则图成立.

1 预备工作

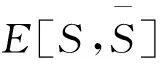
众所周知，对于任意图G,有κ(G)≤κ′(G)≤δ(G),并且若Δ(G)≤3,则κ(G)=κ′(G).

引理1G是连通的立方图，v∈V(H).如果κ′(H-v)=2并且H-v不包含2-因子，则在H-v中存在一个独立集S,使得

(i)c(H-v-S)=|S|-1,并且e(C,S)=3对G-S的每个分支C均成立；

(ii)NH(v)⊆S.

证明令H′=H-v.由于H′中不含有偶因子，由定理2，H′中存在独立集S,满足

(ii)对H′-S的每个分支C'都有eH′(C',S) 是奇数.

设V2是H′中度为2的点的集合，即V2=NH(v).另一方面，我们有

(1)

另一方面

(2)

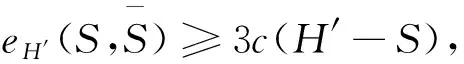
立方图中去掉一个顶点的图称为近似立方图.由定义，一个近似立方图是恰含三个2度点的子立方图.

推论2设H是3-连通立方图，V∈V(H).如果H-v不包含同构于二部立方图去掉一个顶点的minor，则H-v包含一个2-因子.

证明假设H-v不含2-因子.因为H-v是2-连通的，由引理1,存在H-v的独立集S满足

(i)H-v-S中恰有|S|-1个分支，并且对G-S的每个分支C均有e(C,S)=3；

(ii)NH(v)⊆S.

通过对H-v-S的每个非平凡分支C的收缩，我们可以得到一个二部立方图H′去掉一个顶点，矛盾.因此H-v包含一个2-因子.

推论3任意3-连通立方图G与其中一顶点v∈V(G),G-v可以被分解成一些3-star与一些包含2-因子的2-连通近似立方图的并.

证明此证明对G的顶点数n做归纳.当n=4,则G≌K4,从而G-v≌K3,显然G-v本身是一个2-因子.

假设n≥6,且结论对于所有顶点个数小于n的3-连通立方图和每个顶点v∈V(G)均成立.我们进一步假设G-v本身不含有2-因子,也就是说，由于Δ(G-v)≤3,它不包含偶因子.由引理1，G-v中存在一个独立集，使得

(i)G-v-S恰含|S|-1个分支, 对G-S的每个分支C都有e(C,S)=3；

(ii)V2⊆S.

根据以上讨论，我们选取满足条件且|S|最大的集合S.由(i)可知G-v-S的每个非平凡分支C是一个近似立方图.又G是3-连通的，故G-v-S的每个非平凡分支C一定是2-连通的近似立方图.此外，对于G-S的一个非平凡分支，令C*是通过添加新的顶点v并将其与C的三个2度点相连而得到的图.从而C*是3-连通的.否则，存在C*的一个2-点割T必定包含v,因此T中另一个点成为C的一个割点，矛盾.

通过归纳假设，G-S的每个非平凡分支C可以被分解成一些3-star与一些包含2-因子的2-连通近似立方图的并.另一方面，由于与S中的点相邻的边均被分解成中心在S的3-star.因此，G可以被分解成一些3-star和一些包含2-因子的2-连通近似立方图的并.

引理2顶点个数n≥6的4-正则图G,以下结论成立:

(i)κ′(G)∈{2,4}；

(ii)若κ′(G)=2,则G有一个不连通的2-因子.

证明：因为G是偶图，从而每一个边割均是偶的，也就是说κ′(G)∈{0,2,4}.同时，由G是连通图，即κ′(G)≥1.结论(i)成立.由定理1，G含有一个2-因子F.如果F不连通，则结论成立.因此假设F是一个Hamilton圈.由假设(ii)，设E′={e1,e2}是G的一个2-边割.显然有E′⊆E(F),否则与F的Hamilton性相矛盾.从而可知G⊆E(F)是一个不连通的2-因子.

2 主要结果

引理3任意二部立方图H,L(H) 包含一个不连通的2-因子.

证明设H是一个二部图，顶点集为(X,Y),G=L(H).显然,对于顶点x,G[E(x)] 是一个三角形，这里E(x)是指在H中与x相邻的边集.因此，{G[E(x)]:x∈X} 是一个每个分支都是一个三角形的不连通2-因子.

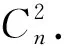
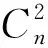
情形1当k≥2时,n=3k.

情形2当k≥2时,n=3k+1.

情形3当k≥2时,n=3k+2.

定理5若H是立方图，则G=L(H)包含一个不连通的2-因子.

证明容易看出，若H包含一个不连通的2-因子，则G也含有一个不连通的2-因子. 因此，假定H是2-因子Hamiltonian的.容易证明κ(G)=3.取顶点v∈V(H)使得κ′(H-v)=2.由推论3，H-v可以被分解成一些3-star与一些含有2-因子的近似立方图.从而可得L(H)包含一个不连通的2-因子.

定理6若G是顶点个数n≥6且包含K4的4-正则图，则G中存在一个不连通的2-因子.

证明由定理1，G包含一个2-因子C.如果C是不连通的，则结论成立.因此，假设C是连通的，即，C是G的一个Hamilton圈.

情形1n是偶数.

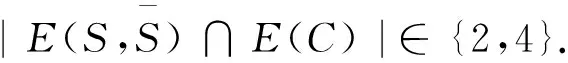
对每个i∈{1,2,3,4},令xi′∈V(G)〗{x1,x2,x3,x4}为xi在G中的邻点.若x2′=x3′,则x2,x2′,x3,x1,x4,x2是G〗E(C)中的一个5圈，也就是说,G〗E(C)是G的一个不连通2-因子.因此，假设x2'≠x3',令M是C中包含x2x3的一个完美匹配.我们考虑立方图G〗M.如果G〗M包含一个不连通的2-因子，结论成立.令M*是G〗E(C)中包含{x2x2′,x3x3′,x1x4}的一个完美匹配.从而G〗(M∪M*)是G中包含一个同构于C4的分支x1,x2,x4,x3,x1的完美匹配.

情形2n是奇数.

假设G中不存在两个点不交的4-团.否则，令S1,S2⊆V(G)满足S1∩S2=∅且对每个i∈{1,2}均有G[Si]≌K4.设G′=G/S1即G收缩S1.易得G'是包含一个K4且顶点个数是偶数的4-正则图.根据情形1，G'包含一个不连通的2-因子.取G'的一个顶点s,Cs是G中不连通分支C'中的一个圈.不妨设s1与s2是s在C′s上的两个邻点.不失一般性，对每个i,令si是xi∈S1的邻点.在Cs′中用s1x1x3x4x2s2替换s1ss2,可得G中的一个圈Cs.在C'中用Cs代替Cs′,即可得G中的一个不连通的2-因子.

因此，假设S⊆V(G)满足G[S]≌K4.注意到G/S是4-正则图.如果G/S是二部图，由定理4可得其中存在一个不连通的2-因子.从而G中亦包含一个不连通的2因子.因此我们假设G/S不是二部图，所以G0=GS也不是二部图.

情形2.1|N(S)S|=4.

情形2.2|N(S)〗S|=3.

S中的两个顶点在V(G)S有共同的邻点x,其余两个顶点在V(G)S中有两个邻点.若x的邻点为x2,x3,与情形1类似，GE(C)是G的一个不连通2-因子.否则，可以假设x1,x2的公共邻点是x,即x=xn.如果x3x6∈E(G),那么存在C的一个匹配M0不包含x5,x6和xn.因此，由推论1可得G0M0包含一个2-因子.否则，C的一个最大匹配M0在G0中不包含xn.考虑图G'0=G0M0,它是一个非二部图的近似立方图.根据推论2可得G'0包含一个2-因子，从而G包含一个不连通的2-因子.

情形2.3|N(S)〗S|=2.

S中的所有顶点在V(G)S有两个公共的邻点x5,xn.如果x2,x3在V(G)S公共邻点，则G〗E(C)即为G的一个不连通2-因子.因而我们假设x2xn与x3x5都在E(G)中.

令S1={x1,x2,x3,x4,x5,xn}.类似于情形2.1与情形2.2的讨论，如果|N(S1)|=4或是|N(S1)|=3,设G1=G〗S1,则C中存在一个不包含x6或xn-1的最大匹配M1.考虑图G'1=G1M1,它是一个非二部图的近似立方图，根据推论2，其中存在一个2-因子.从而G包含一个不连通2-因子，其中一个分支是x1,x3,x5,x4,x2,xn,x1；或者G〗E(C)即为G的一个不连通2-因子.

否则,|N(S1)|=2,也就是说x5,xn在V(G)〗S1中仅有两个邻点x6和xn-1.令S2=S1∪{x6,xn-1}.如果|N(S2)|=4或者|N(S2)|=3,我们可以得到一个不连通2-因子，其中一个分支是x1,x2,x3,x4,x1,另一个分支为x5,xn-1,xn,x6,x5；或者G〗E(C)即为G的一个不连通2-因子.

与以上讨论相同，对i≥1,若|N(Si)|=4或|N(Si)|=3,G中存在一个不连通的2-因子，其中一个分支是x1,x3,x5,x4,x2,xn,当i是奇数时；或是x1,x2,x3,x4,x1,当i是偶数时.反之，|N(Si)|=2,我们可以构造Si+1.由于n是一个奇数，每次添加两个点到Si,因而存在i*,使得|N(Si*)|≥3.此时，通过情形2.1与情形2.2的相同的证明我们即可以得到G的一个不连通2-因子.

推论4顶点个数至少是6的4-正则无爪图包含一个不连通的2-因子.