科氏力下带有内表面张力的黏弹性流体的瑞利—泰勒问题的稳定性
吴兴奇,刘蒙蒙,宋方应
(福州大学数学与统计学院, 福建 福州 350108)
0 引言
考虑重力场下的两层完全平行的互不混溶流体,其中较重的流体层在较轻的流体层上方,对这种平衡状态进行较小的扰动时,会导致较重的流体在重力作用下向下移动,而较轻的流体向上移动,并且这种不稳定会进一步增长,且伴随势能释放. 这种不稳定现象是由英国的两位物理学家Rayleigh[1]和Taylor[2]最早独立研究,故称之为RT不稳定性. 过去的几十年里,人们已从物理和数值方面对该现象进行广泛的研究[3],并且还进一步研究了其他物理因素,比如弹性[4-5]、旋转[3]、内表面张力[6-7]、磁场[8-10]等,如何影响RT不稳定性的演化. 最近,文献[4]研究了平板内无内表面张力的分层不可压缩黏弹性流体的瑞利—泰勒问题的稳定性. 本文在文献[4]结果基础上进一步考虑有内表面张力和旋转情形, 其数学模型如下:

(1)
这里,带有下标“+”“-” 的符号f+,f-分别表示有关上下层流体的未知函数或物理参数f.符号Ω+(t),Ω-(t)分别指上部流体区域和下部流体区域,由于考虑水平周期运动,故其分别定义如下:
Ω+(t)∶={(xh,x2)T∈R3|xh∶=(x1,x2)T∈T,d(xh,t) (2) Ω-(t)∶={(xh,x3)T∈R3|xh∶=(x1,x2)T∈T, -l (3) ρ∶=ρ+χΩ+(t)+ρ-χΩ-(t) (4) (5) 主要在数学上建立一个稳定性准则,在该稳定性准则下,上述VRT问题存在关于时间指数稳定的解,并且当κ适当大时,即可满足该稳定性准则. 此外稳定性准则与旋转角速度大小无关,见定理1及注1. 结果表明: 旋转不具有使流体失稳的效果. 由于直接证明VRT问题的稳定性结果是有困难的,为此,下面需要在拉格朗日坐标下重写VRT问题,并给出拉格朗日坐标下的稳定性结果和证明. 当然通过拉格朗日坐标逆变换即可得到对应的VRT问题(5)的稳定性结果. 定义固定的拉格朗日域Ω+∶=T×(0,τ),Ω-∶=T×(-l, 0),并定义流映射ζ±为以下初始值问题的解: (6) 在介绍变换(分层)VRT问题(6)稳定性数学结果之前,还要介绍一些简化的数学符号. 现在开始介绍VRT问题(6)的稳定性结果. (7) 上述H0和A0都通过η0来定义,分别表示H和A的初始值; 正常数δ依赖于区域Ω和其它已知的物理参数ρ,μ,g,θ和κ. 利用标准的迭代方法,很容易建立起变换VRT问题(6)存在关于时间的局部解,因此为了得到定理1的结论,只需建立起先验的稳定性估计式(7)即可. 为此假设(η,u,q)为变换的VRT问题的光滑解,并满足定理1中关于初始值的假设条件,以及下式成立: M(t)≤δ∈(0, 1) (8) 其中:δ充分小,依赖于区域Ω和其他已知的物理参数ρ,μ,g,θ和κ.则利用标准能量方法,可建立起如下能量不等式. (9) (10) 证明 上述证明可直接参考文献[10],故从略. 其中 则存在下列关于(η1,u1,q1)和(η2,u2,q2)的先验估计: (11) 其中: (12) (13) 此外 (14) 证明 可直接参考文献[10]得出,故从略. 首先从式(9)和式(11)得出,存在常数c和足够大的常数c1满足: (15) 注意K1和K2是正定泛函,则由式(10)的第一个估计和式(13),得出对充分小的δ,有: (16) 此外,可以参考文献[10]中的式(8.45)~(8.51)推出下式: (17) (18) 注意T1和T2是正定泛函,利用式(8)和式(10)的第二个论断,可以从式(15)和式(17)推出,对于充分大的常数c1和充分小的δ,满足: (19) 对上式关于t积分,并利用式(10)的第一个论断,即有: (20) 由式(12)的表达式,以及(η1,u1)和(η2,u2)所满足的初始条件,再利用上式估计,使用式(14)的第一个估计和迹定理,可知: (21) 对式(14)的第二个估计式关于β在Υ4, 4上积分,并利用迹定理,即得: (22) 最后将式(21)~(22)代入式(20)中,再利用式(18),即得先验稳定性估计式(7). 利用先验稳定性估计及局部解的存在性结果,即可得到定理1.





1 拉格朗日坐标下的运动方程组

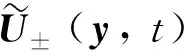


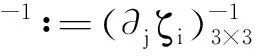

2 主要结果










3 定理1的证明


















