自动驾驶环境下交通均衡分配模型及算法

刘诗序, 贺朝阳, 朱建超, 王叔雨, 王皓宇

(1. 福州大学土木工程学院，福建 福州 350108; 2. 上海市隧道工程轨道交通设计研究院，上海 200235)

0 引言

随着城市的发展，越来越多的土地用于建设机动车的道路和停车设施，步行和非机动车出行吸引力下降，也变得更加危险，而自动驾驶汽车(autonomous vehicles，AVs)的出现将改变人们的出行方式. AVs不仅可以改善交通运行状况[1]，提高安全性和燃油效率，而且还可以减少驾驶人的工作量，为弱势群体的出行提供便利[2-4]. AVs通常还会改善汽车的排队行为，而且随着人工智能和工业技术的发展，在可预见的未来实现汽车自动化是可能的[5]. 自动驾驶汽车是通过消除驾驶中的人为错误来减少交通事故风险，而人们对其大规模使用的潜力及其对交通影响的了解却很少[6]. 因此，对自动驾驶汽车的交通研究非常有价值.

在交通均衡分配领域，学者们通常依据用户均衡(user equilibrium, UE)原理研究网络流量模式，UE原理最初由Wardrop提出，随后学者们在交通网络均衡建模方面进行了深入研究. UE原理假设每个出行者都将自己的出行成本降至最低，并且没有人能够通过单方面更改其路径来进一步降低个人成本[7]. 由于AVs可以获取交通状况的准确信息，因此可以基于UE原理分析自动驾驶环境中的网络均衡问题，学者们针对AVs和普通车辆混行的网络均衡问题做了一些研究[8, 9].

但是，对于AVs均衡问题的研究普遍没有考虑停车需求，由于停车活动是出行过程中必不可少的环节，它会对交通网络均衡产生影响. 普通汽车网络均衡考虑停车需求的研究较多[10-11]，而AVs在这方面的研究很少. 考虑停车选择的AVs交通模式与普通车有很大不同，具有3个新特点： 对出行者而言，不需要花费时间去寻找停车场，AVs自动驾驶寻找停车场； AVs不需要在目的地附近停车，可选择远离目的地和市中心的区域停车； AVs可以就近(相对于目的地)将出行者放下，然后自主寻找停车场，这样出行者节省了从停车场到目的地的步行时间[12]. Liu[13]首次建立AVs的出发时间和停车选择的联合均衡模型，Zhang等[14]在此基础上还研究了早晚通勤模式. 他们研究的是共享AVs出行[13-14]，在可预见的未来，AVs应该存在两种运营方式： 私有和共享[15]，考虑到便捷性、可靠性、成本等因素，很多学者认为消费者更倾向于拥有私人AVs[16-18]. Levin[19]在私人AVs和公交车、普通车辆混行中不仅考虑了停车选择，还考虑了交通方式选择，但他的研究假设AVs只能回家停车，在实际中，当家庭停车场太远时，AVs可以选择公共停车场. Zhang等[12]在私人AVs环境中考虑了停车费对网络均衡结果的影响，但他认为出行者在起点就先进行停车场选择，这可能出现即使总出行成本最低，但载人阶段出行成本相较于其他方案不是最小的现象，这对于追求出行时间最短的用户来说是不合理的.

城市交通拥堵主要发生在通勤时段，特别是在早高峰期，大多数出行者需要按时抵达目的地. 因此，本文针对这种情况，将整个出行过程划分为两个阶段： 从起点到目的地，和从目的地到停车场，研究两个阶段同时均衡的问题. 基于此，本文考虑AVs行驶过程中空载和载人状态的差异，首先针对路段成本函数的Jacobian矩阵对称情形建立相应的数学规划模型，而后推广至更一般的Jacobian矩阵不对称情况，并给出算法的解满足均衡条件的证明.

1 自动驾驶环境下交通均衡分析

1.1 路径选择过程

普通车辆与AVs的交通模式是不同的，主要体现在停车选择上. 普通车辆的出行过程可以概括为： 从起始节点出发→选择停车场停车→步行至目的地，如图1. AVs的出行过程可概括为： 从起始节点出发→抵达目的地放下出行者→空载寻找停车场停车，如图2.

图1 普通车辆路径选择过程Fig.1 Regular vehicle routing process

图2 AVs路径选择过程Fig.2 AVs routing process

因此，AVs的出行过程分为两个阶段： 第一阶段是载人阶段，从起始节点出发将出行者送至目的地； 第二阶段是空载阶段，从目的地出发空载行驶寻找停车场停车. 需要注意的是，本文将两个选择过程分开分析，目的是突出AVs与普通汽车之间的不同，其整个决策过程仍是同时完成的，即出行者事先规划好出行路径以及选择好停车场，因此，本文研究的是AVs的静态均衡问题，所建立的模型不体现决策的先后顺序. 另外，本文讨论的停车场包括家庭停车场和公共停车场两类.

1.2 交通网络及成本函数

假设网络G=(N,A1)，其中N为所有节点集合，A1为所有实际路段集合.令P为停车场集合(p∈P)，包含两类停车场，家庭私人停车场和公共停车场； 令R为所有出发地的集合(r∈R)；S表示所有目的地的集合(s∈S).Krs表示OD(起点O到终点D的距离)对r-s间的所有路径的集合，Lsp表示OD对s-p间的所有路径的集合.需要说明的是，在实际问题中起始节点集合、目的地集合和停车场集合可能存在交集，即同一节点既可能是起始节点，还可能是目的地或停车场.

令载人AVs出行需求量为qrs，空载AVs出行需求量为qsp, r，有如下关系

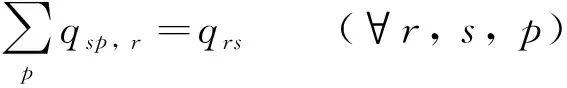
(1)

(2)

(3)

(4)

载人AVs和空载AVs虽然是同种车型，但在道路上运行状态存在差异. 因为出行者希望尽可能地减少自己的出行时间，所以行驶速度较快. 而AVs空载寻找停车场过程中，出行者并不在车内，他们更关注AVs的能源消耗. 一般地，出行时间的增加意味着出行距离的增加或车速的降低，这可能导致能源消耗成本增加[12].

假定路段a∈A1上的路段行驶时间(行驶成本)函数是单调递增函数

ti, a=ti, a(x1, a,x2, a)

(5)

式中：ti, a表示路段a上的路段行驶时间函数，i=1时表示载人AVs，i=2时表示空载AVs.

由于AVs出行的第二阶段主要以能源消耗为路径选择依据，假设能源消耗是路段行驶时间的单调递增函数，能源消耗g2, a(x1, a,x2, a)可以表示为

g2, a(x1, a,x2, a)=G(t2, a(x1, a,x2, a))

(6)

将路段行驶的能源消耗转换为路段行驶时间

h2, a(x1, a,x2, a)=α·g2, a(x1, a,x2, a)

(7)

式中：h2, a(x1, a,x2, a)表示路段a上的空载AVs的能源消耗转化成的行驶时间；α为能源消耗与时间之间的转换系数.

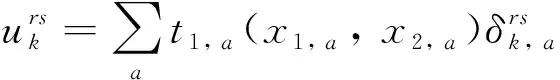
(8)

(9)

对于空载AVs，出行成本不仅要考虑能源消耗，还要考虑停车费用. 本文将停车场分为家庭停车场和公共停车场，区别是家庭停车场仅供个人使用不对外开放，而公共停车供所有车辆使用. 对于拥有家庭停车场的出行者，在自己的家庭停车场停车的费用为0，而对于其他节点出发的出行者不允许在此处停车，停车费用可视为无穷大. 公共停车场的停车费用假定为定值. 停车成本可表示为

Cr, p=β·cr, p

(10)

式中：Cr, p表示从起始节点r出发选择停车场p的停车成本；cr, p表示从起始节点r出发选择停车场p的停车费用；β是费用与时间之间的转换系数.需要说明，式(9)的出行成本与AVs从哪里出发无关，而式(10)与起始节点有关，为了后续的统一表达以及建模方便，式(9)也考虑了起始节点.

1.3 均衡分析

由于AVs可以获取完全的路网信息，假设其路径选择服从Wardrop用户最优原则，因此路网可以达到确定性的用户均衡状态.

载人AVs总是选择从起点到目的地的最短路径使得出行成本最低，均衡条件可以表示为

(11)

式中：μrs表示网络达到均衡状态时OD对r-s间的最小出行成本.

空载AVs总是选择从目的地到停车场的最短路径使得出行成本与停车成本之和最小，均衡条件可以表示为

(12)

式中：μsp, r表示网络达到均衡状态时OD对s-p间的最小出行成本；λs, r表示网络达到均衡状态时OD对s-p间的最小净出行成本，包括路径出行成本和停车成本两部分.

2 对称型均衡模型

2.1 模型

首先假设路段成本函数的Jacobian矩阵是对称的，即

(13)

在OD需求量固定的前提下，参考已有普通车辆路段行驶成本相互影响的网络均衡建模方法[7, 20]，建立AVs的路径和停车选择的联合均衡数学规划模型

(15)

式中：w和v为积分变量，分别对应载人AVs和空载AVs流量.

建立拉格朗日函数，容易证明模型与均衡条件(11)～(12)等价，证明过程可参考文献[7].

2.2网络变换

上述模型是考虑路段流量相互影响，并且包含停车场选择的组合均衡模型. 为了求解方便，可以在网络中添加虚拟讫节点r′，任何从起始节点流出的流量都会流入相应的虚拟讫节点.

图3 一般等价网络Fig.3 Equivalent network

令A2表示虚拟路段的集合，A=A1∪A2，对于空载AVs的路段出行成本可以改写为

(16)

因此数学规划模型(14)～(15)可以改写为

(18)

(19)

(20)

观察变换前后的目标函数，两者本质上是相同的. 变换路网后的均衡问题是标准的UE问题，所以模型存在唯一解，即路段流量和停车场需求量是唯一的. 标准UE的求解方法比较成熟，此处不再赘述. 下一节讨论另一种情况： 路段成本函数的Jacobian矩阵不对称.

3 非对称型均衡配流

3.1 算法

实际中，上述问题的Jacobian矩阵常常是非对称的，找不到一个等价的极小值问题，使得它就是该问题的均衡解[21]. 本节直接提出适用于本文交通均衡问题的对角化迭代算法，这种算法类似于求解标准UE问题的方向搜索算法，它是基于一系列的标准UE子问题，即每次迭代都要计算下列子问题：

第一步: 初始化.令n=0，设置网络属性、出行成本函数等基本参数，设置初始可行流x(n).

第二步: 求解“对角”问题.使用MSA算法求解上述标准的UE子问题，设产生的流量为x(n+1).

第三步: 收敛性检查.若x(n)≈x(n+1)，停止； 否则置n=n+1，转入第二步.

收敛检查，可以使用下式判断

其中，MSA算法具体步骤可参考Mounce[22]的论文，收敛检验方法如下

需要注意的是，要使上述问题有唯一解，路段成本函数的Jacobian矩阵必须正定[7]，正定的条件是： 1) 两种行驶状态下的路段行驶成本函数是其流量的增函数； 2) 两种行驶状态下的路段行驶成本主要受自身流量的影响. 一般的交通网络中这两个条件是成立的，从而可以推出上述问题有唯一解.

3.2 解的特性

3.2.1充分性——若x(n)=x(n+1)，则x(n)是用户均衡解

考虑上述对角子问题的一阶条件，即

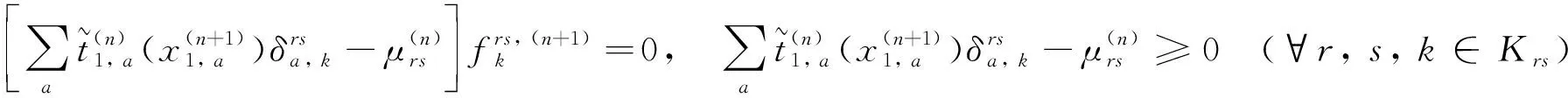
(21)

(22)

(23)

当收敛条件成立时，即

(24)

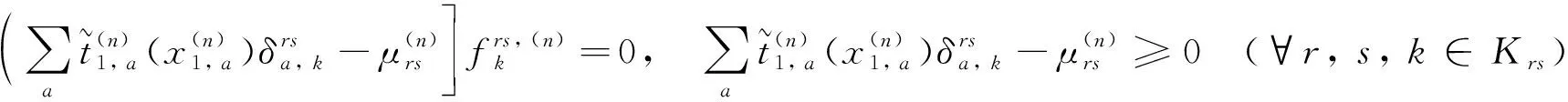
(25)

(26)

此时有

(27)

(28)

则(25)～(26)变为

(29)

(30)

式(29)～(30)表明x(n)是一个平衡解，证毕.

3.2.2必要性——若x(n)是用户均衡解，则x(n)=x(n+1)

若x(n)是用户均衡解，根据用户均衡原则，x(n)满足(29)～(30)，即满足均衡条件所对应的UE子问题. 通过第二步迭代计算，该UE子问题可以得到一个均衡解x(n+1).而由于Jacobian阵是正定的，UE子问题有唯一解，所以x(n)=x(n+1).

4 算例

图4 交通网络结构Fig.4 Transportation network

本算例网络结构如图4，共有两个OD对，如图中实心圆，分别为OD和O′D′，需求量分别为qOD=1 000 pcu·h-1和qO′D′=1 500 pcu·h-1, pcu(passenger car unit)表示标准车当量数. 共有四个停车场，其中停车场1(P1)和停车场3(P3)为家庭停车场，停车场2(P2)和停车场4(P4)为公共停车场.

路段行驶时间函数采用下列形式

表1 路段属性

表2 停车费

图5 收敛指标变化Fig.5 Convergence change

基于上述条件，令外部收敛因子ε1=0.1，内部收敛因子ε2=0.000 1. 当η1=0.6、η2=0.9时，图5显示了对角化算法外部迭代收敛情况. 在外部迭代计算13次后，算法达到收敛标准，说明算法是有效的.

起点O产生的需求包括载人和空载AVs两种，对于载人AVs前往终点D共有6条有效路径，在均衡状态，有3条路径被选择，分别为2-5-8-11(路段编号)、2-5-9-12和2-6-10-12，出行成本为26.2 min； 对于空载AVs前往各停车场共有15条有效路径，在均衡状态，全部选择停车场3，出行成本为28.7 min. 起点O′产生的需求中，载人AVs前往终点D′共有6条有效路径，在均衡状态，共有3条路径被选择，分别为14-17-20-23、14-17-21-24和14-18-22-24，出行成本为25.2 min； 对于空载AVs前往各停车场共有10条有效路径，在均衡状态，选择了停车场1和4，出行成本为26.5 min.

图6显示了当η1=0.6、η2=0.9和η1=0.7、η2=0.7时，随着停车场2的费用减少，周围8个路段的流量变化情况，虚线表示远离停车场2的路段流量，实线表示流向停车场2的路段流量. 在分别测试了多个折减系数对路段流量的影响后，图6所示路段流量变化趋势基本相同，仅折线的拐点和变动幅度有区别，造成这种现象的原因也是相同的.

(a) η1=0.6、η2=0.9

(b) η1=0.7、η2=0.7

本文以图6(a)为例进行说明，图6(a)列出了两组有代表性的非对称情况路段流量变化的实验结果，停车场2的费用刚开始减少时对周围路段没有影响(0%～31%)，紧接着周围路段流量发生剧烈变化(31%～52%)，然后个别路段趋于稳定，随后个别路段流量出现微小的变化(52%～73%)，最后停车场2的费用继续减少对路段流量不再产生影响.

图7显示非对称情况下，随着停车场费用的减少，4个停车场需求量的变化情况. 可以发现停车场2的费用刚开始减少对各停车场需求量没有影响(0%～31%)，随着费用的持续下降，选择停车场2的流量逐渐增多，其他停车场的需求量会减少(31%～52%)，停车费继续下降对各停车场需求量不再产生影响.

如果把本算例的网络看成一个城市的交通网络，那么停车场2相当于市中心的公共停车场. 产生上述流量变化可以归结为停车场费用和路段行驶时间两方面原因，停车场费用的减少势必会吸引大量的空载AVs涌入，同时会增加停车场附近路段的负荷，增加路段行驶时间. 所以当停车场费用为主导因素时，随着停车场2的费用减少，流向停车场2的路段流量普遍上升，而远离停车场2的路段流量普遍下降，如图6所示，同时停车场2的需求量急剧增加，其他3个停车场的需求量全部减小，如图7所示. 当停车场费用影响不起作用时，路径流量和停车场需求量不再变化.

图8显示了个人出行总成本的变化情况. 可以发现随着停车场费用减少，总出行成本有相同的变化趋势. 刚开始对总出行成本没有影响(0%～31%)，紧接着总出行成本波动变化(31%～52%)，随后出行成本与停车费用呈现线性变化关系. 产生波动变化的原因和上述停车需求变化原因相同.

图7 停车需求量变化情况(η1=0.6、η2=0.9)Fig.7 Change of parking demand(η1=0.6、η2=0.9)

图8个人总出行成本变化情况(η1=0.6、η2=0.9)Fig.8 Change of individual total travel cost(η1=0.6、η2=0.9)

5 结语

本文在全自动驾驶环境下，假设载人和空载AVs将达到各自的均衡状态，基于此建立了路径选择与停车选择的联合交通均衡模型及算法，并证明了算法解满足载人和空载AVs的用户均衡原则. 算例分析表明，载人和空载AVs的均衡状态的确存在差异，且差异的大小与两者之间的相互影响程度有关. 此外，随着停车费的降低，中心停车场的需求量以及流向中心停车场的路段流量急剧增加，个人出行成本呈现总体下降趋势. 这意味着人们在享受AVs带来便利的同时，还需面临AVs停车过程造成局部路段拥堵带来的挑战.

短期内仍难以实现AVs的全覆盖，所以同时考虑普通车辆混行也有很大现实意义，后续可以研究普通车辆和自动驾驶车辆多方式网络均衡问题. 另外，AVs可以实时获取路网数据，所以后续还可以研究自动驾驶环境下的动态交通分配问题.