基于学业质量水平划分的数学建模教学设计
陈旭 汤小青



摘 要:结合数学建模过程和数学建模素养的三个水平对“茶水的最佳饮用问题”进行三个维度的教学设计:了解过程,体会模型;经历过程,建立模型;感悟原理,创新模型. 从进阶型设计、不同模型类型设计、素养型设计、学生型设计四个角度进行教學设计的反思,以期更好地落实数学学科核心素养的培养.
关键词:数学建模;水平划分;设计反思
一、数学建模素养及其三个水平划分
《普通高中数学课程标准(2017年版2020年修订)》(以下简称《标准》)中指出,数学建模素养是对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题的素养. 数学建模过程主要包括在实际情境中从数学的视角发现问题、提出问题、分析问题、建立模型、确定参数、计算求解,检验结果、改进模型,最终解决实际问题.《标准》从情境与问题、知识与技能、思维与表达、交流与反思四个方面给出了数学建模素养的三个水平划分. 从以上分析可以看出,可以从实际情境抽象、经历完整过程、构建数学模型、检验改进模型等关键问题上将数学建模素养的三个水平划分和数学建模过程有机结合进行单元教学设计,从而更好地发展学生“四能”,达到“三会”,落实数学建模素养的培养.
二、“茶水的最佳饮用问题”教学设计
1. 创设情境,提出问题
中国茶文化博大精深,自古以来中国人有饮茶的传统. 唐代诗人白居易的《山泉煎茶有怀》:“坐酌泠泠水,看煎瑟瑟尘. 无由持一碗,寄与爱茶人.”这首诗就描述了古人饮茶的传统.
怎样才能喝到一杯好茶?学生经过社会调查和资料搜集分析,发现以下几个因素会影响茶水的口感:茶叶的类型、水质、茶具的品质、泡茶的技艺、水沸腾的时间、泡茶的水温、喝茶的水温等. 从上述调查可以发现,在客观条件有限的情况下,茶艺的精进和水温的控制是成就一杯好茶的重要因素. 本次数学建模活动就从水温的控制入手,力求喝到一杯好茶.
调查表明:某种绿茶,泡茶的水只需要煮沸即可,不易煮沸太久;泡茶的最佳水温为[85℃];饮茶的最佳温度为[60℃]. 那么在[24.3℃]的室温下,如何才能利用数学的方法预测最佳水温,泡出一杯好茶,饮得一杯好茶呢?
【设计意图】以传统文化为背景,从生活入手,让学生经历社会调查、资料搜集的过程,积累社会活动经验,发现、提出数学问题.
2. 维度1:了解过程,体会模型
为了泡出好茶,先要烧出适合泡茶的好水. 水煮沸的时间过长容易影响水中矿物质的构成,影响茶水的口感. 那么,如何预测水升温至[100℃]所需要的时间呢?
(1)模型的假设.
问题1:影响水升温至[100℃]所需要的时间的因素是什么?建立模型需要哪些假设?
热源的热量释放速率和稳定性是水温上升的能量保障;煮水器物的热传导性影响热量的传导速率;大气压的大小影响水的沸点;溶解于水中的矿物质也会影响水的沸点. 综上所述,影响水升温至[100℃]所需要的时间的因素大致有热源、烧水器具的材质、气压、水源等. 假设在相同的热源、相同的烧水器具、标准大气压、相同的水源等条件下,抽象出以时间为自变量、以温度为因变量的函数关系.
【设计意图】从物理学角度分析具体现象中的各种变量,感受现实问题的复杂性,通过模型假设为现实问题数学化及数学模型的建立做必要的准备.
(2)模型的建立.
① 学生活动:小组合作采集数据.
实验器材:温度采集器、家用普通电热水壶、矿泉水.
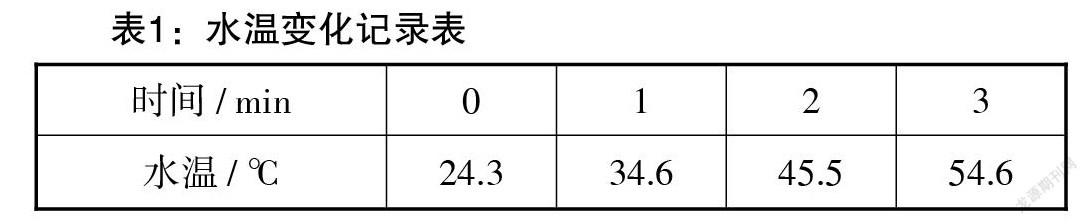
实验条件:室温[24.3℃]、标准大气压. 每隔1分钟记录一次数据,记录数据如表1所示.
[时间 / min 0 1 2 3 水温 / ℃ 24.3 34.6 45.5 54.6 ][表1:水温变化记录表]
【设计意图】数学的抽象需要以具体的情境和数据为依托,需要学生用数学的眼光设计和分析实验,通过实验发现和总结规律,最终将现实问题抽象成数学问题.
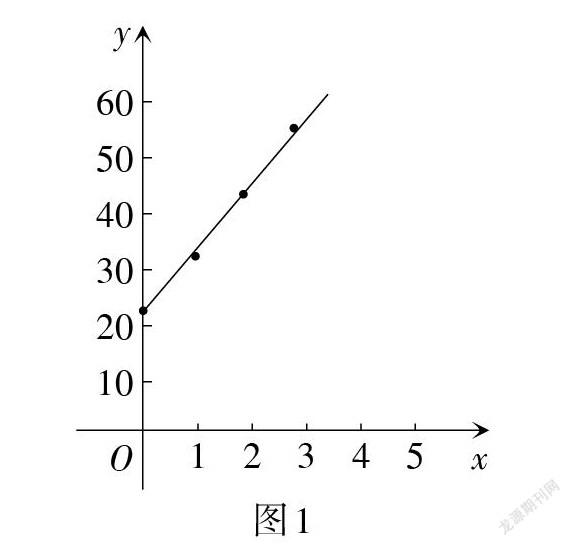
② 利用Excel软件作散点图,并进行回归拟合,时间与水温的函数关系如图1所示,拟合函数为[y=][10.18x+24.48],其中[R2=0.998 8](拟合优度,也称为决定系数,越靠近1,拟合效果越好).
【设计意图】将数据以直观的散点图进行呈现,将抽象的数据信息直观化,更好地揭示数学问题的本质. 借助Excel软件利用统计原理完成拟合过程,得到学生熟悉的一次函数模型,使学生在熟悉的模型中体会模型的数学意义.
(3)模型的检验和求解.
[R2=0.998 8],拟合度良好,测量数据近似符合线性关系,其中拟合函数[y=10.18x+24.48]中[x]的系数[10.18]为每分钟水温上升的速度,[24.48]为初始时刻对应的温度,经计算大约需要7.4分钟能将水烧开.
【设计意图】理解一次函数模型中参数的意义,并能利用模型解决问题,体会其中蕴含的数学思想,感悟数学表达对数学建模的重要性.
3. 维度2:经历过程,建立模型
在[24.3℃]的室温下,刚泡好的茶水(85℃)需要多长时间才能达到最佳口感(60℃)?
(1)模型的假设.
问题2:茶水的冷却时间与哪些因素有关?建立模型需要哪些假设?
物体温度降低放出热量,热量的释放与材料的热传导系数及空气分子的运动速度等有密切的关系. 故影响茶水冷却时间的因素有茶具的材质、室温、茶水与空气的接触面积、空气的流通速度等. 假设在茶具、室温、风速、空气接触面积等都相同的条件下,抽象出以时间为自变量、温度为因变量的函数关系.
【设计意图】利用相关知识对模型的影响因素进行分析,使学生能够在熟悉的情境中发现问题并转化为数学问题,知道数学问题的价值与作用.
(2)模型的建立.
① 学生活动:小组合作采集数据.
实验器材:温度采集器、85℃的茶水、标准[200 mL]烧杯.
实验条件:室温24.3℃、无风、含[200 mL]温度为85℃茶水的烧杯. 每间隔1分鐘记录一次温度,记录数据如表2所示.
[时间 / min 0 1 2 3 4 5 茶温 / ℃ 85.0 79.2 74.8 71.3 68.3 65.9 ][表2:茶水温度变化记录表]
② 作出散点图、添加趋势线,形成时间与茶温的函数关系,如图2所示.
问题3:结合所学的函数知识和图2,能否分析函数的性质?
设函数[y=fx],其中[x]为时间,[y]为[x]时刻的水温. 那么,函数[y=fx]的定义域为[x∈0,+∞],值域为[y∈24.3,85](单位:[°C]);函数[y=fx]在定义域上单调递减,递减速度越来越慢;对于函数[y=fx],当[x→+∞]时,[y→24.3].
【设计意图】从函数的定义域、值域、单调性、凹凸性和渐近线的角度分析趋势线的函数性质. 让学生利用数学概念和原理分析实验结果,用数学语言描述相应的数学规律.
③ 模型的选择.
问题4:能从三角函数、一次函数[y=kx+b]、二次函数[y=ax2+bx+c],以及形如[y=klogax+b]和[y=kax+b]的函数中选择一个你认为更合理的函数模型吗?
三角函数具有周期性,不符合函数存在渐近线的要求;一次函数不符合函数具有凹凸性的要求;二次函数不符合函数图象具有渐近线的要求. 函数[y=][klogax+b]不符合值域为[y∈24.3,85]的要求. 故最终选择函数[y=kax+b]作为函数模型.
【设计意图】引导学生利用函数的性质分析并选择合适的数学模型,表达所要解决的数学问题.
(3)模型的求解.
问题5:能否利用图象上的信息求解[y=kax+b]中的参数?
根据定义域,得[y=kax+b x≥0]. 因为值域[y∈][24.3,85],所以[b=24.3];利用单调性,知[0<a<1];利用特殊点[0,85],解得[k=60.7]. 由此可以得到[y=60.7ax+24.3 0<a<1,x≥0]. 其中,[60.7]就是起始茶温与室温的温度差. 具体情况如表3所示.
[[x] 0 1 2 3 4 5 [y] 85.0 79.2 74.8 71.3 68.3 65.9 [y-24.3] 60.7 54.9 50.5 47.0 44.0 41.6 [a] — 0.904 4 0.919 8 0.930 7 0.936 2 0.945 4 ][表3:比值求解参数[a]]
构造误差函数[fa=a-a12+a-a22+a-a32+][a-a42+a-a52]. 当[a=15a1+a2+a3+a4+a5]时,误差[fa]最小,故用[a]的平均值[a]估计[a]较为合理. 其中,[a=150.904 4+0.919 8+0.930 7+0.936 2+0.945 4=0.927 3.]综合以上分析,可得[y=60.7×0.927 3x+24.3 x≥0].
【设计意图】理解模型中参数的意义,知道如何确定参数,建立模型,求解模型. 从数学原理的角度推理、辨析算法,体验参数的计算过程,使学生的思维从浅层走向深入,体验数学思维分析问题的过程.
(4)模型的检验.
本次实验拟合函数[y=60.7×0.927 3x+24.3 x≥0],[R2=0.986],拟合效果较好. 由[60.7×0.927 3x+24.3=60],解得[x=log0.927 335.760.7≈7.040 9]. 故在室温[24.3°C]下,刚泡好的茶水([85°C])需要7分钟左右达到最佳口感([60°C]).
4. 维度3:感悟原理,创新模型
(1)模型再分析.
问题6:利用Excel软件进行多项式拟合,得到拟合函数为[y=116.16x+4-0.466+24.3],[R2=0.999 7],该函数是否更符合实际情况?
热力学基本原理:热量从高温物体向低温物体传导;在一定的温度范围内,一个物体的温度变化速度与这一物体的温度和所在介质温度的差值成比例(牛顿冷却定律).
证明:设物体在[t]时刻的温度为[y=ft],介质温度为[C0],物体初始温度为[T0]. 则温度的变化速度可以用[dydt]来表示,温度差表示为[y-C0][y>C0]. 由牛顿冷却定律,得[dydt=-ky-C0 k>0],这里[k>0]是比例系数. 整理,得[dy-C0y-C0=-kdt]. 两边积分,得[lny-C0=][-kt+C]([C]为任意常数),[y=ft=e-kt+C+C0=eCe-kt+C0]. 因为[f0=T0],所以[eC=T0-C0]. 令[a=e-k],则[0<a<1],那么[y=ft=C0+T0-C0at 0<a<1.]
通过上述分析和论证可以知道,虽然函数[y=][116.16x+4-0.466+24.3]具有较高的拟合度,但是并不符合实际的物体冷却规律.
【设计意图】将热力学基本原理与数学推理相结合,用数学语言清晰、准确地表达过程和结果,对模型的选择做出进一步论证.
(2)模型再改进.
在实际中,牛顿冷却模型中的参数[a=e-k]是在一定范围内成立的. 如何设计出更符合实际的模型,可以采取分段模型的策略来处理.
结合表3,可知前两分钟,[a1=120.904 4+0.919 8=][0.912 1;] 后三分钟,[a2=130.930 7+0.936 2+0.945 4≈][0.937 4]. 因此[y=ft=24.3+60.7×0.912 1t,0≤t<3,24.3+47×0.937 4t-3,3≤t≤5.]故[24.3+47×0.937 4t-3=60],解得[t≈7.254.]
【设计意图】基于原理的分析,有效解读参数的意义,创造性地解决生活中的实际问题.
三、三个水平划分的数学建模教学设计反思
1. 基于三个水平划分的进阶型单元教学设计
将数学建模的过程和数学学业质量三个水平的划分相结合,逐层进阶,从浅层走向深度,从形式迈向本质.
结合数学建模水平一的要求. 在维度1中,学生经历了模型假设、数据收集、利用Excel软件建立模型、模型检验、模型计算,了解了数学建模的过程,在熟悉的情境中,体会了用熟悉的一次函数模型解决问题的数学思想.
结合数学建模水平二的要求,在维度2中凸显了应用函数性质选择模型、计算参数的原理分析等过程,使学生经历了更为完整的数学建模过程,理解数学建模的意义,引导学生运用数学语言表达数学建模过程中的问题及解决问题的过程和结果,体现数学建模的“过程”“活动”特性.
结合数学建模水平三的要求,在维度3中进一步结合相关学科知识,用清晰、准确的数学语言推理了牛顿冷却模型,并在此基础上对模型进行改进和创新,创造性地建立数学模型,解决实际问题.
2. 基于不同类型建模活动的教学设计
文献[3]指出,高中数学建模活动分为两类:类型一是基于现实情境,建立模型、判断模型、求解参数,最终得出数学模型,解决实际问题;类型二是基于数量关系或空间形式有关的一般规律的发现,用数学语言描述形成一般模型.
基于类型一进行维度1和维度2的设计. 在这两个维度中基于现实情境,抽象出时间和温度的函数关系,通过数据和图形判断数学模型,求解参数,最终得出数学模型,解决实际问题. 基于数学建模的类型二进行维度3的设计,基于维度1、维度2的研究和相关学科知识建立温度和时间的一般规律,通过准确的数学语言表述规律、严谨的数学推理拓展规律,形成更一般化的模型,提升模型的普适性.
3. 基于素养培养的数学建模活动设计
“水温与时间”“茶温与时间”的抽象不是针对数学概念及概念之间的关系,而是用数学的概念、原理和思想方法从事物的具体背景中抽象出一般规律,并用数学语言表达为数学问题,是一个用数学眼光观察世界,从而发现和提出问题的过程,是落实数学抽象素养培养的良好着力点.
影响物体温度的影响因素复杂多变,而任何数学模型都有其使用范围,这个范围需要通过模型的假设、初始条件的设定、模型中参数的某些限制等方式给出. 显然,这个过程体现出与数据分析、直观想象、逻辑推理等素养的直接关联.
利用数据确定假设模型中的参数,通过计算求解得出数学模型. 这个过程也体现出与数据分析、数学运算、逻辑推理等素养的直接关联.
数学建模教学活动是一个综合的过程,在设计的过程中需要关注各种素养的综合渗透.
4. 基于学生主体性的数学建模活动设计
以小组合作学习的方式开展社会调查、资料收集、数据搜集等活动;以学生活动为中心,教师作为指导者和共同参与者促进学生学习;教师和学生共同构造良好的组织框架,创建学习环境,让学生在环境中建构知识和技能,围绕主题开展直接、深入的探究;重视学生的学习主动性,鼓励协作学习与合作学习,鼓励学生发挥自己的智力优势和学习长处;允许学生犯错和改正,营造开放的活动氛围,发展学生的高级思维技能;学生活动不是盲目地忙碌、活跃,而应该是有目的的行动.
参考文献:
[1]中华人民共和國教育部制定. 普通高中数学课程标准(2017年版2020年修订)[M]. 北京:人民教育出版社,2020.
[2]教育部基础教育课程教材专家工作委员会.《普通高中数学课程标准(2017年版)》解读[M]. 北京:高等教育出版社,2018.
[3]章建跃. 核心素养立意的高中数学课程教材教法研究[M]. 上海:华东师范大学出版社,2021.

