数学教学中“二次探究”情境的创设*
叶 忠
(福建省石狮市教师进修学校,362700)
数学探究活动是指围绕某个具体的数学问题,开展自主探究、合作研究并最终解决问题的过程.《普通高中数学课程标准》课程内容“主题五”指出:数学探究活动以课题研究的形式开展[1].课堂探究的目的是在课堂有限的时间内获得知识结论,探究问题要围绕教学知识目标,探究情境要更贴近学生实际,这就要求教师对课堂探究的情境进行精心预设.
创设情境让学生进行探究性学习是课堂教学中常用的教学手段,但知识的获得过程是复杂的,很多知识往往不能通过一次探究得到,需要二次探究甚至多次探究.本文对此进行探讨.
一、 课堂教学需要“二次探究”
所谓的“二次探究”,是指教学中针对某一研究内容,因为第一次探究没法达到教学目标而设计的再次探究.
数学探究并不是简单的思考,它以情境为载体,问题为核心,探究方法为手段,在所设置的问题情境指引下,经过猜想、验证,获得结论.课堂探究与普通的“思考”不同,犹如爬楼梯,“探究”指的是设计情境,指引如何“更上一层楼”,而“思考”指的是在问题引导下从第一个“阶梯”到下一个“阶梯”,在情境与目标距离上“探究”的开放程度更高.
“二次探究”的开展,可先猜想后验证,也可对同一问题从不同层次开展研究,还可以获得结论后再从不同角度研究问题.这样对问题开展多维度、多角度研究,真正深入问题的核心.因此,二次探究的开展可以让探究的空间更广阔,情境创设更多样化,真正促进学生课堂参与,促进思维品质提升和数学素养提升.
在一次探究基础上进行的“二次探究”让课堂探究手段更丰富.借助情境开展探究,可以创设纯问题情境、实物情境、操作实验情境、多媒体演示情境等进行“二次探究”.“二次探究”所创设的情境更加深入问题本质,情境大多以学科素养水平二为主,少数达到水平三.
二、 创设“二次探究”情境,深化课堂教学
对于一些数学核心问题,特别是命题教学,“二次探究”能让课堂教学更流畅,更利于学生发现问题、研究问题.
1.渐进式深入研究,提高问题解决能力
案例1平面与平面平行的性质
探究1类似直线与平面平行的判定,已知两个平行平面,可以得到什么结论?
探究2如图1,已知平面α∥平面β,我们知道,线动成面,若直线a∥平面α,当直线a变化时,你可以得到什么结论? 如果直线a与平面α相交呢?

探究1是渗透类比的问题研究方法,让平面与平面平行性质的研究方法与直线和平面平行判定的研究方法进行类比,让学生想到平面与平面平行问题可以转化为直线与平面问题,进而转化为直线与直线问题.这一探究只给出探究对象(两个平面),方法不具体,目标不明确,开放水平较高,探究渗透了降维和转化的思想,但大部分学生不能实现探究的目的,获得所需要的结果.
探究2的完成需要以下几个环节:环节一:直观想象,直线——平面——直线,即直观想象变化直线成平面,研究平面与平面的交线;环节二:从各种直线动态变化中,抽取共性结论;环节三:猜想——验证,猜想出定理内容,尝试推理论证.探究2探究内容明确,方法清晰,不约束学生思维,结论开放,知识的获得过程自然,操作性强,能调动学生探究热情.学生可以从直线a与平面α相交和平行两种情况出发,通过直观想象,当直线a运动时,能得到一些平面与平面平行的相关结论,经过学生间的交流,在直线a与平面α相交和平行两种情形下,平面与平面平行的性质定理对应的结论还是比较容易获得的.
教师只需适当地提示,多数同学就可以抽象出定理,部分没有得到定理或认识不深刻的同学,通过后续的动画演示,可以深刻理解定理的内容.
2.知识横向联系探究,培育学科素养
案例2基本不等式
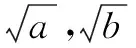
探究2AB是圆的直径,点C是AB上一点,AC=a,BC=b.过点C作垂直于AB的弦DE,连结AD,BD,你能利用这个图形,得出基本不等式的几何解释吗[2]?
探究1是在前面不等式的基础上,对问题进行深入研究,即利用a,b的一般性,通过给出研究方法,获得基本不等式.这一探究建立在原有知识基础上,通过知识间的联系获得的公式,学生对公式的获得过程印象深刻.
探究2是基本不等式的几何解释,“二次探究”的完成需要以下几个环节:环节一:数形结合,挖掘题目中的条件,探索可能出现的结果;环节二:在诸多结论中,找到体现基本不等式几何意义的关系式或相近关系式;环节三:结论与模型进行联系,体会为什么可以实现这一联系,基本不等式在几何图形中是如何体现的.探究2更多的是利用初中的平面几何知识进行探究,虽然探究给出了方法提示和探究结论,由于知识的遗忘,探究的过程对多数学生还是有一定困难的.但这一探究却是很好的教学素材,一方面让学生体会基本不等式的代数与几何之间的统一性,另一方面通过几何解释可以训练学生思维的深刻性和灵活性,培养直观想象和逻辑推理等素养.
3.先猜想后验证,渗透研究方法
案例3正弦定理
探究1余弦定理及其推论分别给出两边及其夹角、已知三边直接解三角形的公式.如果已知两角和一边,是否也有相应的直接解三角形的公式呢[3]?
探究2你能否根据图示(如图2),尝试推导上述公式(正弦定理)?

探究1从解三角形研究类型出发,在考虑到余弦定理可以解决的类型之外,比较自然地想到两角和一边是否有可以使用的公式,是从学生对问题的自然认识出发设计的.以课本为例,探究1通过特殊的三角形(直角三角形),利用正弦定理,对获得的式子作适当变形,猜想出正弦定理,但定理并非是利用探究的方法进行推理得到的.探究1只是告知问题研究的方向,没有给出问题的研究方法,很难获得需要的结论,即使学生在我们的引导下获得结论,学生的困惑还是会很大.
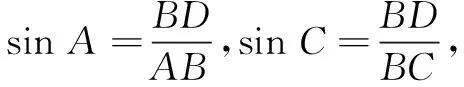
三、“二次探究”情境创设的注意点
1.情境设计要有目标
课堂二次探究情境应该针对的是这一节课中的核心问题(概念或命题)进行设计,正如案例1中的探究2,就是围绕本节课中的“平面与平面平行的性质定理”这一重点内容进行的设计,利用直线的变化得到不同结果,让学生在“变”中寻找共性.二次探究情境的创设,是在充分考虑学生第一次探究中可能出现的困难,重新设计研究方法,调整探究方案,进行再次探究.
2.探究要自然
探究2是探究1的自然延续.如案例1中的探究1是按以往学习的经验,对可能的结果进行的猜想,但探究的开放程度较大,无法得到课堂需要的结果.探究2给出探究的方法,让探究可以真正进行下去,两个探究之间是环环相扣的.案例3中探究1从特殊情况出发获得公式后,自然想到需要如何推理验证,探究2的出现也就水到渠成.
“二次探究”的自然性首先体现在情境与问题之间的自然,即所设计的情境能自然引出我们所需要的问题,问题的解决过程就是课堂新知识的获得过程;其次,“二次探究”一方面体现在新探究与上一次探究之间的自然衔接,另一方面体现在设计情境符合学生认识的自然,即“二次探究”应该是站在学生认知发展区内的探究.
3.探究要适度
探究与思考的区别一方面是情境所体现的学科素养水平,另一方面是问题的“度”,探究的“度”在于它给出制作“阶梯”的工具或指明可以找到更上一层楼的阶梯.如何更上一层楼,还要学习者进一步的探索.探究情境的适度是让学习者在其能力范围内有办法实现目标,是可以实现但不是轻易实现.
二次探究的“度”是教师在预计上一次探究可能出现困难,或没法达到知识学习深度的基础上,对探究重新设计情境,进行方法上的进一步启发.在实际教学中,还应根据课堂中出现的问题进行调整,如发现大部分同学有困难或方法出现偏离,可以给出适度的提示.

