借助勾股定理探求最短路径

詹静

勾股定理是几何中最重要、最基本的定理之一，也是求线段长度的有力工具，因此常被用于求最短路径的长.要借助勾股定理求几何图形中的最短距离，找出题目中正确的直角三角形是解题关键.下面分别探讨在平面图形中和立体图形中探求最短路径的方法.

一、运用勾股定理求平面图形中的最短路径

求平面图形中的最短路径问题，也就是求平面内几个点的距离之和最小值问题.解题通常要运用轴对称知识、三角形三边关系等，把问题转化为“两点间的最短距离”问题，再运用勾股定理进行计算.

例1某供电部门准备在输电主干线l上连接一个分支线路，分支点为M，同时向新落成的A、B两个居民小区送电.已知居民小区A、B分别到主干线l的距离AA1=2km，BB1=1km，且A1B1=4km.

（1）如果居民小区A、B在主干线l的两旁，如图1所示，那么分支点M在什么地方时总线路最短？最短线路的长度是多少千米？

（2）如果居民小区A、B在主干线l的同旁，如图2所示，那么分支点M在什么地方时总线路最短？此时分支点M与A1的距离是多少千米？

分析：（1）连接AB，构造直角三角形，由勾股定理求得AB的值；（2）作B点关于直线l的对称点B2，连接AB2交直线l于点M，此处即为分支点.

点评：在平面图形中，求最短路径问题通常是以“平面内连接两点的线中，线段最短”为原则，将分散的条件通过几何变换（平移或轴对称）进行集中，然后借助勾股定理求解出最值.

二、利用勾股定理求立体图形中的最短路径

解答立体图形中任意两点间的最短路径问题，应充分运用转化思想，将立体图形转化为平面图形，或将曲面转化为平面，从而把问题转化为平面内两点间的最短距离问题，然后通过构造直角三角形，运用勾股定理求解.

1.圓锥体中的最短路径

圆锥的侧面展开图是一个扇形，此类问题中没有直接的直角三角形，所以解题时要通过题目给出的数量关系构造出相应的图形，运用勾股定理计算.

例2如图3，圆锥的底面半径为1，母线长为3，一只蚂蚁从底面圆周上的点B出发沿圆锥侧面爬到过母线AB的轴截面上另一母线AC的中点D .问蚂蚁沿怎样的路线爬行，使路程最短？最短的路程是多少？

分析：将圆锥的侧面展开，根据“两点之间线段最短”可得出蚂蚁爬行的最短路线及最短的路程.

解：由题意知，圆锥底面圆的直径为2，故底面周长等于2π.

如图4，将圆锥的侧面展开，得到扇形BCB′，则蚂蚁沿线段BD爬行，路程最短.

设扇形BCB′的圆心角为n°，

2.圆柱体中的最短路径

圆柱的侧面展开图是长方形，要求圆柱体中的最短路径，首先要根据题意确定相应点的位置，然后连接相应点，构造直角三角形，利用勾股定理求解.

例3蜘蛛和苍蝇在一个圆柱面上，这个圆柱的高为10，底面的半径为4，如图5所示，AA′、BB′是圆柱的两条母线，蜘蛛在BB’上的P点，PB′=2，苍蝇在AA′上的Q点，QA=3，蜘蛛沿圆柱表面爬向苍蝇，求最短路程为多少？

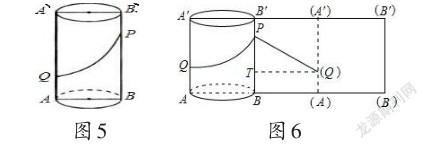
分析：要求不在同一个平面内的两点之间的最短距离，首先把圆柱的侧面展开，并连接两个点，然后分析展开图形中的数据，根据勾股定理即可求解.

3.台阶中的最短路径

台阶可以看成是多个长方体的组合图形，故要求出台阶中的最短路径，首先要正确求出展开后台阶整体的长度与宽度，然后运用勾股定理解答问题即可.

例4如图7，是一个三级台阶，它的每一级的长、宽和高分别等于5cm，3cm和1cm，A和B是这个台阶的两个相对的端点，A点上有一只蚂蚁，想到B点去吃可口的食物.请你想一想，这只蚂蚁从A点出发，沿着台阶面爬到B点，最短线路长是多少？

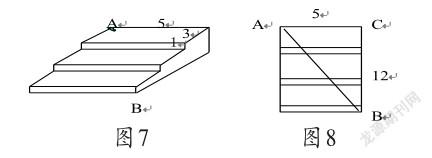
分析：由于蚂蚁是沿台阶的表面爬行，故只需要将台阶展开便可直观地得出解题思路.将台阶展开得到的是一个矩形，蚂蚁要从A点到B点的最短距离，便是矩形的对角线，利用勾股定理即可解出答案.

解：把三个台阶展开成平面图形，如图8.

由展开后的图形可知AC=5，BC=12，

在Rt△ABC中，∵AB2=AC2+BC2

即AB2=52+122=169，

∴AB=13.

故蚂蚁爬到B点的最短线路长是13cm.

点评：求解几何体的最短路线长，需把几何体适当展开成平面图形，在平面图形中将路程转化为两点间的距离，利用“两点之间线段最短”，或点到直线“垂线段最短”等性质并结合勾股定理来解题.

探求最短路径问题是初中数学中的一种常见问题.对这类问题，同学们应该学会分析、观察图形，灵活运用勾股定理，找出不同情况下的解题途径.