“长×宽”为什么等于“长方形的面积”

郜舒竹　李娟

【摘   要】在《义务教育数学课程标准（2022年版）》的课程目标中，对于“面积”这一课程内容要求“经历测量过程，探索计算方法”。长方形面积作为平面图形面积的认知起点，在数学课程内容中具有承上启下、不可或缺的地位。小学数学教科书通常把长方形面积公式表述为“长方形的面积=长×宽”，由此带来的问题是如何理解长度与长度的乘积等于面积。通过文献梳理得到的结论是，需要改变公式中长与宽作为线段长度的意义，将长与宽视为行与列，由此归纳出长方形面积测量的行列说。

【关键词】长方形的面积;面积;测量;计算;课程标准

我国小学数学课程内容中，“长方形的面积=长×宽”属于图形与几何领域中图形测量的内容。中华人民共和国教育部于2022年4月21日颁布的《义务教育数学课程标准（2022年版）》（以下简称《2022年版课标》）中，将这一内容安排在第二学段（3～4年级），学段目标描述为“经历平面图形的周长和面积的测量过程，探索长方形周长和面积的计算方法”[1]。为了将“经历”与“探索”的活动落实到教材编写以及教学实践中，首先需要明晰长方形面积“测量过程”的意义以及主要环节。其核心问题是：“长×宽”为什么等于“长方形的面积”？

一、“测线算面”的历史传承

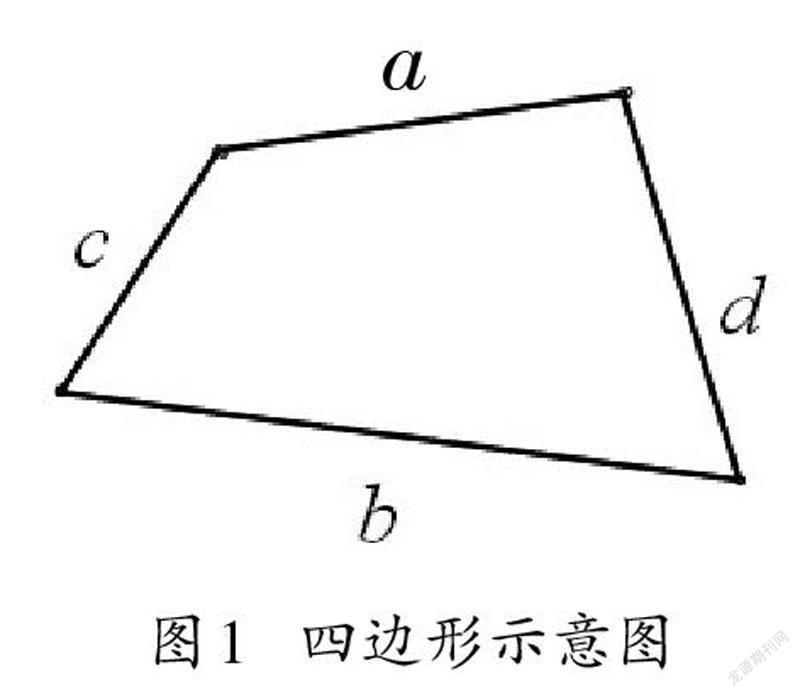
从历史发展的角度看，平面图形面积的测量与计算源远流长，距今约4000年（公元前1900年）的古巴比伦时期留存下来的纸草书中就有记载，基本的做法是用图形边界线的长短及其运算粗略地估计面积的大小。比如对于任意四边形，就用相对边长度平均值的乘积表达这个四边形的面积。[2]

图1中四边形面积用相对边长度的平均值的乘积表示为a+b/2×c+d/2。对一般的四边形来说，这样的做法只是近似的估计。但对长方形来说，这樣的做法就是准确的计算，长方形相对边的长度相等，即“a=b，c=d”，a+b/2×c+d/2的计算就相当于“长方形的面积=长×宽”。

像这样利用平面图形边界线长度计算图形面积的想法和做法流传至今，对平面图形面积大小进行估计或计算，首先要测量平面图形边界线的长度，然后通过计算得到平面图形的面积。这样从测量长度到计算面积的过程与方法，我们简称为“测线算面”。

线段长度的测量相对直接、便捷，用一根小棍或线绳，甚至身体上的臂长、脚长、步行时的步幅等，都可以实现对长度的测量。我国历史上的长度单位“寸、尺、丈”以及英制长度单位“Foot”等，都具有这样的具身性。平面图形面积的测量相对于长度，就不具有这样直接、便捷的特征。因此自然的想法和做法就是利用“测线算面”获得面积。

从方向的角度看，线段的长短仅从前后、左右、上下、高低、深浅这样单一方向就可以确定，因此是一维测量。而长方形面积的大小仅从单一方向无法确定，需要通过两个不同方向的测量共同确定，如果横向测量的是长度，那么纵向的测量就是宽度，因此长方形面积的测量是二维的。

从“量纲（Dimension）”的角度看，长度与面积作为几何中的量，维度不同，自然就属于不同的类型。如果把米、分米、厘米等描述长度的单位叫作“基本单位（Primary Unit）”，那么平方米、平方分米、平方厘米等描述面积的单位，就成为从基本单位构造出来的导出单位或“衍生单位（Derived Unit）”[3]。因此从课程体系来说，“长方形的面积=长×宽”这一课程内容，是从一维测量的认知跨越到二维测量认知的转折点，是从基本单位构造导出单位的认知起点，在课程内容体系中具有承上启下、不可或缺的重要地位。

长方形的“长”和“宽”，从“形（Form）”的角度看是线段，从“量（Magnitude）”的角度看是线的长度，这里的长度，不是用数表达的，而是直觉中的长短。因此，作为运算的“长×宽”具有双重意义，第一是将一维的线段变成了二维的长方形，也即“变线为面”;第二是“变长度为面积”，两个同类的量（长度）相乘，衍生了不是长度的另外一类量（面积）。

因此“长×宽”中的运算符号“×”具有质变的功能，这样的功能是加、减运算所不具备的，长度与长度相加或相减的结果还是同类的长度，不可能改变为非长度的其他量。凡此都体现出作为乘法运算的“长×宽”等于长方形的面积，并非自然而然、顺理成章的，需要对“长度×长度”的意义做进一步的理解。

二、“长度×长度”未必是面积

人们日常经验中所说的“远近、高低、长短、宽窄、深浅”等，都属于“长度（Length）”的范畴，长度这一概念源于对线段的感知与想象。将空间中两个位置不同的对象（比如两棵树），想象为两个“点（Point）”，这里所说的点不是真实存在的对象，是人心智中生成的对象，是想象出来的思维对象。罗马尼亚著名数学教育家、数学教育心理学会（PME）创始人菲茨拜因（Efraim Fischbein，1920—1998），把这样想象出来的对象叫作“比喻概念（Figural Concept）”[4]，其意义为借此说彼。比喻概念具有无中生有的想象性或虚拟性特点，是对具体对象的抽象，把一棵树视为一个点，忽略了形状、大小、高低、材质等因素，只保留了空间位置的属性。《2022年版课标》把这样的认知过程归属为“用数学的眼光观察现实世界”。

为了描述这样想象出来的点之间的关系，自然就生成了线段的概念，这样的线段未必是真实存在的，同样是想象出来的比喻概念，借以描述两个空间位置之间的关系。通过这种线段的诸多比较，就可以意识到长与短的相对关系。线段长与短的差异，是客观存在、可感知的现象，像这样客观存在，具有程度差异，并且可合可分的现象，称为几何中的“量”，也叫作“广延量（Extensive Quantity）”[5]。

这时并没有指定一个类似于“厘米”的确定的单位，因此这时的长度并不能用数表达，只能通过直觉比较不同长度的长短。如果需要用语言表达某条线段的长度，可以用类似于字母的符号，比如线段AB的长度为a，这里的字母a表达的不是数，而是作为量的长度（如图2）。

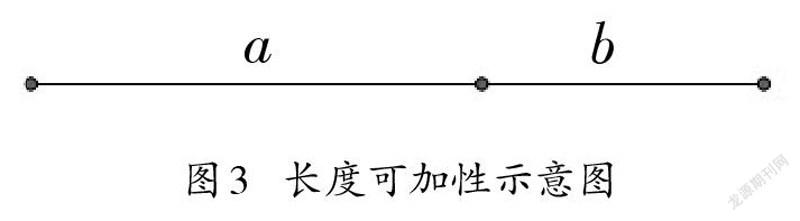
作为量的长度之间的关系决定了其作为数学研究对象的逻辑基础。如果说一条线段与另外一条线段长度相等，那么就排除了不相等的情况。同样，如果一条线段比另外一条线段长，那么两条线段长度就不可能相等。简单说，两条线段的长度a与b之间的关系只能是下面三种情况之一：a=b;a>b;a<b。不可能出现“同时相等和大于;同时大于和小于”等情况，这样的关系数学中通常叫作“单调（Monotone）”关系或“序（Order）”关系。几何中的广延量另外一个性质是“可加性（Additivity）”，也就是可分可合的性质，区别于温度、浓度、速度等“强度量（Intensive Quantity）”的不可加性[6]。可加性使得线段的长度可以实施加、减运算，比如长度为a的线段与长度为b的线段，拼接为一条新线段，其长度可以表示为“a+b”（如图3）。

同样“a-b（假定a>b）”可以表示从“a”中截取“b”后剩余部分的长度，也可以是a比b多出来的部分。除了加、减运算，还可以用“比（Ratio）”描述长度a与长度b的关系。按照欧几里得《几何原本》中对比的定义，如果a>b，用b重复量a，重复若干次后，可以超出a的长度，就说a与b之间存在着比。[7]这是纯粹的量之间相互比较的过程，类似于算术中的除法运算。

总之，线段长度的运算可以有加、减和类似于除法的比，其中的运算所指对象不是数，而是作为线段长度的量，因此运算的意义不是针对数的计算，而是针对量的“操作（Operation）”，线段的拼接、分割、重复度量等都可以视为这样的操作。这样的操作具有具身性和可感知性，是伴随着人“拼接、分离、重复”等动作而发生的，是具有实际意义的。

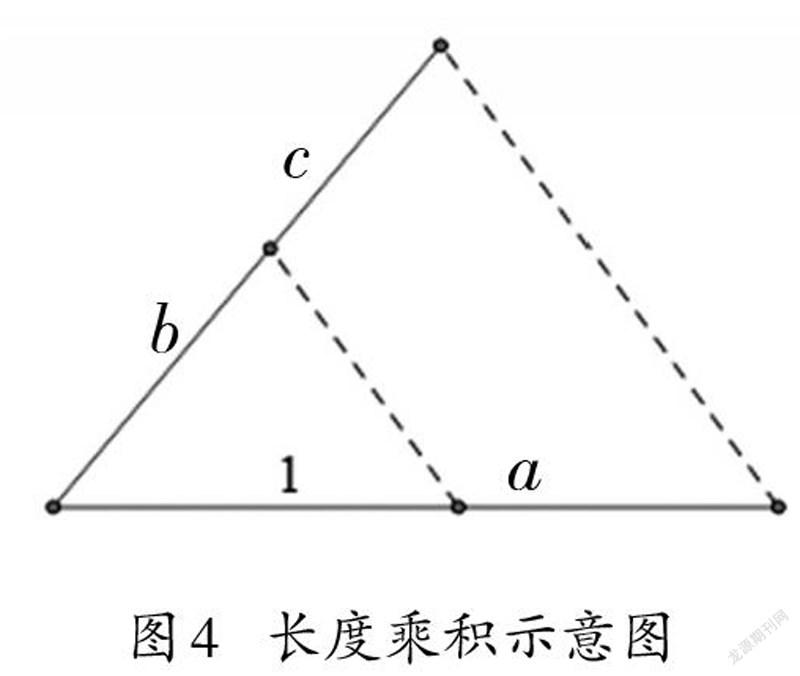
接下来的问题是：作为量的长度是否可以定义类似于算术中的乘法运算？也即“长度×長度”是否具有实际意义？ 17世纪法国著名哲学家、数学家勒内·笛卡尔（René Descartes，1596—1650）认为，几何中线段长度的乘法是可以定义的，两条线段长度相乘的结果仍然是线段的长度。[8]

图4中一个大三角形内有一个小三角形，两条虚线相互平行。利用两个三角形的相似关系可以知道，大三角形与小三角形对应边长度之比相等，即“c∶b=a∶1”。历史上，人们将“乘”的运算视为“造（Produce）”的过程，“a×b=c”中的a和b通过运算“造”出一个新的量c，这个造出来的c需要满足一个比例关系，即“c与a的比，等于b与1的比”。或者，“c与b的比，等于a与1的比”。笛卡尔利用平行线之间的比例关系，得到“c∶b=a∶1”，进而通过比例的基本性质得到“a×b=c”，也就是长度分别为a与b两条线段的乘积，得到另外一条长度为c的线段，表示为“a×b=c”。

由此看出，两条线段长度的乘积，未必得到平面图形的面积。也就是说，如果把长方形的长和宽看作两条线段，二者长度的乘积等于长方形面积，并不是自然而然的。

三、“厘米×厘米”的窘境

如果指定一条固定线段的长度作为单位，这时任何一条线段的长度相对于这个单位的比就成为用数表达的长度。比如把固定线段的长度“1厘米”当作长度单位，另外一条线段的长度包含3个1厘米，那么这条线段的长度就可以用数表示为“3厘米”，其意义是包含有3个1厘米，或将1厘米长度的线段拉长为原来的3倍。

像“3厘米”这样用数表达量的方式，不同于单独写出的数“3”。“3”只是个“数字符号（Numeral）”，不确定“1”的意义，就无法确定“3”的意义。而“3厘米”对应的单位是“1厘米”，由于1厘米具有确定的意义，3厘米也随之具有确定的意义了。类似于“3厘米”这样，用带有确定单位的数表达量的方式，我国历史上叫作“名数（Denominate Number）”，与之相对的叫作“不名数（（Indenominate Number））”或“无名数”。

由中国图书公司出版的《最新算术教科书》中，对名数与不名数的描述分别是“凡数系以单位之名者，曰名数。不系以单位之名者，曰不名数”[9]。因此所谓名数就是带有单位的数，不名数就是不带单位的数1。由于名数具有具体的实际意义，因此在国外许多文献中也叫“具体数（Concrete Number）”，不名数相对于名数更加抽象，也叫“抽象数（Abstract Number）”[10]。

如果用厘米作为长度单位，那么“长方形的面积=长×宽”中的长和宽，都可以表示为以厘米为单位的名数，因而使得“长×宽”成为两个以厘米为单位的名数的乘积，简写为“厘米×厘米”，其结果成为以“平方厘米”为单位的名数。此时“长方形的面积=长×宽”中的乘法运算，成为两个相同长度单位名数的运算，运算结果产生了一个不同于长度单位的新的单位，命名为“平方厘米（Square Centimeter）”，意为“边长为1厘米的正方形”。

在之前二年级认识乘法时，是把乘法理解为“相同加数求和”或“求一个数的几倍”的运算。比如“3×2”，其中的“3”和“2”具有不同的意义，如果“3”表示“3个苹果”，那么“2”就不能表示“2个苹果”，人的实际经验中并不存在“苹果×苹果”的实际意义。“3个苹果×2”中的“2”，可以是数数过程的“次数”，也可以是每个盘子中有3个苹果的“盘数”等，是表示将“3个苹果”重复的次数，可以统称为“倍”。像这样表示倍的数，相对于表示苹果的个数而言，并不指向具体的对象，具有抽象的意义，可以看作是不名数或抽象数，因此“倍”的实质是给乘法运算中的不名数赋予了一个统一的名称，表达重复的次数，相当于英文中的“Time”。

二年级学生对于乘法算式先入为主的经验是“名数×不名数”，或“具体数×抽象数”。把这样的经验应用于长度的测量，“3厘米×2”的意义是把“3厘米”长度的线段看作一个整体，用这个3厘米长度作为单位，去测量另外一条更长的线段，测量动作重复了2次，测量的结果包含了2个3厘米，其中“3厘米×2”中的两个因数“3”和“2”意义不同，前者“3”是名数或具体数，后者“2”是不名数或抽象数。

如果一个长方形相邻两边长度，也就是长和宽的长度分别为3厘米和2厘米，那么按照“长方形的面积=长×宽”，这个长方形面积应当写为“3厘米×2厘米”。其中的3和2都带有共同的单位“厘米”，都是具体的名数。沿用前面乘法的经验，“将3厘米重复2厘米次”，显然是说不通的。

英国19世纪著名数学家奥古斯都·德·摩根（Augustus De Morgan，1806—1871）在《代数学原本（Elements of Algebra）》一书前言中，把这样“厘米×厘米”的情况称为“荒诞的（Absurd）”[11]。美国数学教育家、著名数学期刊《美国数学月刊》创始人本杰明·富兰克林·芬克尔（Benjamin Franklin Finkel，1865—1947）甚至认为，将长方形的面积写为“长×宽”是“错误的（Wrong）”，数学中没有相应的法则做出这个判断。如果“厘米×厘米=平方厘米”（原文中用的是“英尺”）正确，那么也应当有“美元×美元=平方美元”，这显然是不合逻辑的。[12]

综上可以看出，从线段长度“量”与“数”的意义以及二年级学生对乘法的认识中，无法直接得到“长方形的面积=长×宽”这一等式，其中“×”的意义与之前的经验“不一致（Inconsistence）”。把“长方形的面积=长×宽”中的“长”与“宽”看作线段的长度，无法与之前所熟悉的乘法意义形成一致性的认识，这就使得“测线算面”的认知过程出现了障碍。

四、“长×宽”的意义改变

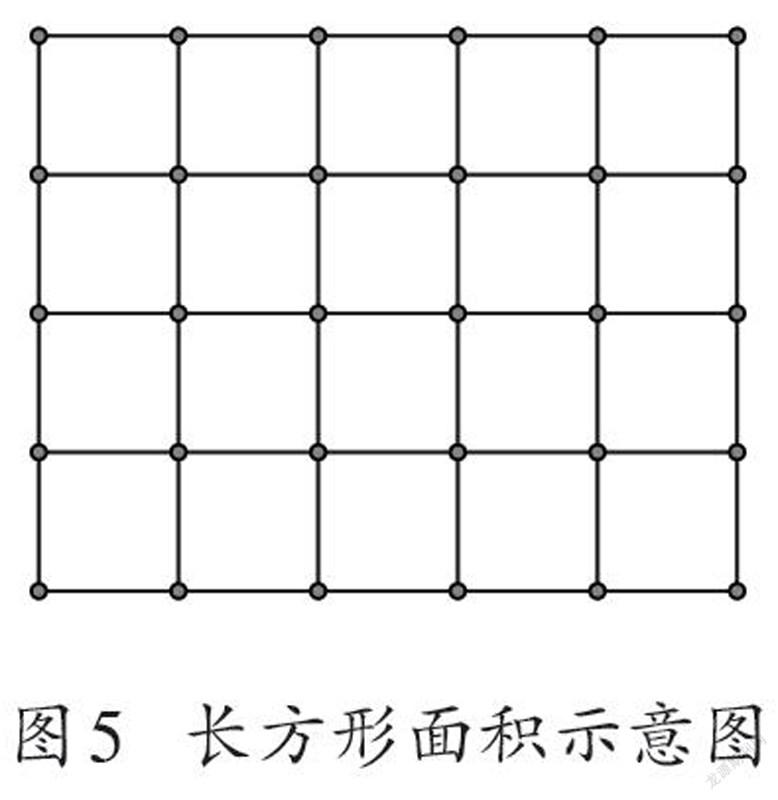
美国19世纪数学家阿尔伯特·泰勒·布莱德索（Albert Taylor Bledsoe，1809—1877）在《数学哲学》一书中，对长方形面积公式做过如下解释：一个长方形长和宽的长度分别为5英尺和4英尺，5英尺与4英尺两个名数相乘并不直接等于长方形面积。首先将两个以英尺为单位的名数改变为没有单位的不名数5和4，而后对两个不名数实施乘法计算“5×4=20”，这个乘积20仍然是不名数，不代表长方形，也不是长方形面积，但这个20恰好与长方形中边长为1英尺的小正方形个数相等，如果把边长为1英尺的正方形的面积命名为“1平方英尺”，那么长方形面积恰好等于20个1平方英尺，而且这样的过程普遍适用于所有长方形的情况。[13]

这一解释实际上是用边长为1英尺的小正方形对长方形进行密铺，先横向看每行有5个小正方形，再纵向看一共有4行（或先纵向看每列有4个小正方形，再横向看共有5列），因此小正方形个数为“5×4=20”。这时是将数字“5”视为横向的“5个小正方形”，而不是5英尺;其中的数字“4”也不是4英尺，而是将每一行的“5个小正方形”看作整体，称之为“1行”，共有4个这样的整体，也就是4行（如图5）。

这就表明长方形面积公式中“长×宽”的意义，不是两条线段长度的乘积，而是行数与列数的乘积，简写为“行×列”。首先确定边长为1英尺的正方形面积为1平方英尺;其次沿着一个方向数出“5个1平方英尺”，或1平方英尺放大为原来的5倍，也即“1平方英尺×5”;最后将“5平方英尺”沿着另一方向重复4次。这样的过程与“5英尺×4英尺”的意义不同，其中的因数5是将“1平方英尺”重复5次，因数“4”是将“5平方英尺”重复4次，因此因数5和4都具有不名数的意义。按照布莱德索的观点，“5英尺×4英尺”的真实意义是两次乘法运算的合成，可以表示为：

1平方英尺×5=5平方英尺

5平方英尺×4=20平方英尺

美国纽约州皮尔森教育公司于2019年出版的《中小学数学发展性教学》一书的第10版中，沿用了布莱德索的解释，特别强调长方形面积公式“长×宽”中的长与宽，表示的不是长度。“长方形的面积=长×宽”并非表达长度与长度的乘积等于面积，而是行数与列数的乘积等于面积，即“长方形的面积=行×列”。[14]这时“×”的意义与“相同加数求和”或“求一个数的几倍”就具有了一致性。

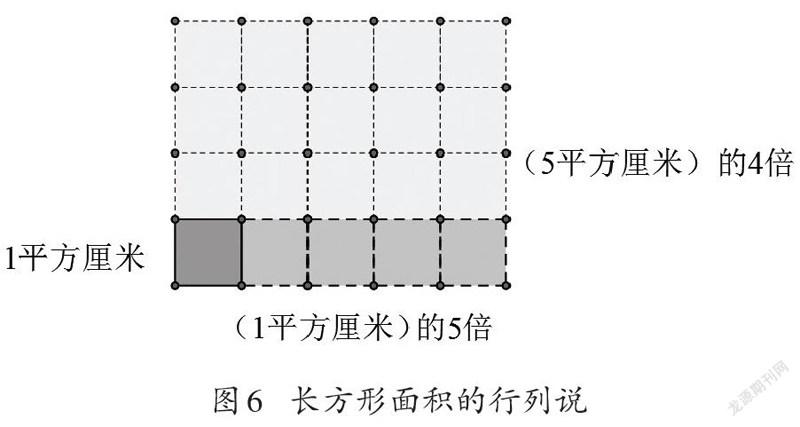
对于长为5厘米、宽为4厘米的長方形，首先确定边长为1厘米的正方形面积为“1平方厘米”，长度为5厘米的边上就对应了“5个1平方厘米”的小正方形。这一行中小正方形个数就是1平方厘米的5倍。而后将这一行的5个小正方形在行的方向上排成4行，成为一行“5平方厘米的4倍”（如图6）。

这种行列说改变了“长”与“宽”线段及其长度的意义，强调其方向的意义，即作为面积单位的小正方形在两个不同方向延展的意义，因此长方形面积的测量过程可以概括为以下三个步骤。

确定作为面积单位的小正方形。

沿着同一方向延展面积单位，从而确定包含面积单位的“行（或列）”。

把这样的“行（或列）”看作整体，沿着另一方向延展，进而确定“行数（或列数）”。

“长方形的面积=长×宽”的解释，将其中乘法运算的意义与学生已有经验建立起了一致性的联系。这一解释的前提是把长和宽的长度表示为整数，基于对面积单位进行“数数（Count）”的认知活动。因此行列说并不能涵盖长方形面积公式的全部意义，随着数学课程内容中数系的拓展，这一公式的意义与作用也会随之进化与拓展。行列说仅适用于对长方形面积公式的初步认识。

五、进一步的问题

综上所述，面积本质上是一类几何中的广延量，表现为有限平面区域的大小。区别于单一方向一维线段的长度，面积的测量需要用二维的眼光，即不同方向的观察与操作。沿袭历史上“测线算面”的传统，自然的想法和做法是建立平面图形的面积与其边界线长度之间的关系，并且能够运用算术中的计算实现用长度计算面积的目的。

对于长方形而言，其形状和大小随着长和宽长度的给定而确定，这样的关系使得利用长和宽的长度计算长方形的面积成为可能。为了实现这样的可能性，就需要确定面积单位，而后从长和宽两个方向用面积单位铺满长方形，进而长方形就成为已作为面积单位的正方形组成的“行列结构（Arrays）”，行列结构中的行数与列数的乘积恰好等于面积单位的个数，从而得到长方形的面积。

测量过程的第一步是确定作为面积单位的正方形，是实现面积测量与计算的起点。《2022年版课标》学段目标中的“测量过程”自然应当包括这样确定面积单位的过程。如果用长度为1厘米的线段表示长度单位，那么以上测量过程的第一步就是确定边长为1厘米的正方形面积为面积单位，确定面积单位的过程实质是人为地作出了三项规定。

第一，作为面积单位的图形是正方形。

第二，作为面积单位的正方形边长是1厘米。

第三，面积单位表示为1平方厘米或1厘米。

数学课程中诸如此类的内容具有“人为规定”的属性[15]，区别于通过演绎推理所获得的“必然真（Necessary Truth）”的判断，确定单位往往具有未必如此的“任意性（Arbitrary）”特点[16]。针对这样的内容，自然期望学生能够用差异的眼光观察、多元的思维思考、个性的语言表达。因此教科书编写以及教学过程中仅有“是什么”的问题是不够的，还需要有“为什么是……”以及“为什么不是……”的思考与交流[17]。如：

作为面积单位的图形为什么是正方形？而不是其他图形？

作为面积单位的正方形，为什么边长是“1”，而不是其他数？

为什么把“1平方厘米”表示为“1厘米”？

《2022年版课标》倡导要让学生经历“发现问题和提出问题，分析问题和解决问题”的全过程，因此对于长方形面积的教学目标仅指向“会计算”是不够的，要让诸如此类的问题融入教材的教学内容以及实际教学中，让学生有机会亲身经历面积测量的全过程。为此就需要对这些问题作进一步的思考和研究，在此基础上，努力为学生设计出更加丰富、有效的认知活动，真正实现素养导向的数学教学。

参考文献：

[1]中华人民共和国教育部. 义务教育数学课程标准（2022年版）[M]. 北京：北京师范大学出版社，2022.

[2]DODD W A. The history of mensuration[J]. Mathematics in School， 1977， 6（4）： 8-9.

[3]郜舒竹.看“一”的眼光[J].教学月刊·小学版（数学），2020（11）：4-8.

[4]FISCHBEIN E. The theory of figural concepts[J].Educational Studies in Mathematics， 1993， 24（2）： 139-162.

[5]蒋鑫源，郜舒竹.“数”与“量”的意义辨析[J].教学月刊·小学版（数学），2021（9）：4-6.

[6]吕港丽，郜舒竹.“强度量”的意义与认知规律[J].教学月刊·小学版（数学），2021（12）：4-9.

[7]郜舒竹.释“比”[J].教学月刊·小学版（数学），2021（6）：4-8.

[8]OSTERMANN A， WANNER G. Geometry by its history[M]. Berlin： Springer， 2012： 160.

[9]石承宣. 最新算术教科书[M]. 上海：中国图书公司，1907：1-2.

[10]WOOD. On the use of the term abstract in arithmetic [J]. General Report （Association for the Improvement of Geometrical Teaching）， 1891， 17（1）：10-22.

[11]MORGAN A D. Elements of Algebra [M]. London： Bookseller and Publisher to the University of London， 1835：19.

[12]FINKEL B F. A mathematical solution book [M]. Washington： Kibler & Company， Publishers， 1899：261.

[13]BLEDSOE A T. Philosophy of Mathematics [M]. Philadelphia： J. B. Lippincott Company 1886：95.

[14]JOHN A， WALLE V D， KAREN S. Elementary and middle school mathematics teaching developmentally： Tenth edition [M]. New York： Pearson Education，2019：503.

[15]郜舒竹.數学课程中“人为规定”的思想性[J].课程·教材·教法，2018（9）：93-98.

[16]HEWITT D. Arbitrary and necessary part 1： a Way of Viewing the Mathematics Curriculum[J]. For the learning of Mathematics，1999，19（3）：2-9.

[17]郜舒竹.“平行四边形面积”之难[J].教学月刊·小学版（数学），2020（1/2）：4-7.