贝叶斯方法在大跨度斜拉桥模态参数识别中的应用研究

杨朝勇，茅建校，王 浩，张一鸣

（东南大学混凝土与预应力混凝土结构教育部重点实验室，江苏南京 211189）

引言

模态参数是开展桥梁振动控制、状态评估和损伤诊断的重要依据，在桥梁结构健康监测中发挥着关键作用［1］。在运营结构的模态参数识别中，由于材料的离散性、模型误差以及测试噪声等原因，分析结果不可避免地具有不确定性［2］。大跨度桥梁属于典型的低频密集模态结构，相比于一般结构更加难以准确地获取其模态参数［3］。尤其是沿海地区的大跨度桥梁，时常受到台风等极端天气袭击，其动力性能面临的不确定因素更加显著［4］。因此，为了给大跨度桥梁健康监测提供稳定可靠的分析依据，有效评估模态识别结果的不确定性至关重要［5］。

贝叶斯方法是近些年兴起的一种不确定性分析技术。该方法认为识别结果的不确定性与模态参数在给定的振动数据和假设模型下的条件概率密度函数（PDF）有关［1］，因此可以根据概率模型中的最大概率值（MPV）与协方差矩阵进行模态参数识别与不确定性量化。目前，在贝叶斯理论框架下已经发展出了多种模态参数识别方法［6-8］。其中，Au［9］提出的快速贝叶斯快速傅里叶变换（FBFFT）法受到了广泛的关注。该方法简化了模态参数似然函数的内部结构，避免了目标函数维度过高导致求解困难的问题。此外，FBFFT 法在分离模态［10］和密集模态［11］下均能取得良好的识别结果，能够适用于各种土木工程结构的动力特性分析［12-13］。

根据目标函数优化求解MPV 是贝叶斯模态参数识别方法的关键，确保该过程的稳定性和计算效率至关重要。遗传算法是一种不依赖目标函数梯度信息的启发式智能优化算法，能够很好地适应高维度、多参数的优化问题［14］。应用遗传算法求解最优模态参数，可有效地提升模态参数识别的稳定性与可靠性［15］。但相比于牛顿迭代法、梯度下降法等传统优化算法，遗传算法对计算机算力要求较高［16］。因此，要将遗传算法与贝叶斯方法结合，仍需针对两者特点研究相应的加速策略，以满足大跨度桥梁运营模态分析对计算效率的要求。

鉴于上述问题，本文结合FBFFT 法和遗传算法发展了一种考虑不确定性的大跨度桥梁模态参数识别方法。该方法在FBFFT 法中引入遗传算法搜寻最优参数，并基于高信噪比假设［17］建立渐进估计区间，以进一步提升桥梁模态参数识别与不确定性量化的效率与可靠性。本文首先利用一个6 自由度悬臂梁模型验证上述方法的识别精度与效率；然后以苏通大桥为例开展大跨度斜拉桥的模态参数识别与不确定性评估，并在此基础上分析频带宽度系数对识别结果的影响以及模态参数PDF 的分布特征。

1 基于贝叶斯-遗传算法的模态参数识别方法

1.1 FBFFT 法

具有n个通道的一组实测加速度信号可以表示为系统真实响应与预测误差的和，即：

式中xj=｛x1j，x2j，…，xnj｝表示实测信号；yj=｛y1j，y2j，…，ynj｝表示受模态参数θ影响的实际振动信号，其中θ包含频率f、阻尼比ζ、模态力功率谱密度Sl、预测误差功率谱密度Se以及振型向量Φ；ej=｛e1j，e2j，…，enj｝表示预测误差；j=1，…，N，N为样本数量。xj的傅里叶变换可表示为：

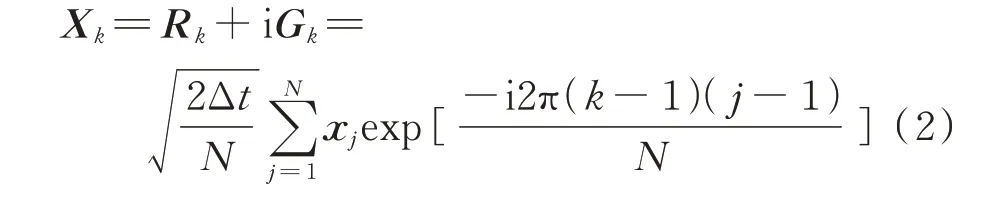
式中Rk与Gk分别表示Xk的实部与虚部；Δt是采样时间间隔；Xk实质是对xj的快速傅里叶变换（FFT）进行倍缩放，因此Xk又被称为缩放FFT（Scaled FFT，SFFT）。

Rk与Gk构成的随机向量k=2，…，Nq，Nq=int（N/2）+1｝服从零均值多元高斯分布，且各频率点间相互独立［6］。因此，θ的似然函数可表示为：

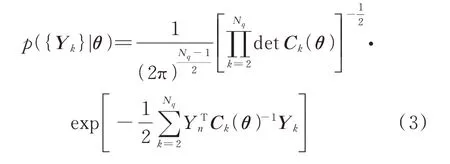
式中Ck为Yk的协方差矩阵，可表示为：

式中 I2n为2n×2n阶的单位矩阵；βk=f/fk，fk表示Yk对应的频率。

根据贝叶斯定理，θ关于Yk的后验PDF，p（θ|｛Yk｝）与p（｛Yk｝|θ）之间满足如下关系：

式中p（θ）是关于θ的先验PDF，一般视为常数。

忽略常数项，上式可进一步用对数似然函数表示为：

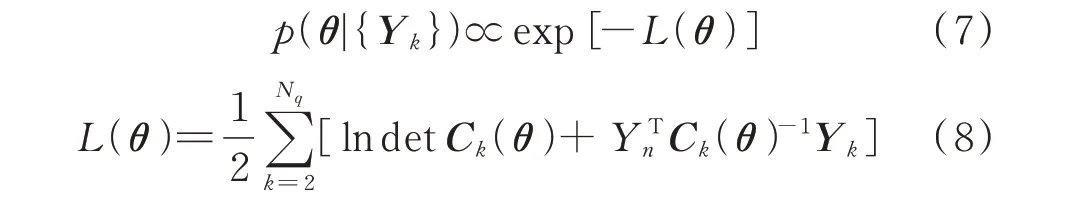
模态参数的MPV 可通过求解式（8）的对数似然函数的最小值确定。

1.2 遗传算法与渐进估计区间

遗传算法以目标值的适应度作为个体优劣性的评价指标，并按一定概率随机执行个体的选择、交叉与变异，从而在不断迭代更新的种群中搜寻最优参数。该方法具有突出的全局寻优能力与稳定性，能够很好地处理高维空间参数优化问题。因此，本文将遗传算法引入FBFFT 法中开展对数似然函数优化，以确保模态参数识别结果的准确性。

参数优化过程的收敛速度对模态参数识别至关重要。遗传算法虽然具有较好的鲁棒性，但相比于梯度下降法、牛顿迭代法等传统优化算法该方法计算效率较低［18］。因此，为了克服遗传算法收敛速度上的不足，本文引入高信噪比假设建立渐进估计区间。把遗传算法参数搜索范围约束到最优值附近，从而加快模态参数识别效率。

根据文献［10］，当结构振动信号的信噪比很高时，振型向量Φ可由矩阵A0的最大特征值λ0对应的特征向量渐进估计：

预测误差与模态力功率谱密度可按下式估计：

式中Nf表示提取出的SFFT 样本数量。

当对数似然函数L（θ）关于｛Φ，Se，Sl｝最小化后可进一步被简化为如下形式：

由于环境等因素，桥梁结构振动监测数据中往往混有大量噪声，难以满足高信噪比条件。本文虽然利用高信噪比假设约束了遗传算法的参数搜索空间，但由于优化模型中并未考虑高信噪比假设，最终结果中并不包含任何渐进估计成分。因此，该方法能够用于大跨度桥梁健康监测数据的分析。

1.3 后验不确定性

在足够大的数据量下，后验PDF 可用一个等价于L（θ）二阶导数的高斯PDF 渐进估计［17］。特别地，将L（θ）在处二阶泰勒展开有：

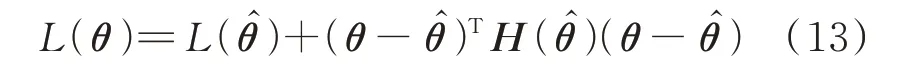
由式（13）可知，L（θ）的Hessian 矩阵等于协方差矩阵C的逆矩阵。研究表明［9］，L（θ）在振型向量Φ的方向上导数为零，Hessian 矩阵必然存在对应特征向量是［0 0 0 0ΦT］的零特征值。因此，Hessian矩阵不可逆。

假设｛λ1，λ2，λ3，…，λn+4｝是Hessian 矩阵的特征向量｛v1，v2，v3，…，vn+4｝所对应的特征值。令λ1=0，忽略该零特征值项。根据Hessian 矩阵的实对称矩阵特性，Hessian 矩阵的逆矩阵，即后验协方差矩阵可由下式计算：

得到协方差矩阵后，模态参数的不确定性可由对应的变异系数（c.o.v=标准差/MPV）量化。此外，振型的不确定性可用下式表示：

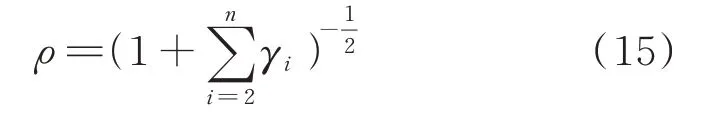
ρ被称为期望模态置信准则（MAC）［19］，ρ越接近于1，振型的不确定性越低；γ表示协方差矩阵中关于振型向量的n阶方阵的特征值（忽略i=1 对应的零特征值项）。

1.4 计算流程

为便于表达，将所使用的方法统称为贝叶斯-遗传算法。首先对加速度信号进行SFFT 变换，然后以频谱峰值为中心按f0（1±0.01κ）的宽度选择样本数据。f0表示频谱峰值对应的频率，可按功率谱密度（PSD）谱或奇异值（SV）谱峰值确定；κ为频带宽度系数。在获得样本数据后，便可利用贝叶斯-遗传算法识别各模态参数并量化其不确定性。主要的计算流程如图1所示，其中贝叶斯-遗传算法优化模型的种群个体数为50，交叉与变异概率分别为0.7与0.01。

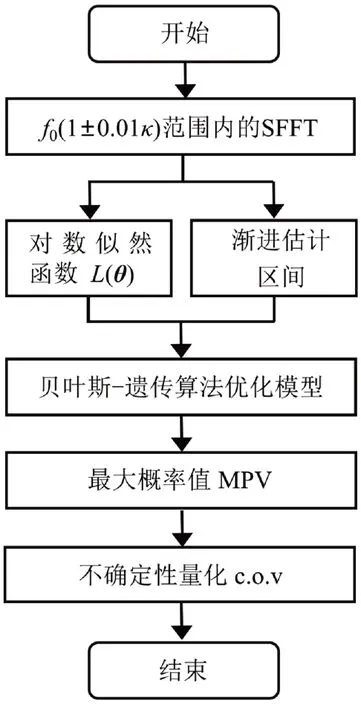
图1 计算流程图Fig.1 Flowchart of calculation

2 数值算例

本节采用6 自由度悬臂梁模型验证贝叶斯-遗传算法的识别精度与效率，如图2所示。该模型所有质点的质量均为1000 t，质点间的竖向剪切刚度为750×103kN/m，且各阶模态阻尼比均为0.05。悬臂梁模型前三阶模态的自振频率理论值分别为1.05，3.09 和4.95 Hz，本节对此三阶模态进行参数识别。以高斯白噪声为激励计算悬臂梁模型的加速度响应，采样频率为50 Hz。在每个质点处采集到65536 个加速度数据，并在其中添加均方根为无噪声模拟数据20%的高斯白噪声模拟预测误差。

图2 6 自由度悬臂梁Fig.2 Cantilever beam with 6-DOF

悬臂梁模型的模态参数识别结果与对应的理论值如表1 与图3所示。此处还采用频域分解（FDD）法进行了振型识别，以对比两种方法的识别精度。由表1 与图3 可知，FBFFT 法识别的各模态参数与理论值十分接近，仅存在微小的误差。由FBFFT法识别的振型与理论振型吻合良好，且各阶振型的ρ都近似于1，振型不确定性较小。FDD 法识别出的振型同样具有较高精度，但相比之下，FBFFT 法识别振型的MAC 值比FDD 法识别振型的MAC 值更接近于1，FBFFT 法精度更高。

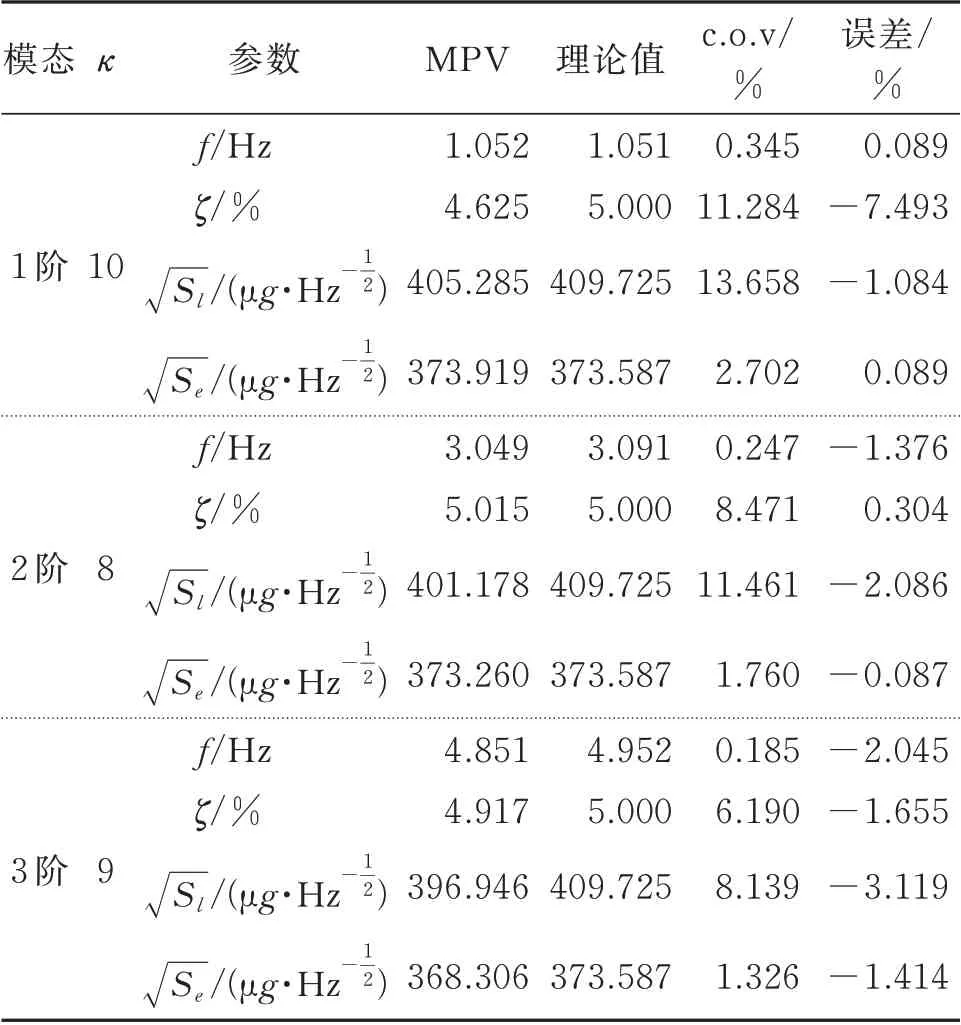
表1 数值模型参数识别结果Tab.1 Model parameters identified results of numerical model

图3 悬臂梁振型识别结果对比Fig.3 Comparison of mode shapes identified result

为验证渐进估计区间对提升模态参数识别效率的有效性，利用不同方法对一阶模态对数似然函数进行优化，计算迭代过程如图4所示。其中大区间搜索遗传算法不使用渐进估计区间，而是在包含了可能模态参数值的大区间内搜寻最优值。该区间根据经验确定，本节频率区间设为［0.8f0，1.2f0］，阻尼比区间设为［0.5%，7.5%］，模态力功率谱密度与预测误差谱密度区间均设为［0，0.5 m2/（s4·Hz）］。Nelder-Mead 法是一种能够很好地适应多参数优化问题的局部寻优算法，在适当的初值下具有精度高、计算快的特点。该方法在FBFFT 法中的迭代初值可参见文献［10］。

由图4 可知，在渐进估计区间寻优的遗传算法能够很快收敛，而Nelder-Mead 法的迭代次数略多于渐进估计区间搜索遗传算法。相较于渐进估计区间搜索遗传算法与Nelder-Mead 法，大区间搜索遗传算法计算速度明显变慢，需要更多迭代次数。在迭代次数达到100 时，渐进估计区间搜索遗传算法与Nelder-Mead 法早已收敛，但大区间搜索遗传算法仍未到达最优值。因此，高信噪比渐进估计区间能够有效提升模态参数识别效率，并避免遗传算法陷入局部最优解。需说明的是，此处仅考虑了单个模态下的参数优化，各方法计算耗时均较短。因此，本节没有进行详细的计算时长对比。

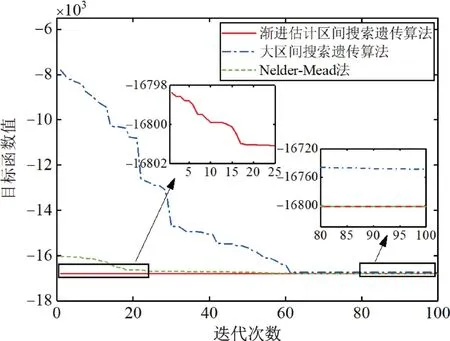
图4 不同优化方法迭代过程Fig.4 Iterative process of different optimization methods

3 大跨度斜拉桥模态参数识别

苏通大桥主跨长度1088 m，是世界首座千米级斜拉桥。该桥建立了全面的健康监测系统，其中主梁加速度传感器的布置如图5所示。每个传感器布置截面均包含左右幅两个竖向加速度传感器，采样频率为20 Hz。本节采用安装于主跨的5 对加速度传感器（ACC-3#～ACC-7#）的监测数据开展苏通大桥运营模态分析，每个通道的样本数量为72000。

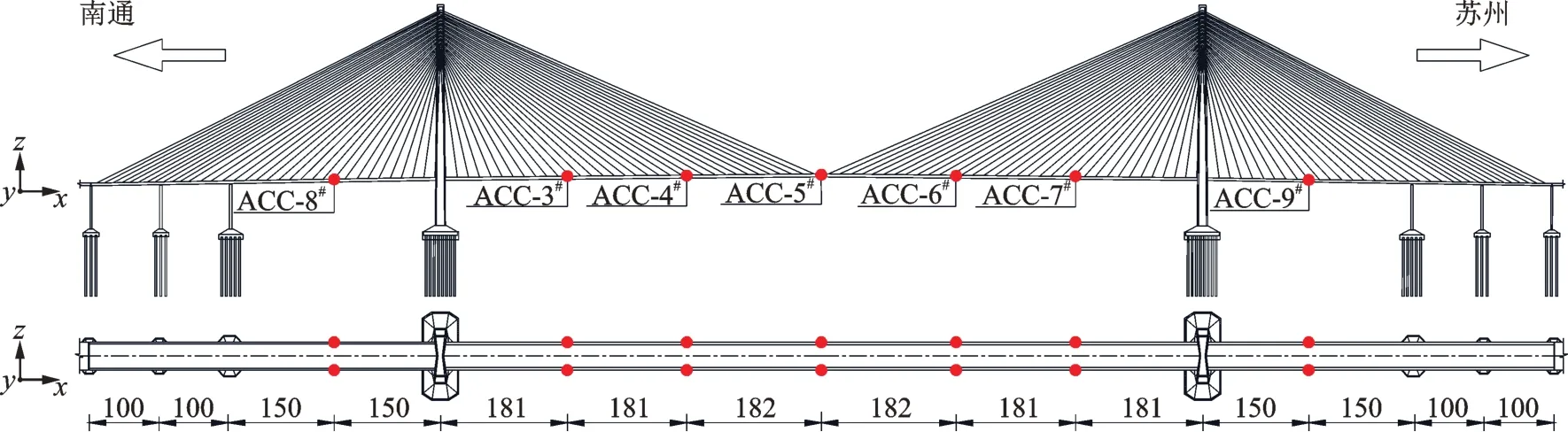
图5 苏通大桥主梁加速度传感器布置（单位：m）Fig.5 Layout of accelerometer on main beam of Sutong Bridge（Unit：m）

样本数据的PSD 谱与SV 谱如图6所示，其中，图6（a）中不同颜色曲线表示不同通道输出的加速度数据PSD，图6（b）中不同颜色曲线表示加速度数据PSD 矩阵的不同阶特征值，为节省篇幅，本节仅对该图中标记的4 阶竖弯模态进行识别。取频带宽度系数κ=10，苏通大桥的模态参数识别结果如表2与图7所示。由对应的结果可知，阻尼比与模态力功率谱密度不确定性较高，而频率与振型的不确定性相对较低。大跨度桥梁承受的车载、风载等激励在足够长的时间段内往往会表现出明显的非平稳性，无法满足高斯白噪声假设［20］。此外，桥梁结构阻尼比在不同的外部环境、荷载条件下存在显著的变异性，难以准确识别［21］。可能正是上述原因导致了模态力功率谱和阻尼比的不确定性偏大。

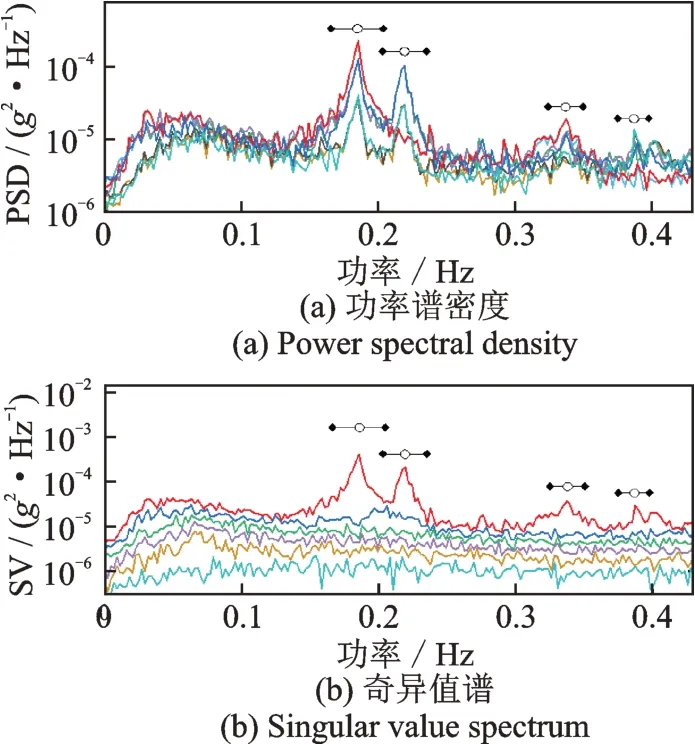
图6 样本数据功率谱密度与奇异值谱Fig.6 Power spectral density and singular value spectrum

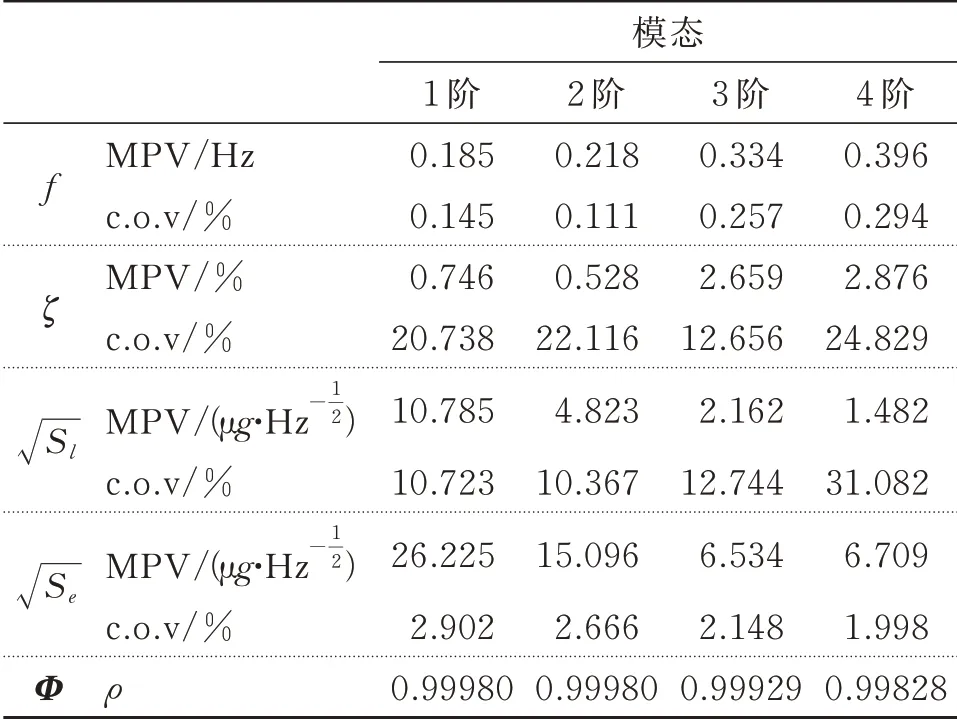
表2 模态参数识别结果Tab.2 Identified modal parameters

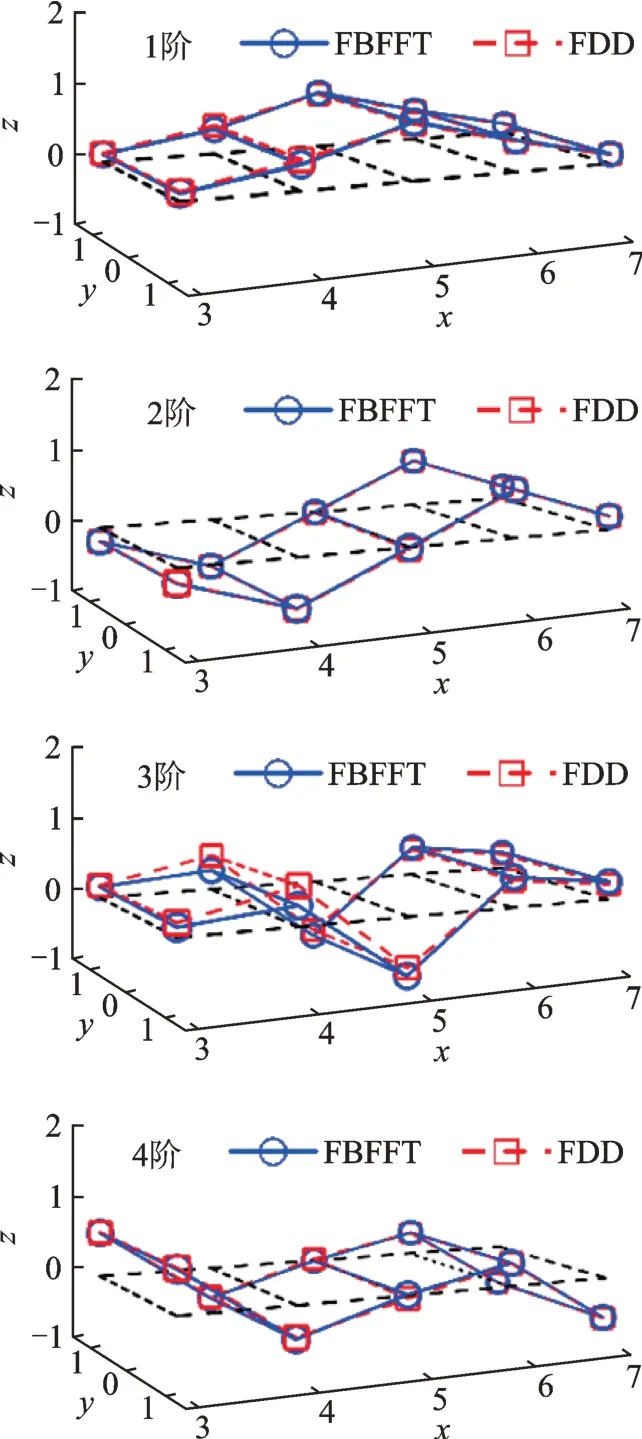
图7 振型识别结果Fig.7 Identified mode shapes

频率与阻尼比是桥梁结构重要的动力特性，也是模态参数识别中首要考虑的对象。因此，为分析频带宽度系数κ对模态参数识别结果的影响，本节计算了不同κ值对应的频率、阻尼比及其变异系数，如图8 和9所示。图中频率、阻尼比的参考值来源于文献［4］。由图8 和9 可知，随着κ的增大，识别结果与参考值的差异逐渐增大。第四阶频率与第三、四阶阻尼比受κ的影响最为明显，当κ大于12 后，识别值明显偏离参考值。总体上，c.o.v 随着κ的增大逐渐减小。但当κ增大到一定程度后，c.o.v 也可能表现出增大的趋势。上述结果表明，在一定范围内增大κ值有利于降低模态参数的不确定性，但当κ超过该范围后识别误差将逐渐增大，c.o.v 的变化也可能出现异常。

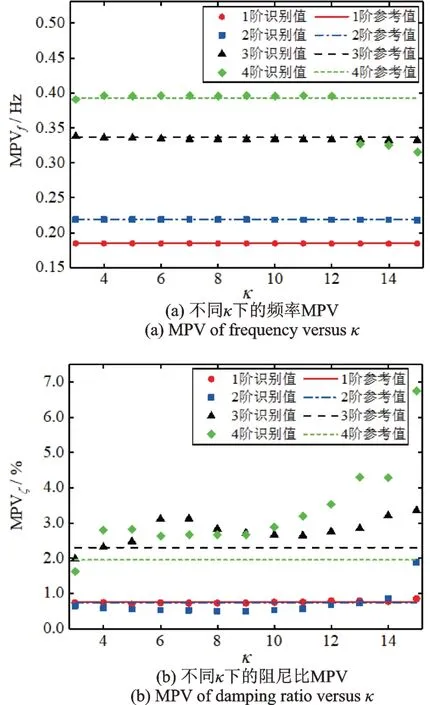
图8 模态参数MPV 随频带宽度系数的变化趋势Fig.8 Effect of bandwidth factor on MPV of modal parameters

图9 模态参数c.o.v 随频带宽度系数的变化趋势Fig.9 Effect of bandwidth factor on c.o.v of modal parameters

上述现象发生的原因主要包含两方面［22］：一方面随着κ的增大，样本数据量增大，样本能够提供更多的模态信息，有利于降低识别结果的不确定性；另一方面随着κ的增大样本中可能包含的其他模态信息也越多，模态分布越密集、频谱响应越微弱该现象就越突出（如第四阶模态），进而导致识别结果出现较大的误差。因此，在选择κ时应充分考虑频谱分布情况，并避免选择过大的κ值。从图8 和9看，κ在5 到10 之间时，既能确保模态参数的MPV具有较小的误差，又能让变异系数不至于过大且分布稳定［19］。

图10 展示了一阶模态各参数后验PDF 的分布情况，其中实线表示以各参数的MPV 为期望、Hessian 矩阵的逆矩阵为协方差矩阵拟合的高斯PDF，而虚线是式（7）所示的似然函数在各参数方向上的抽样。由图中可知，高斯PDF 与模态参数的概率分布吻合良好，表明在不确定性量化时利用高斯PDF代替参数的后验PDF 计算协方差矩阵是合理可行的［8］。

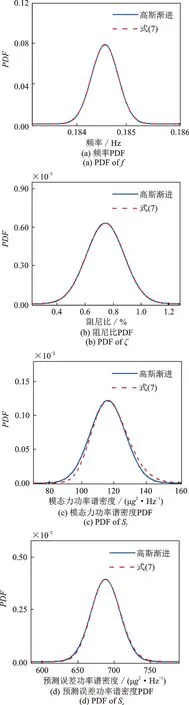
图10 模态参数后验概率密度函数Fig.10 Posterior PDF of modal parameters

4 结论

（1）将FBFFT 法与遗传算法结合，并利用渐进估计区间约束参数搜索范围，能够高效准确地识别大跨度斜拉桥的各阶模态参数。

（2）模态参数识别结果中，阻尼比与模态力功率谱密度表现出较大的不确定性，而频率与振型的不确定性相对较小。

（3）选择频带宽度系数时应适当考虑频谱分布特征，并将其限制在5 与10 之间以确保识别误差与不确定性的平衡。

（4）通过似然函数抽样建立的模态参数后验PDF 与高斯渐进结果高度吻合，符合模态参数的后验PDF 可用高斯PDF 代替的假设。