海上漂浮式激光雷达运动平台模拟器设计及应用❋

张凯临， 张文静， 秦胜光

(1. 中国海洋大学信息科学与工程学院， 山东 青岛 266100； 2. 青岛镭测创芯科技有限公司， 山东 青岛 266100)

测风激光雷达作为测量海面风场的一种重要设备，在工作时承载平台会受到海浪的作用，所以需要雷达的姿态修正算法参与风速风向的计算。为了模拟测风激光雷达的海上工作环境，验证海上漂浮式测风激光雷达的算法精度及工作稳定性，本文设计并实现了六自由度平台模拟海上浮动平台的运动。相比于出海进行实验和验证，将激光雷达先行安装于六自由度并联平台上进行测试，能够降低测风激光雷达在海上实验和工作所带来的人力、物力和时间成本，能够先行测试海上工作设备的工作能力。

从Gough和Stewart研制出并联平台机构起，对于六自由度平台的研究逐渐受到重视。如今，Stewart平台在飞行模拟器[1]、工业、机床和医用等领域广泛应用[2]，六自由度平台定位系统的精度[3-4]和隔振性能[5-7]也通过多种方式逐渐提高,随着航海事业、仿真技术和并联机构的发展，以并联机构为载体的多自由度运动模拟装置已广泛应用于船舶模拟方面研究。目前，多所高校和船舶公司已经设计出精度较高的船舶模拟装置[8-9]和潜艇模拟装置[10]。

21世纪初，通过对采集的风场数据进行姿态和速度矫正的方式来隔离平台运动对测风结果的影响[11]，现今海上测风激光雷达能够实时姿态矫正测量海上风场。本文中使用运动平台模拟器搭载海上测风激光雷达，对激光雷达进行不同输入数据下的测风实验，并使用地基测风激光雷达进行同步对比测风实验，研究平台运动对风场反演的影响。结果表明，平台的运动速度对风场的反演有影响，运动速度越快，反演误差越大。实验结果可为测风激光雷达反演算法的优化提供参考。

1 系统

1.1 机械结构

本文运动模拟器在Stewart结构的基础上增加了一个重力平衡气缸，平台整体结构由上下2个平台、6个电动缸、1个气缸、2个球头杆端关节轴承、2个Y型接头、6个组合轴承、若干十字轴承、万向节叉、轴用挡圈和孔用挡圈组成，图1为该六自由度平台结构三维模型。根据组合轴承和十字轴承的转动副、电动缸的移动副计算可得，该平台的自由度数为六，所设计的平台可实现上平台的六自由度运动。

上下平台以及轴承支撑架采用铝合金材料，强度高、重量轻，能够承载激光雷达系统。下平台和电动缸之间采用组合轴承和十字轴承共同连接的方式，能够让电动缸倾斜较大的角度，使得上平台绕X轴或Y轴的转动范围可达30°。

平台上搭载的激光雷达系统重量约为32 kg，为了六自由度平台能够在此负载下正常运动，该平台系统增加了平衡重力用的气缸结构。图2所示为带气缸的整体机械结构图，该气缸通过改变气压，能够平衡20～48 kg的负载的重力，满足海上激光雷达系统的各种运动要求。

图1 六自由度平台三维模型Fig.1 Three-dimensional model of 6-DOF platform

图2 六自由度平台实物图

运行过程中气缸随着平台运动，球头杆端关节轴承亦随之转动。气缸系统在运动过程中起着被动的平衡重力的作用，两端的万向节对平台运动位姿没有影响。设计的六自由度平台的工作空间如表1所示。

1.2 控制系统及数据源

控制系统采用工控机和运动控制卡[12]等控制电动缸的伸缩运动，运用气泵和恒压阀控制气缸的支撑力。电动方式驱动的平台整体体积小、响应速度快、精度高，但是承重较小[13]；气动方式驱动的平台承重相对较高，但是精度较低[14]；采用电气混合的控制方式能结合二者的优点，精度较高、响应快速的同时能承载较高的载重。

表1 六自由度平台工作空间

计算机通过运动控制卡和驱动器控制步进电机的转动，从而精密控制电动缸伸缩杆上下运动，十字轴承和组合轴承随着电动缸的运动转换任意角度，能够使上平台模拟漂浮平台的横荡、纵荡、垂荡、横摇、纵摇和艏摇六个自由度的运动。

在模拟实际海上浮动平台的运动过程中，最重要的是模拟浮动平台的横摇和纵摇运动。六自由度平台以青岛海域2020年5月21日的部分浮标实测数据为运动依据，录制了此段时间内的横摇角和纵摇角，作为模拟平台控制系统的输入数据。浮标运动数据之间间隔约为200 ms，其时间间隔相对较大，使得六自由度平台运动过程不够连贯，因此需要对浮标数据进行数据插值，选定插值时间间隔为10 ms。

图3表示浮标数据插值后的横摇波形和纵摇波形。图中纵坐标为角度，红色线代表横摇角度，蓝色线代表纵摇角度。此外，还增加一种固定频率的运动方式，对控制系统输入周期为2，幅度为分别为3°和6°的正弦运动数据作为六自由度平台横摇、纵摇和艏摇单自由度运动的输入数据。图4是周期为2、角度偏移幅度为3°的正弦运动波形。

图3 浮标运动波形Fig.3 Buoy motion waveform

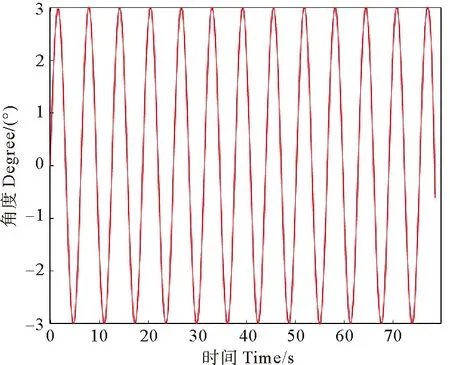
图4 正弦运动波形

为研究运动频率和幅度对风场反演的影响，平台在上述输入数据基础上分别对频率和幅度进行了缩放。将浮标数据的频率减少一半，与原有浮标数据对比研究频率对风场反演的影响；将正弦数据的幅度增加一倍，与原有正弦数据对比研究幅度对风场反演的影响。

六自由度平台系统依据上述输入的多种运动数据，经过下文中介绍的坐标变换，求得每组数据的电动缸位移量，经由软件程序及运动控制卡等控制六自由度平台模拟受海浪影响的浮动平台的运动。使用外部的角度测量传感器测得该平台在模拟输入数据运动时，空载误差范围在0.2°以内，其精度较高，能够良好地模拟海上浮动平台的运动，为激光雷达的测试提供准确的漂浮平台工作环境。

1.3 激光雷达系统

激光雷达系统采用了镭测创芯的脉冲相干测风激光雷达WindMast 350-M，可以在条件恶劣的海洋环境中使用。系统采用多波束/VAD扫描方式是一种传统且常用的技术[15]，激光雷达系统自带反演算法和姿态校正算法实时反演风速和修正精度，最终得到东北、东南、西南、西北和垂直五方向的风场数据。表2为该激光雷达的具体参数：

表2 测风激光雷达参数(10 min数据产品精度)Table 2 Wind measurement lidar parameters (10 min data product accuracy)

2 运动学分析

在图5(a)和5(b)中分别建立了上下两个坐标系，一个位于下平台上方铰链的定坐标系x,y,z,该坐标原点o位于下平台铰链点组成圆的圆心；一个位于上平台下方铰链的动坐标系x′,y′,z′，该坐标原点o′位于上平台铰链点组成圆的圆心。在初始位置时，上下两个坐标系x,y,z三轴方向均一致，且z轴在同一条直线上。沿z轴进行投影，得到上下平台的铰链点分布图。

图5(a)为固定坐标系下的各个铰链点分布示意图，下平台两点之间的角度为ω，铰链点组成圆的圆半径为Rb。图5(b)为动坐标系下的各个铰链点分布示意图，上平台与下平台之间相差60°，上平台两点之间的角度为φ，铰链点组成圆的圆半径为Ra，上下平台各铰链点的坐标可根据角度和半径求得。

图5(a) 下平台铰链点分布图Fig.5(a) Distribution of lower platform hinge points

本文中六自由度平台依照浮标运动数据来进行运动，表示为已知动平台的运动反解求六个电动缸的运动。动平台在空间中的位姿(x,y,z,α,β,γ)[16-17]为参考点(动平台中心)相对于中位时的位置(x,y,z)及姿态角(α,β,γ)。

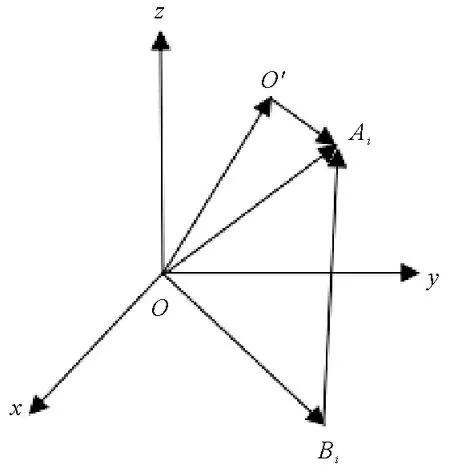
图6 空间关系矢量图

图6为空间关系矢量图。其中：O为静坐标系原点；O′为动坐标系原点；Os′为O′在静坐标系中的坐标。动静平台在设计时已确定尺寸，动静平台各铰链点的坐标亦随之确定。动坐标系任意一点都可经过坐标变换变换到静坐标系。围绕x轴旋转α角度后，变换矩阵为Tx，围绕y轴旋转β角度后，变换矩阵为Ty，围绕z轴旋转γ角度后，变换矩阵为Tz。

(1)

T为坐标变换矩阵:

(2)

动平台任意一点Ai转换到静坐标系的坐标值为Ai′：

Ai′=TAi+Os′。

(3)

六根驱动杆杆长的矢量为：

Li=Bi-(TAi+Os′)。

(4)

由图可得，电动缸长度li为动平台铰链点Pi′和对应静平台铰链点Mi之间的距离。li为：

(5)

电动缸的伸缩量Lei为：

Lei=|li|-|li|init。

(6)

其中:|li|init为电动缸的初始长度,上述i=0,1,…,5。依据浮标数据提供的位置姿态以及上述公式反解出六根驱动杆的伸缩量。在控制系统中编写计算所得的驱动杆伸缩量程序，可以控制六自由度平台根据浮标数据运动。

3 实验数据及分析

两台测风激光雷达WindMast 350-M于2021年1月29日进行对比实验(见图7)。两台激光雷达实验时平行放置，其中一台安装惯导的激光雷达固定于六自由度平台上，随着六自由度平台的运动进行测量。另一台测风激光雷达静置于地面进行同步对比实验[18]。激光雷达的运动数据包括浮标的运动数据、频率缩小一半的浮标运动数据、幅度为3°的正弦数据和幅度为6°的正弦数据。获得的测风激光雷达数据包含了GPS数据、信噪比数据和20～350 m不同高度上秒级的实测风速和风向等数据。

图7 现场实验图

本文风速风向数据皆选自高空50 m处的风场数据。图8(a)和8(b)为两台激光雷达均静止时，一段时间内的风速和风向的对比图。本节图中蓝色线均为地基测风激光雷达测得的风场数据，红色线均为运动平台上测风激光雷达测得的风场数据。

图8(a) 静止时风速对比图Fig.8(a) Wind speed comparison at rest

由图8可知，该段时间的风速大多在3～9 m/s之间，且风速随着时间变化较快；风向基本在140°～220°之间变化，该段时间的风主要为西南风。对该段时间的风速误差和风向误差进行了平均，其中，风速平均误差为0.019 8 m/s,风向平均误差为2.021 9°，误差较小且均在测风激光雷达误差范围内。说明两台测风激光雷达在静止时反演的风速和风向基本一致，拟合较好，同时为下文六自由度平台模拟不同运动时测得的风场数据提供对比依据和基准。

平台输入浮标数据为青岛海域2020年5月21日部分浮标实测姿态数据，对输入数据进行了10 ms的插值处理后，得到了53 946个姿态数据。图9(a)和9(b)分别表示运动平台输入浮标数据时风速和风向对比图。

图9(a) 输入浮标数据风速对比图 Fig.9(a) Input buoy data wind speed comparison chart

由图9可知，该段时间内风速大多在3～7.5 m/s之间变化，风向大多在120°～200°之间变化。与平台静止时间段相比，风速有所减小，同为西南风。该运动状态下测得的平均风速误差为0.148 4 m/s,平均风向误差为3.534 3°。其中，单台测风激光雷达的风速精度≤0.1 m/s，风向精度<3°，实验为两台测风激光雷达的数据对比，平台输入浮标数据时的平均误差在两台测风激光雷达的误差范围内。该运动状态下测得的平均误差均比平台静止时的平均误差大，说明平台的运动对风场反演有影响。

将上述幅度相同，频率缩小一半的浮标数据输入到运动模拟器中。图10(a)和10(b)分别是平台测风激光雷达在这种运动下测得的风速和风向，与同一时间内地基测风激光雷达测得的风速和风向的对比图像。

由图10可知，该段时间风速基本在1～5 m/s之间变化，风向基本在100°～180°之间变化。图10(a)中，两台测风激光雷达的平均风速误差为0.074 3 m/s,图10(b)中，平均风向误差为2.228 8°。数据显示，运动平台输入频率缩小一半的实测数据时，其风速和风向的平均误差较小。说明平台运动频率对风场的反演有影响，且平台运动的频率越快，误差也就越大。

图10(a) 输入半倍频浮标数据风速对比图

对平台的横摇、纵摇和艏摇3个自由度分别输入周期为2π、幅度为3°和6°的正弦姿态数据，研究平台运动幅度对反演风场的影响。图11(a)和11(b)分别表示平台在输入运动幅度为3°的正弦数据时，测风激光雷达测得的风速风向与地基测风激光雷达测得的风速风向对比图。

图11(a) 平台运动幅度为3°时风速对比图

由图11可知，平台在该运动状态下测得的平均风速误差为0.026 3 m/s,平均风向误差为2.020 9°。此外，对运动模拟器输入了幅度为6°的正弦数据，图12(a)和12(b)分别表示两台测风激光雷达在该数据运行时测得的风速和风向对比图。

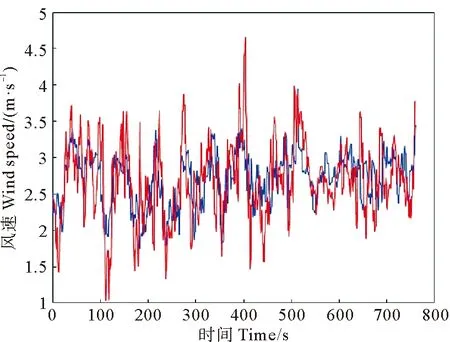
图12(a) 平台运动幅度为6°时风速对比图

图12测得此时的平均风速误差为-0.022 1 m/s,平均风向误差为2.656 9°。总结上述五种情况下的平均风速误差和平均风向误差，如表3所示。

表3 平均误差总结

综合上述五种情况的误差总结，平台静止时的平均风速误差最小，为0.019 8 m/s；平台静止时的平均风向误差与最小的平均风向误差基本相同，为2.021 9°，表明平台静止时测得的风速风向误差最小，拟合最好。说明平台的运动对风场的反演有影响。

平台输入浮标数据和频率缩小一半的浮标数据时，不管是从绝对误差来看，还是从二者与平台静止时的相对误差来看，平台运动频率缩小时测得的平均误差更小。平台输入周期为2π、幅度分别为3°和6°的正弦数据时，两种输入数据测得的平均风速误差和平均风向误差相对接近。平台输入幅度为3°的正弦数据时，测得的平均风速误差的数值大，为0.026 3 m/s；输入幅度为6°的正弦数据时，平均风向误差的数值大，为2.656 9°，这难以说明平台运动幅度对风场反演的影响。但是，以平台静止时的平均误差为基准，平台输入幅度为3°的正弦数据时，平均风速相对误差是0.006 5 m/s，平均风向相对误差是-0.001°。平台运动幅度为6°时，平均风速相对误差是-0.041 9 m/s，平均风向相对误差是0.635°。说明了平台运动幅度对风场的反演有影响，平均误差随着幅度的增加而增加。

平台运动频率和运动幅度对风场反演的影响都可以归结为平台运动的速度对风场反演的影响。运动频率和幅度增大时，其速度都相应增大。表明平台运动的速度越快，其平均误差也就越大。反演风场数据时需要考虑到平台运动速度对反演的影响。

4 结语

本文介绍的海上漂浮式激光雷达运动平台模拟器能够模拟海上浮动平台的运动，且能够搭载海上测风激光雷达进行测风实验，可有效降低外场实验成本。对比平台静止和平台不同运动模式时，运动时测得的平均误差比静止时测得的平均误差大，表明平台的运动对风场反演有影响，风速和风向的平均误差随着平台运动速度的增加而增加。实验证明，运动模拟器可广泛应用于验证海上实验设备的工作性能，为海上测风激光雷达反演算法的改进和优化提供参考。