基于蒙特卡罗效率刻度方法的海洋原位放射性监测技术研究❋

任国兴， 厉运周， 张颖颖， 刘东彦

(1.中国海洋大学信息科学与工程学部， 山东 青岛 266100； 2. 齐鲁工业大学(山东省科学院)海洋仪器仪表研究所， 山东 青岛 266100)

自日本福岛核电站事故以来，海水的放射性污染成为海洋环境监测关注的热点。传统的监测手段每年进行1～2次重点海域站位取样、实验室处理，然后再进行分析，其周期较长，不能对一些突发事故引起的放射性污染进行及时监测和有效预警。海水放射性原位监测技术具有实时、在线的特点[1]，对其开展研究具有重要意义。

在对海水的放射性污染监测技术中，γ谱法应用最广泛[2]。γ谱法的原理如下：海水中放射性核素在衰变过程中会发射出不同能量的γ射线，γ射线与闪烁晶体相互作用后产生荧光，荧光被光电器件获取后以脉冲电信号的形式输出处理，将脉冲信号的计数量对应为不同能量描绘的γ能谱，通过分析能谱，计算出核素的活度。

放射性测量仪器的探测效率是定量分析γ能谱的一个重要物理量，它表征了γ射线照射量率与探测器输出脉冲计数之间的关系。在监测仪器布放之前必须要进行效率的刻度校准，刻度校准的优劣直接影响测量结果的准确性[3-4]。

传统的方法是利用多个γ标准放射源在实验室对仪器进行效率刻度。传统刻度方法不可避免地会对实验人员造成一定的辐射[5]，且放射源管理严苛、不能轻易获得满足要求的数量。而对海水的放射性测量而言，能溶解于海水中的单能γ射线核素的数量相当有限，很难建造一个足够大的水箱来模拟真正的海洋环境，含有人工核素的试验废水难以处理。以上问题使得在实验室进行效率刻度变得非常困难。

蒙特卡罗方法是一种随机实验方法[6]，其基本原理是利用大量随机实验的平均结果来近似求解问题的解。蒙特卡罗方法与所求解的问题维数无关，收敛速度可以预测，能够准确地描述粒子传输的物理过程，在复杂放射性测量分析方面具有独特优势，因此在核物理研究中得到广泛应用[7]，已成为研究人员设计、分析和测试放射性测量仪器的重要手段。已有的研究大多数是为了研究陆地上某些位置的不同放射源的响应特性和效率校准方法，或者研究具有不同形状、体积和材料的仪器设备的响应特性和效率校准方法[8-9]。近年来，随着海洋放射性监测技术的发展，已经出现蒙特卡罗方法在海洋放射性监测方面的模拟，主要模拟计算探测器在海水中的本底能谱图,以增加能谱分析的置信度[10-11]。

本文针对海洋原位放射性监测技术中使用的NaI(Tl)晶体探测器，采用蒙特卡罗的MNCP程序对NaI(Tl)晶体探测器和海水环境进行模拟，研究海洋环境中多种放射性核素的探测效率校准，拟合了γ射线的探测效率与能量关系的曲线，并在此基础上研制了海洋原位放射性监测仪。在青岛海域进行了海洋原位放射性监测仪的海上实验，使用海水中天然存在的K元素进行了探测效率的计算。

1 仿真及数学计算

1.1 建立蒙特卡罗模型

使用MNCP程序模拟全能峰探测效率分为如下几步：

(1)建立NaI(Tl)探测器物理模型。模型参数如下：探测器的尺寸、结构，各部分材料的成分、密度，海水的密度等。

(2)描述探测器在海水中的位置。

(3)用MNCP程序表达上述模型。

(4)模拟计算，并对模拟结果进行处理。

根据以上论述，结合NaI(Tl)探测器的结构、尺寸，建立了仿真模型。探测器由75 mm × 75 mm的NaI(Tl)晶体和光电倍增管(HAMAMATSU CR109)组成，它们与集成电路一起封装在铝材质的水密圆柱形外壳中。采用MNCP程序，对装在半径分别为10、20、…、120 cm的球形水箱中的放射源和海水(密度为1.025 g·cm-3)进行了放射性探测效率的模拟，忽略光电倍增管、电路和电缆，将探测器简化为闪烁晶体，置于模拟装有海水的模型中心。为了更真实地模拟探测器在实际海水中的测量情况，在模型中考虑了由于晶体周围的铝外壳而引起的γ射线衰减。计算模型如图1所示。计算模式为P模式，模拟光子数为1×108个。

图1 海水中NaI(Tl)探测器仿真模型平面图Fig.1 Plane view simulation model of NaI(Tl) detector in seawater

1.2 探测效率模拟

对于陆地上的点源检测，探测效率定义为在一定的探测条件下，探测器测得的粒子数与在相同时间内由辐射源发射出的该种粒子数之比。与陆地点源探测不同，海洋放射性测量是一种体源探测，在探测效率上有不同的模拟计算方法[12]。在海水中，具有不同活度的某种放射性核素，单位时间的全能峰计数不同，即全能峰计数率(单位为 cps)不同。用相对全能峰计数率，即单位活度的全能峰计数率来描述海洋探测效率[13]，单位为 cps/(Bq·m-3)。

海水中不同的核素在发生衰减时会产生与其核素衰减能量相同能量的γ射线，不同能量的γ射线有着不同的吸收率，海洋中放射性核素的探测效率与探测半径、γ射线能量有关。图2给出了用MCNP程序模拟的能量分别为511、662、835和1 460 keV的γ射线在海水中不同距离的探测效率曲线。由图2可以看出，海水中探测半径越大，探测效率就越高。当探测半径足够大时，探测效率达到饱和值[14-15]。

图2 海水中不同γ射线能量的距离-探测效率曲线Fig.2 Distance-detection efficiency curves of different γenergies in seawater

为使效率刻度更精确，在实际工作中可用相同方法模拟更多的γ射线能量的距离-探测效率曲线。当曲线达到饱和值后，将这些饱和值进行平均，便可得到对应的γ射线能量的探测效率(见图3)。

图3 能量-探测效率曲线

根据图3能量-探测效率曲线可得到NaI(Tl)探测器的能量与探测效率εs的关系式：

(1)

式中：E是γ射线的能量；a、b、c和d是拟合参数。

2 系统实现

2.1 海洋放射性原位测量仪原理

海洋放射性原位测量仪硬件系统由NaI(Tl)晶体探测模块、数字化多通道脉冲幅度分析模块、电源模块、通信模块和封装外壳组成(见图4)。晶体探测器模块主要由75 mm国产NaI(Tl)晶体(662keV的能量分辨率小于7%)、低钾光电倍增管和前置放大电路组成，使用光耦合材料优化光电转换效率。电源模块提供光电倍增管工作需要的高压和其他电子器件的工作电压。测量仪采用标准串口输出数据，上位机的能谱处理解析软件具备自动执行数据接收、存储、解析、显示及设置等功能。

图4 测量仪主要构成Fig.4 Sensor main composition diagram

海水中的γ射线照射在NaI(Tl)闪烁晶体上发出荧光，晶体探测器模块收集荧光，然后将荧光信号处理成与检测的γ射线能量成正比的脉冲电压。微弱的脉冲电压信号通过放大、整形后进行脉冲幅度分析，计数得到γ能谱。测量仪将能谱数据传输给上位机软件，上位机软件自动解析甄别。

2.2 海洋放射性原位测量仪封装

测量仪的封装结构如图5所示，NaI(Tl)晶体探测模块采用铝外壳封装，内部采用光耦合材料优化探测器的光电转换效率。综合考虑防水、耐压、耐腐蚀、对γ 射线衰减的影响及制作工艺，本研究选择尼龙作为测量仪的整体封装外壳材料。测量仪实物组装完成图如图6所示。

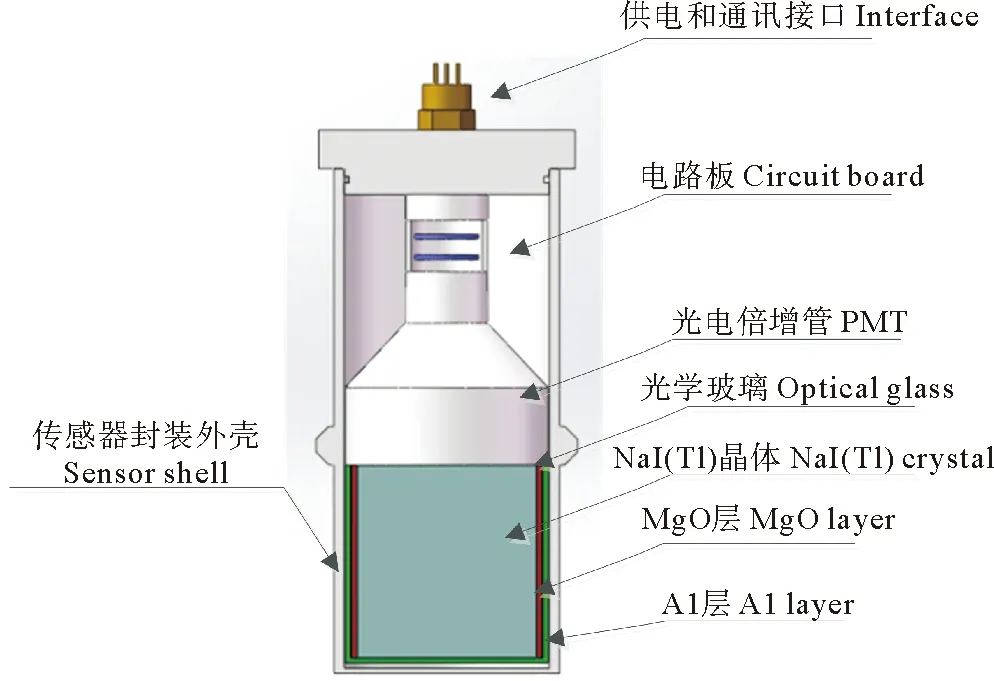
图5 测量仪封装结构图

图6 测量仪组装图Fig.6 Sensor assembly diagram

3 海上实验

进行海上现场实验之前，在实验室用137Cs、60Co、40K和54Mn四个参考放射源对NaI(Tl)晶体探测器进行了能量校准。完成实验室能量校准后，在青岛八大关码头进行了测量仪的海上现场实验。实验现场的水深为8 m左右。如图7所示，使用吊车将测量仪悬挂于水面下3 m处，以减少海底和宇宙辐射对测量的干扰。使用笔记本电脑进行实时测量和数据采集，使用采集到的能谱数据进行放射性核素的定性和定量计算。

图7 海上实验

图8是海上实验24 h连续测量得到的能谱曲线，从图8可以看到，在1 460 keV能量处出现用来比对模拟效率和实测效率所需的40K特征峰。

图8 海洋现场实验24 h能谱

在海上实验中，海水的盐度为30.98。海水中钾的含量约为1.1%、40K在钾中约占11.7‰，海水中40K的活度为1.897×10-2Bq·m-3，由上述关系，根据公式(2)[16]可计算40K的探测效率ε：

(2)

式中：N为全能峰计数，可通过图8扣除本底后解谱得出；c为活度(Bq·m-3)；I为γ光子发射率，与核素相对应，是常数；t为测量时间。通过公式(2)计算可得，现场实验得到的40K的探测效率为1.68×10-4cps/(Bq·m-3)，根据公式(3)[17]计算模拟效率与实测效率的相对偏差：

(3)

式中：E为模拟效率与实测效率的相对偏差；Ds为模拟效率；De为实测效率。将模拟效率Ds=1.70×10-4cps/(Bq·m-3)、实测效率De=1.68×10-4cps/(Bq·m-3)代入公式(3)中，可得二者的相对偏差E=1.19%，由此可见，本研究的实验结果与模拟结果具有很好的一致性。

4 结语

探测效率是在海水中工作的放射性原位测量仪的重要性能指标之一，也是定量计算海水中放射性核素的重要参数。由于海洋环境的复杂性，海洋的放射性探测与当前成熟的陆地放射性探测有很大的差异。鉴于实验室刻度和定量测试的困难，本文利用蒙特卡罗方法对自行研发的NaI(Tl)探测器的效率刻度进行了模拟和分析，得出了适合海水放射性原位监测仪器的效率拟合曲线。将基于NaI(Tl)探测器的海水放射性原位测量仪进行了海上实验，用实测的40K倒推出的探测效率值与用蒙特卡罗方法模拟计算得到的探测效率值非常接近，这证明了本研究的可行性。

下一步将对海洋原位放射性测量的蒙特卡罗模拟开展持续的研究，进一步利用蒙特卡罗方法模拟核泄漏时放射性核素的海洋探测效率数据，为核事故应急提供理论依据。