调和Hardy空间上调和Toeplitz算子的若干代数性质❋
魏晓东, 石岩月
(中国海洋大学数学科学学院, 山东 青岛 266100)
在Hardy空间上,一个有界线性算子A是Toeplitz算子当且仅当UAU*=A,其中U和U*为H2上的单侧移位算子。1964年由A. Brown, P. Halmos[1]给出该方程,利用Toeplitz算子满足该方程的特性,证得了一系列有关经典Hardy空间上Toeplitz算子的重要的代数性质。一般地,将该方程称为Hardy空间上Toeplitz算子的特征方程。在不同函数空间上探究各种算子的特征方程是函数空间上算子理论研究的重要课题之一。2007年D. Sarason[2]首先在模型空间上给出了截断Toeplitz算子的定义,并给出了此类算子的特征方程。随后,国内外很多学者对截断Toeplitz算子进行了一系列深入的研究[3-10]。鉴于对偶截断Toeplitz算子和截断Toeplitz算子成对出现且具有紧密联系,丁宣浩和桑元琦[11]最先对两个对偶截断Toeplitz算子的乘积展开研究,分别给出了乘积为零、乘积为有限秩算子以及乘积为对偶截断Toeplitz算子的充要条件。随后,丁宣浩、桑元琦和秦越石合作对此类算子生成的C*代数进行了研究[12];丁宣浩、桑元琦和李永宁合作刻画了以函数φ(z)=z为符号的对偶截断Toeplitz算子的换位及其不变子空间[13]。最近,顾才兴[14]给出了对偶截断Toeplitz算子的特征方程,结合此特征方程和复对称性给出对偶截断Toeplitz算子的判定方法,并利用该方程部分简化了文献[11-12]中的证明。2020年,丁宣浩、秦越石和桑元琦[15]给出了调和Hardy空间上的调和Toeplitz算子的定义,并研究了算子的有界性和紧性问题、零积问题、乘法封闭性和交换性问题。目前对调和Hardy空间上调和Toeplitz算子的研究还相对较少。本文主要从算子方程的角度进行研究,将顾才兴[14]给出的对偶截断Toeplitz算子的若干性质推广到调和Toeplitz算子。
1 预备知识
记复平面上的开单位圆盘为
D={z∈C:|z|<1}。
设L2为单位圆周上关于弧长测度平方可积的可测函数全体构成的空间,设H2为L2中负项傅里叶系数为零的函数全体构成的空间,即


在上述结论的启发下,丁宣浩、秦越石和桑元琦[15]给出了调和Hardy空间的定义。在本文中均设u,v为Hardy空间的内函数,由u,v诱导的调和Hardy空间定义如下:
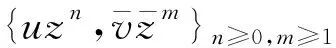
Mu(f)=uf;Mv(f)=vf;
设



事实上,∀g∈L2,





又由于Quv是自伴算子,所以
从而

在本节的最后,我们回顾一下复对称算子的定义和相关研究成果。令H为可分的无穷维复Hilbert空间,L(H)是H上的有界线性算子全体构成的赋范线性空间。令C为Hilbert空间上的算子,且C满足:

(Ⅱ)〈Cx,Cy〉=〈y,x〉,∀x,y∈H;
(Ⅲ)C2=I,其中I为单位算子。
由性质(Ⅱ)知C为H上的等距算子。一般地,称满足上述三个条件的算子C为H上的对合的共轭线性等距算子。
设T∈L(H),若存在对合的共轭线性等距算子C:H→H使得
T=CT*C,
则称T为关于算子C的复对称算子。
复对称算子最早是由S. Garcia和M. Putinar[17]从复对称矩阵推广到Hilbert空间的。郭坤宇和朱森[18]最先提出了Hardy空间上Toeplitz算子的复对称性问题。由于对合的共轭线性等距算子C选取的多样性,要完全回答该问题是非常困难的。目前关于该问题的研究主要有两个思路:一个是先构造特定的对合共轭线性等距算子C,然后研究Toeplitz算子对指定算子C的复对称性[19-20];另一个是适当限制Toeplitz算子的符号函数,根据复对称算子的性质寻找符号函数必须满足的条件[21]。关于Bergman空间和Dirichlet空间上的Toeplitz算子的复对称性问题的研究可参见文献[22-24]及其参考文献。

2 主要结果及其证明
在本节中,我们将建立调和Toeplitz算子满足的一些算子等式;然后构造适当的对合的共轭线性等距算子C,证明调和Toeplitz算子关于C均是复对称的。


其中u0=u(0),v0=v(0)。

(1)
其中,第三个等号是因为
注意到

将此式代入等式(1)中,
其中,第三个等号是因为
注意到
〈h,u〉=〈uf,u〉=f0。
从而
故结论得证。

其中u0=u(0),v0=v(0)。
证明 由于等式(Ⅰ)和等式(Ⅱ)的证明类似,我们只给出(Ⅰ)的详细证明过程。首先利用引理3中(Ⅰ)可得
(2)
从而
(3)
利用引理3(Ⅱ)可得
所以
(4)
(5)
(a) 验证当h=uzn时,等式(Ⅱ)成立。
当n=0时,
当n≥1时,
另一方面,


利用等式(4)和等式(5)可得
通过1秩算子u⊗u的定义可得
所以
即结论(Ⅰ)成立。
定理5对任意φ∈L∞,设
下面等式成立
(6)

容易验证

(7)

(8)
将上述等式分别代入等式(6)可得
再根据引理3(Ⅱ),
注意到


由此


其中γ如条件中所设。进而

由于Quvh=h,可以证明
因此
(9)
利用等式(9)可得
结论得证。
上述定理表明,对任意整数n≥0,m≥1,下列等式成立,
也就是说,
具有分块矩阵表示为

上式中:A和D为无穷维Toeplitz矩阵,B和C为无穷维Hankel矩阵。设T=(ti,j)i,j≥1。若ti,j=ti+1,j+1,则称T为一个Toeplitz矩阵;若ti,j+1=ti+1,j,则称T为一个Hankel矩阵。


设n为非负整数,b为复数,则
于是
记
则





证明 利用h的展开式可得
进一步计算可得
从而

定理7设φ∈L∞,则

(10)

(11)
(12)

于是
结合等式(10),等式(11)和等式(12)可得:
另一方面,再次利用引理3(Ⅰ)可得
由于

利用引理6,可以验证
于是
另一方面,通过计算可得



其中
结合等式(7)和(8)可以验证

接下来,验证


Cuv(aφ)=αu,

等价于对任意n≥1,均有
从而结论得证。

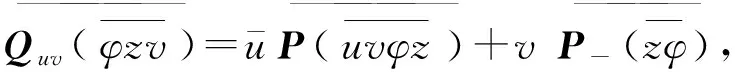
由此得出



另一方面,