两种分裂点连接运算图的 Randi´c 谱∗
卢志琴,马小玲
(新疆大学数学与系统科学学院,新疆乌鲁木齐 830017)
0 引言
本文考虑的所有图均为简单且无向的图. 设G=(V(G),E(G))是一个图, 顶点集为V(G)={v1,v2, ···,vn},边集为E(G). 图G的邻接矩阵记为A(G) = (aij)n×n, 如果vi和vj是邻接的, 则aij= 1; 否则, aij= 0. 设di=dG(vi)是G中点vi的度, D(G)=diag(d1,d2,···,dn) 是对角矩阵. 1975 年, Randi´c提出了Randi´c指标, 定义为[1]
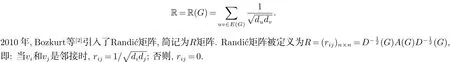
根据定义, 图G的规范化拉普拉斯矩阵和规范化无符号拉普拉斯矩阵分别定义为L(G)=In−D−1/2(G)A(G)D−1/2(G)和Q(G)=In+D−1/2(G)A(G)D−1/2(G), 其中In为n阶单位矩阵. 对于矩阵Mn×n, 我们用fM(x)表示M的特征多项式, 即fM(x)=det(xIn−M). 因此, fR(G)(x)(fL(G)(x), fQ(G)(x))是Randi´c矩阵(规范化拉普拉斯矩阵, 规范化无符号拉普拉斯矩阵)的特征多项式, 它的根是Randi´c矩阵(规范化拉普拉斯矩阵, 规范化无符号拉普拉斯矩阵)的特征值. 将R(G), L(G)和Q(G)的特征值分别表示为:
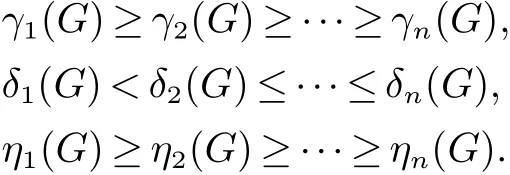
注意到δ1(G)=0. 显然, Randi´c矩阵与规范化拉普拉斯矩阵和规范化无符号拉普拉斯矩阵有直接的联系(见文献[3]): L(G)=In−R(G), Q(G)=In+R(G). 如果γi是R特征值, 则L的特征值δi和Q的特征值ηi分别可以表达为:

因此,同一个图G的L矩阵和Q矩阵的特征值可以被R矩阵的特征值所确定. R(G)(L(G), Q(G))矩阵的特征值及其重数的集合称为R-谱(L-谱,Q-谱). 两个图如果有相同的R-谱(L-谱, Q-谱), 则称其为R同谱(L同谱, Q同谱).
近年来, 一些学者研究了由图运算构造的图的谱性质. 在这个研究方向上有一些著名的图运算, 例如: 不交并、笛卡儿积、Kronocker积、强积、字典积、冠运算、边冠运算、邻接冠等. 这些图的谱结果见文献[4−9]. 两个图的连接运算[10]是它们的不交并, 将一个图的每个顶点连接到另一个图的每个顶点上, 并且保持两个图中的原有边. 一个图G的分裂图[11]记为SP(G), 是将G的每个点u做一个拷贝u′, 然后将u′与u的所有邻点相连而得到的图. 新增加的点集记为S(G), 即S(G)=V(SP(G))V(G). 现在我们基于分裂图, 给出以下两种类型的图运算.
定义1 设G1和G2是两个点不交的图, 点数分别为n1和n2. 则
(i) G1和G2的分裂V-点连接图, 记为G1⊻ G2, 是将SP(G1)中V(G1)的每个点与G2中的每个点连接而得到的图.
(ii) G1和G2的分裂S-点连接图, 记为G1⊼ G2, 是将SP(G1)中S(G1)的每个点与G2中的每个点连接而得到的图.
注意到如果Gi有ni个点和mi条边, i=1,2, 则G1⊻G2有2n1+n2个点和3m1+n1n2+m2条边,G1⊼G2有2n1+n2个点和3m1+n1n2+m2条边.
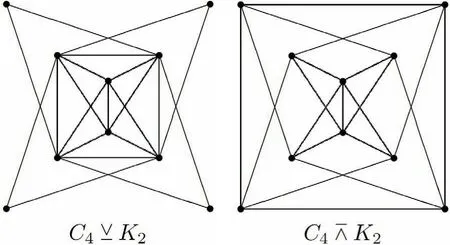
图 1 C4和K2的分裂V-点连接图和分裂S-点连接图
例 1 设G1和G2分别为圈C4和完全图K2. 两个图C4⊻K2和C4⊼K2如图1所示.
1 准备工作
对于任意整数k, n1和n2, Ik记为k阶单位矩阵,1k记为k阶全1列向量,Jn1×n2是所有项为1的n1×n2阶矩阵.
引理 1[12]设M1, M2, M3, M4分别为p×p, p×q, q×p, q×q矩阵且M1和M4是可逆的. 则
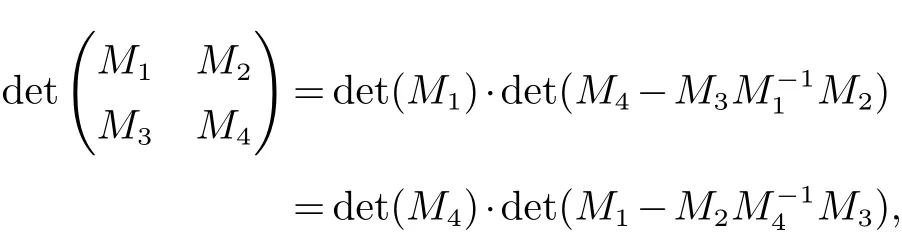
其中M1−M2M−14M3和M4−M3M−11M2分别称为M4和M1的Schur补.
引理2[4]设A是一个n×n阶实矩阵, Jn×n为n×n阶矩阵, 其所有元素都为1. 则
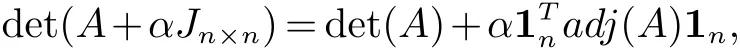
其中α是一个实数, adj(A)是A的伴随矩阵.
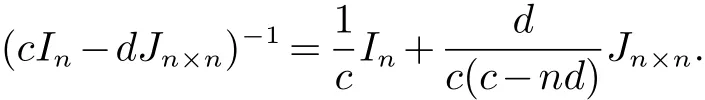
根据电网络理论, Klein和Randi´c[14]提出了一个名为电阻距离的距离函数. 给定图G中任意一对顶点vi和vj,设{i}表示vi和vj之间的电阻距离.
Chen和Zhang[15]证明了电阻距离可以自然地用规范化拉普拉斯矩阵的特征值和特征向量表示, 并引入了另一个图不变量, 定义为Kf∗(G)=i 引理 4 设G为n个点,m条边的连通图, {0=δ1<δ2≤···δn}是G的L(G)的谱, 则 (i)[15]G的度基尔霍夫指数为 引理3[13]对任意实数c,d>0, 我们有 (ii)[18]G的生成树数目τ(G)有下列式子 n×n矩阵M的M-冠[16−17]记为ΓM(x), 被定义为(xIn−M)−1矩阵的所有元素的和, 即: 引理5[19]如果M是一个n阶矩阵且行和等于常数t 在这一部分中, 我们得到了两个正则图的分裂V-点连接图的R-谱, L-谱, Q-谱以及相关谱的一些应用. 设Gi是ni个点的ri-正则图,i=1,2. 根据定义1(i),G1⊻G2的点可以由V(G1)∪S(G1)∪V(G2)构成,其中V(G1)={v1,v2,···,vn1}, S(G1)={v′1,v′2,···,v′n1}, V(G2)={u1,u2,···,un2}. 显然, G1⊻G2的点的度为: G1⊻G2的邻接矩阵和对角矩阵可按V(G1), S(G1)和V(G2)的顺序表示为如下块矩阵形式: 则G1⊻G2的Randi´c矩阵可表示为: 证明 G1⊻G2的Randi´c矩阵的特征多项式是 其中 则 因此, 定理1得证. 值得注意的是, 对于一个图G, 有L(G)=I −R(G), Q(G)=I+R(G). 因此, 图的规范化(无符号)拉普拉斯谱可以用图的Randi´c谱表示. 根据Randi´c谱与规范化(无符号)拉普拉斯谱之间的关系, 以及定理1, 我们得到定理2和3. 定理2 设Gi是有ni个点的ri-正则图,i=1,2. 则G1⊻G2的规范化拉普拉斯谱为: 证明 首先, 根据等式(1)和定理1 (i), 得到了G的规范化拉普拉斯谱的部分特征值 其中j=2,3···n2. 其次, 根据定理1 (ii), 我们知道G1⊻G2的一些Randi´c特征值是方程(2r1+n2)x2−r1γi(G1)x−r1γi(G1)=0的两个根, 对于i=2,3,···,n1. 则G1⊻G2的规范化拉普拉斯特征值为方程的两个根: 其中γi(i=2,3,···,n1)是R(G1)的特征值. 通过化简方程(3), 我们得到 由此得出定理2 (ii)的结果. 最后, 根据定理1 (iii), G1⊻G2的一些规范化拉普拉斯特征值是方程的三个根: 通过化简, 我们得到 故定理2得证. 利用规范化拉普拉斯特征值与G的度基尔霍夫指数和生成树数目的关系,我们用G1和G2的Randi´c特征值来考虑G1⊻G2的度基尔霍夫指数和生成树数目. 推论 1 设Gi是有ni个点, mi条边的ri-正则图, i=1,2. 则G1⊻G2的度基尔霍夫指数为: 首先, 应用定理2 (i), 得到规范化拉普拉斯特征值. 因此, 度基尔霍夫指 其中j=2,3,···,n2. 因此 接下来, 通过定理2 (ii), 方程(7)的根β1, β2就是G1⊻G2的规范化拉普拉斯特征值. 其中γi(i=2,3,···,n1)为R(G1)的特征值. 因此, 根据韦达定理, 我们有 最后, 根据定理2 (iii), 我们得到δ1(G1⊻G2)=0. 即有方程 设方程(9)的另外两个根可以表示为x1, x2. 根据韦达定理, 我们有 注意到|E(G1⊻G2)| = 3m1+n1n2+m2. 结合等式(6), (8)和(10)可以得到G1⊻G2的度基尔霍夫度指数, 如式(4)所示. 推论 2 设Gi是有ni个点, mi条边的ri-正则图, i=1,2. 则G1⊻G2的生成树数目为: 证明 使用引理4 (ii), 我们知道 为了得到结果, 我们考虑G1⊻G2的规范化拉普拉斯特征值如下: 由方程(7), 我们得到 其中γi(i=2,3,···,n1)为R(G1)的特征值. 由方程(9), 我们得到 通过上述等式(12)和Пni=1di=(2r1+n2)n1rn11(r2+n1)n2, 结合等式(5), (13)和(14)可以得到G1⊻G2的生成树 数目, 如式(11)所示. 定理3 设Gi是有ni个点的ri-正则图,i=1,2. 则G1⊻G2的规范化无符号拉普拉斯谱为: 证明 定理3 可以很容易地通过定理2 的类似证明得到. 在这一节中, 我们主要考虑两个正则图的分裂S-点连接图的R-谱, L-谱, Q-谱以及一些相关的应用. 设Gi是ni个点的ri-正则图, i = 1,2. 根据定义1 (ii), G1⊼G2的点可以由V(G1)∪S(G1)∪V(G2)构成, 其中V(G1)={v1,v2,···,vn1}, S(G1)={v′1,v′2,···,v′n1}, V(G2)={u1,u2,···,un2}. 显然, G1⊼G2的点的度为: G1⊼G2的邻接矩阵和对角矩阵可按V(G1), S(G1)和V(G2)的顺序表示为块矩阵形式: 则G1⊼G2的Randi´c矩阵可表示为: 证明 G1⊼G2的Randi´c矩阵的特征多项式是 其中 则 定理4得证. 在本节中, 我们应用定理4来计算分裂S-点连接图的规范化(无符号)拉普拉斯谱, 以及度基尔霍夫指数和生成树的数目. 通过对2.2节中定理和推论的类似证明, 我们可以得到以下主要结论. 定理 5 设Gi是有ni个点的ri-正则图,i=1,2. 则G1⊼G2的规范化拉普拉斯谱为: 推论3 设Gi是有ni个点, mi条边的ri-正则图, i=1,2. 则G1⊼G2的度基尔霍夫指数为: 推论4 设Gi是有ni个点, mi条边的ri-正则图, i=1,2. 则G1⊼G2的生成树数目为: 定理6 设Gi是有ni个点的ri-正则图,i=1,2. 则G1⊼G2的规范化无符号拉普拉斯谱为: 在这一节中, 我们构造了关于Randi´c矩阵, 规范化拉普拉斯矩阵和规范化无符号拉普拉斯矩阵的几类非正则同谱图. 根据Randi´c矩阵, 规范化拉普拉斯矩阵和规范化无符号拉普拉斯矩阵的定义, 得到引理6. 引理6 如果G1和G2是R-同谱的, 则它们是L-图谱并且是Q-图谱的. 观察1 由上一节给出的所有定理可知, 所有分裂V-点、分裂S-点连接图的Randi´c(规范化拉普拉斯和规范化无符号拉普拉斯)谱取决于正则度,顶点数和图Gi(i=1,2)对应的谱.此外,我们注意到,尽管G1和G2是正则图,G1⊻G2和G1⊼G2是非正则图. 定理 7 设Gi, Hi为ri-正则图, i = 1,2, 其中G1可以与H1不同. 如果Gi和Hi是R-同谱的, i = 1,2, 则G1⊻G2和H1⊻H2是R-同谱, L-同谱并且Q-同谱的; G1⊼G2和H1⊼H2也是R-同谱, L-同谱并且Q-同谱的. 证明 根据引理6和观察1, 很容易得到定理7.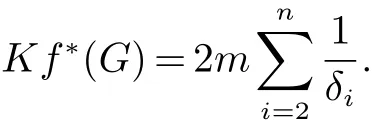
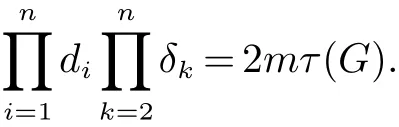

2 分裂V-点连接图的谱

2.1 分裂V-点连接图的R-谱
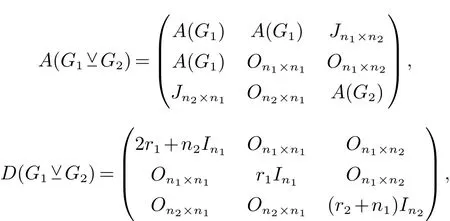
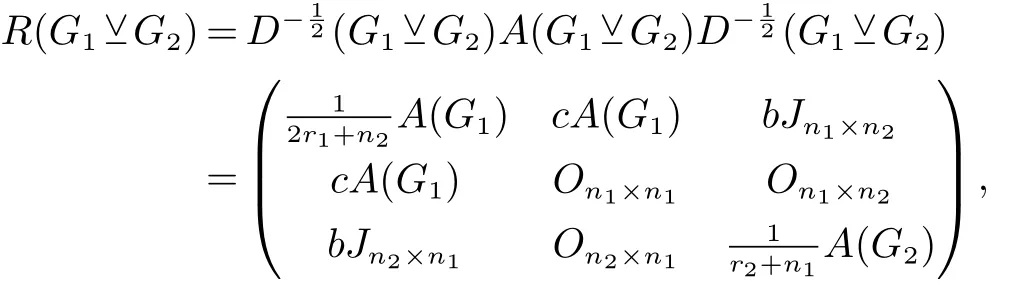

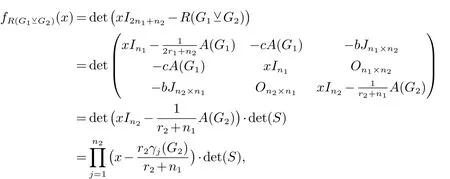

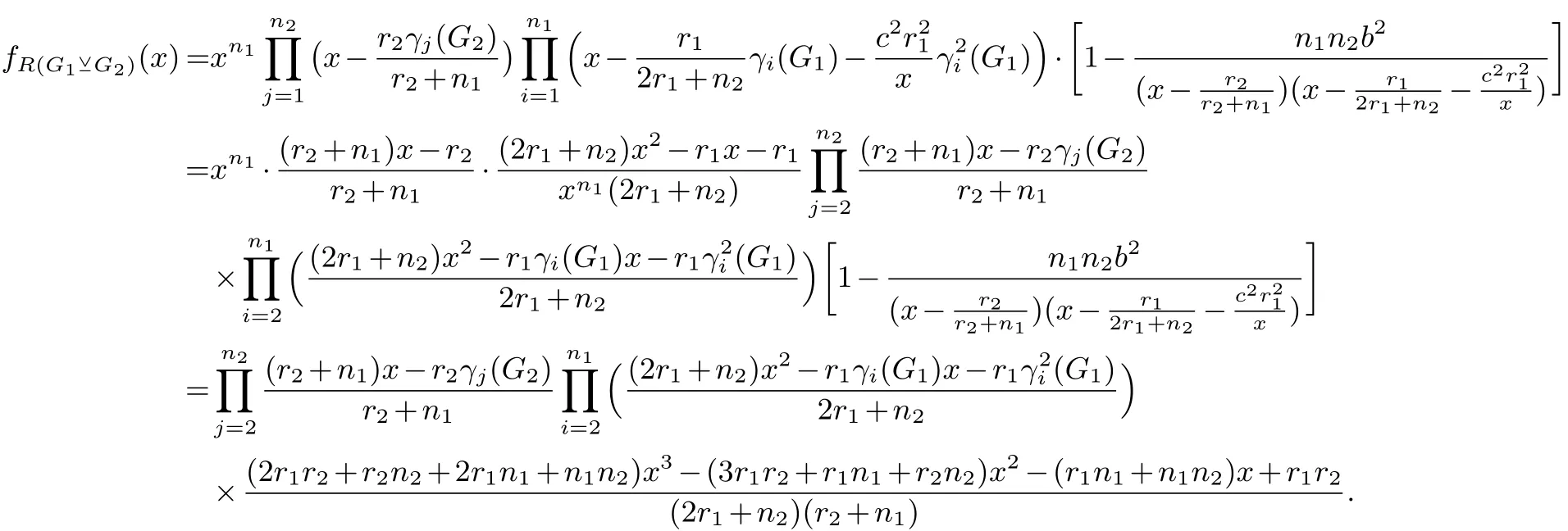
2.2 分裂V-点连接图的L(Q)-谱
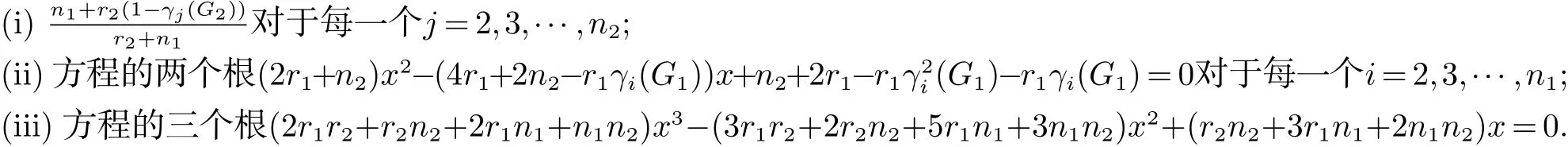
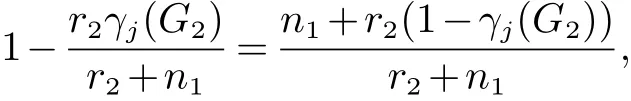
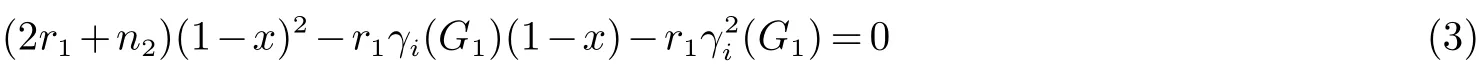
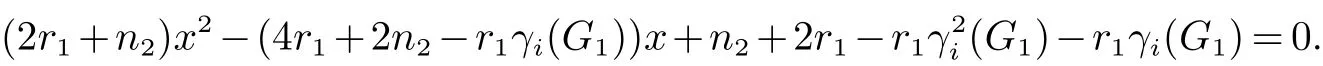



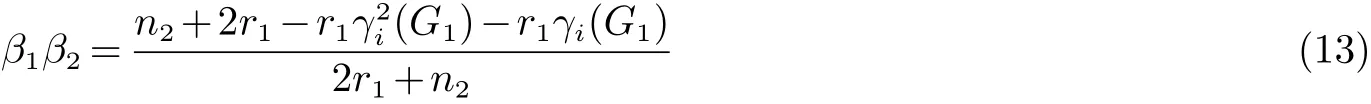

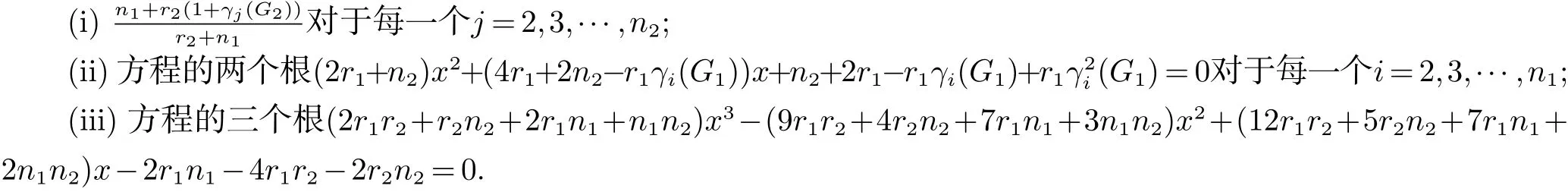
3 分裂S-点连接图的谱
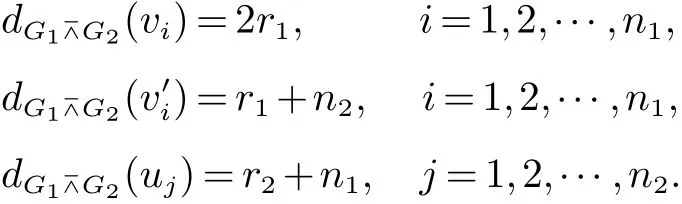
3.1 分裂S-点连接图的R-谱
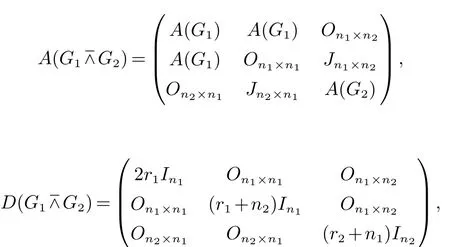

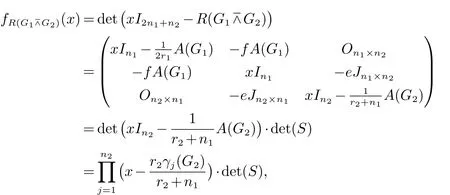

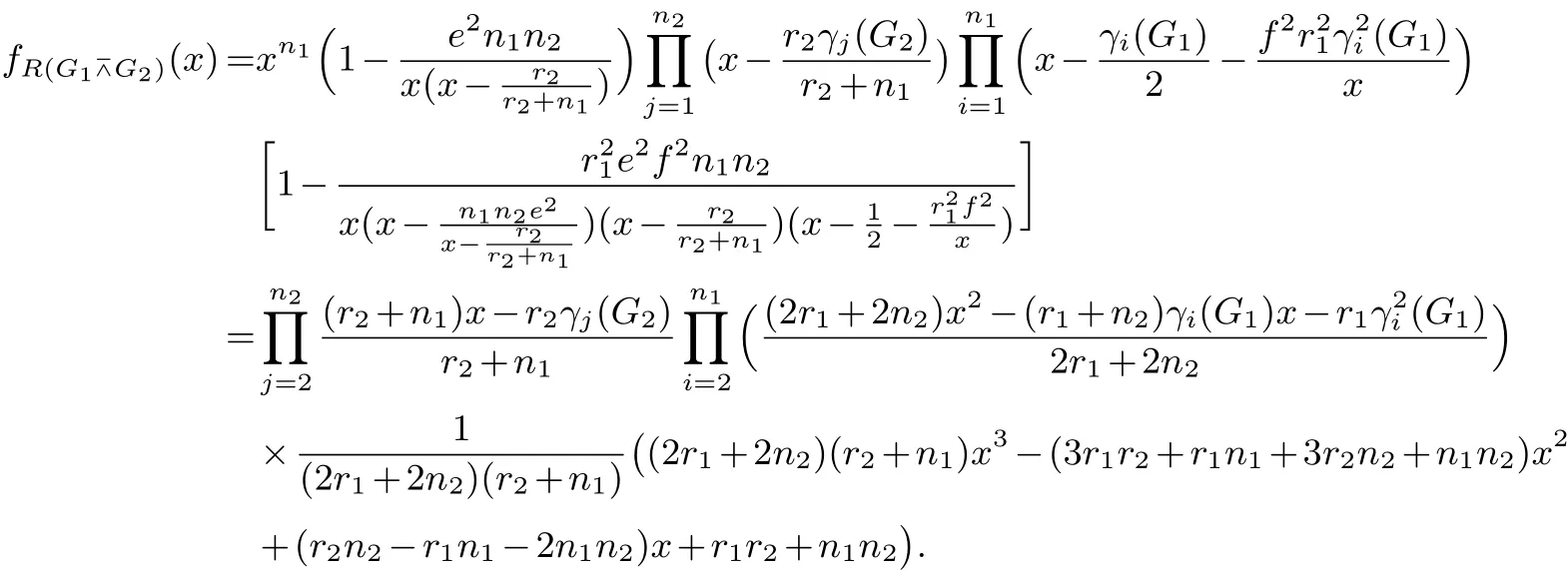
3.2 分裂S-点连接图的L(Q)-谱
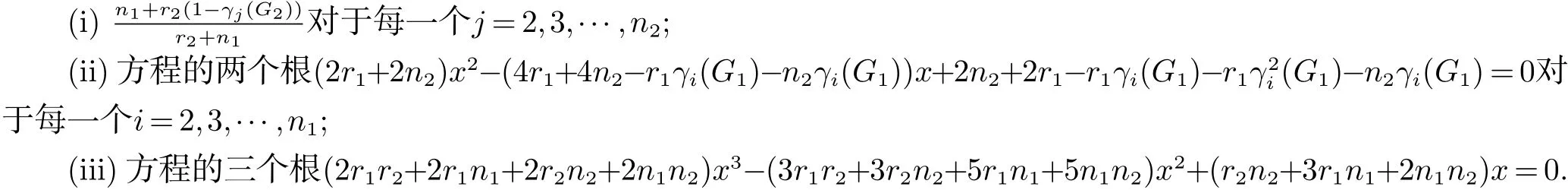
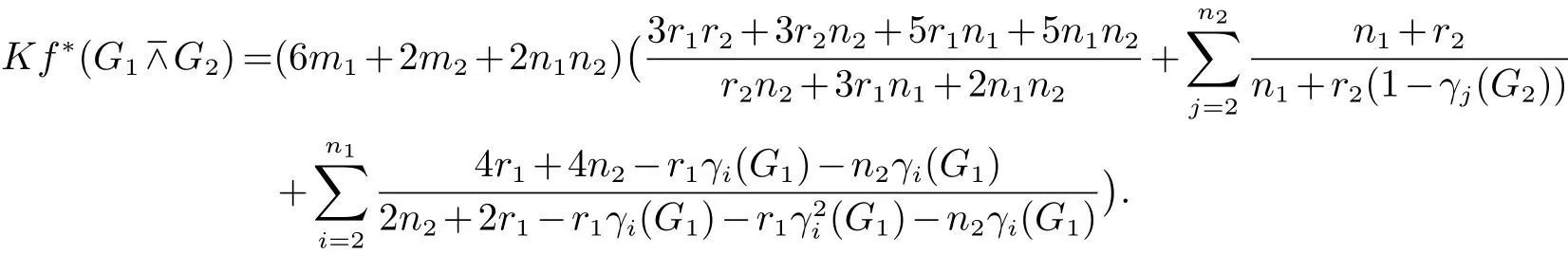
4 非正则的Randi´c(规范化拉普拉斯和规范化无符号拉普拉斯)同谱图

