具有附加弹性支承的圆形薄板结构振动分析

王 栋，朱书月

（1.西北工业大学 航空学院，西安 710072；2.中航西安飞机工业集团股份有限公司，西安 710089）

圆形薄板是典型的工程结构形式，在实际工程有广泛的应用。近年来，有关圆板结构振动特性及响应的研究已有丰富的成果，采用解析或数值方法能有效地求解圆板结构的振动问题[1－3]。这些方法的基本思路都是基于结构的边界条件，修改相应的位移试函数或插值函数来获得结构的振动特性。Liu和Lee[1]采用有限元法分析了三维圆板结构(考虑厚度)的振动频率与振型。Gupta等[2]采用微分-积分方法分析了非均质变厚度圆板结构的自由振动问题。Zhou 等[3]利用对偶法求解固有频率，从而求得了不同尺寸的圆形、环形和扇形薄板的振动特性，并与有限元数值结果进行比较，从而验证了该方法的准确性。石先杰等[4]采用谱几何法建立弹性边界条件下圆板结构横向自由振动分析模型，并将求解结果与有限元法计算、实验结果进行对比，验证了谱几何法的精确性和有效性。陈美霞等[5]研究了弹性边界条件下圆板的流-固耦合振动特性，将圆板位移展开为级数形式，并采用速度势函数描述流体运动。王忠民等[6]基于微分求积法分析了旋转圆板的横向振动和稳定性问题，对于变系数的圆板的轴对称运动微分方程，采用微分求积法离散方程和边界条件，分析了周边固支、简支和自由3 种约束条件下旋转圆板的前几阶复频率值。

对于一般的结构，支承不仅能起到固定结构的作用，还能改变结构的刚度分布及其动力学性能，有效控制结构的振动响应。对于具有附加支承的薄板结构，其相应的动力性能分析以及附加支承的优化设计研究也取得到了一定的成果。Wang[7]分析了环形支承圆板结构的振动模态，研究发现当支承沿径向发生移动时，圆板结构的模态会发生转换。Zur[8]利用拟格林函数求解了具有固支、自由和简支边界的功能梯度圆板振动频率问题。综合研究了边界约束条件、体积分数指数、环支承位置和刚度对圆板固有频率的影响。Kumar[9]总结了瑞利-里兹(Rayleigh–Ritz)法在结构静、动力分析与计算中的广泛应用。Wang 等[10]采用瑞利-里兹法对矩形板附加弹性支承的位置进行了优化设计，计算了使薄板的基频达到原系统的第2 阶固有频率所需的最小支承刚度值。通过求解特征方程的最小正值解，获得了板的附加支承在最优位置的最小刚度值。近期Wang 和Friswell[11]分析了附加支承附带质量对弹性支承最优设计的影响。然而对于圆形薄板结构附加弹性支承问题，相关的研究成果却比较少。附加支承对圆形薄板结构振动性能的影响也有待进一步深入研究和分析。

本文采用瑞利-里兹法分析计算圆形薄板结构附加弹性铰(点)支承时的振动特性，保证支承位置能在结构内能连续移动，不受有限元法网格划分的限制。采用正交梁多项式作为圆板的径向位移试函数，用完整的傅里叶级数作为圆板周向位移试函数，确保圆板结构的对称与反对称模态能完备地获取。通过与有限元计算结果的对比，验证了本文方法的正确性和有效性。随后分析了附加支承的数量、刚度和位置对圆板固有频率的影响，探讨了圆板结构第一阶固有频率与附加支承分布对称性的变化情况。

1 圆板弯曲振动基本方程

如图1 所示，假设一个厚度均匀的弹性圆环形薄板结构作横向自由振动，板内有一个弹性铰支承与基础相连。圆环形薄板的外半径是a，内半径是b，内外半径之比为c=b/a，厚度为h。在极坐标r‒θ平面内，支承位置为p(rs，θs)。根据克希霍夫薄板理论(Kirchhoff hypothesis)，在极坐标系下圆环形薄板的自由振动特征方程为[3]：

图1 圆环形薄板结构附加一个弹性支承

式中：ω表示结构的固有振动频率，D=D=是薄板的弯曲刚度，E是材料的弹性模量，μ是泊松比，ρ是材料体积密度。ks是附加支承的刚度系数，δ(∙)是Dirac Delta函数。为了避免分析计算过程中出现分母为零的情况，本文将圆形板近似成内半径b极小的环形薄板。

根据瑞利-里兹法，本文将圆(环)形薄板的横向位移函数W(r,θ)近似表达为：

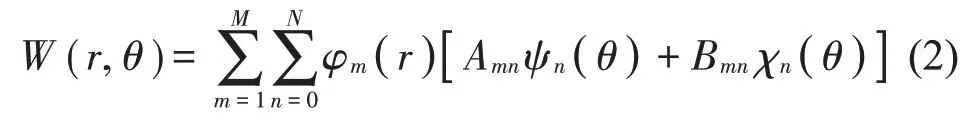
式中：φm(r)、ψn(θ)和χn(θ)分别表示圆板沿径向与周向的位移试函数，并且φm(r)至少要满足圆环板内外边界几何约束条件。M和N为沿着径向与周向位移试函数所取的项数。未知系数Amn与Bmn将由振动特征方程确定。对于弹性圆形薄板，根据其振动模态对称性的特点，本文在圆板两个方向上分别取不同形式的位移试函数。

2 位移试函数选取

2.1 径向位移试函数

采用正交梁特征多项式作为圆板沿径向的位移试函数[12]。根据圆板的内外边界约束情况，先获得等效的梁的边界约束条件，从而确定初始的位移试函数φ1(ξ)。再根据Gram-Schmidt递归过程构造其他各项位移试函数：

其中各项试函数应满足正交性条件：

根据以上条件，试函数构造式中的系数Bk和Ck分别为：

定义φ0(ξ)为0。而初始位移试函数φ1(ξ)按如下多项式分别构造：

其中的系数aj(j=1，…，5)按照圆环径向内、外边界约束，根据等效梁的边界条件确定[12]。各典型约束边界对应的系数如表1所示。

表1 边界约束条件与初始位移函数中的系数

对于圆板结构，由于采用的是内半径极小的圆环板来近似圆形薄板，因此其位移试函数的内边界全部按自由状态选取，允许圆板的圆心自由变形。实际只需考虑圆形薄板外边界的约束状况即可。

2.2 周向位移试函数

由于圆板沿周向位移函数需要满足对称性的条件，因此在式(2)中采用完整的傅里叶级数作为位移容许函数：

同时引入傅里叶级数的正弦和余弦函数，希望能很好地模拟弹性圆板的振动特性，特别是要准确获得沿圆周方向的正、反对称模态，以及重合的结构固有频率信息。

此外，所取的位移试函数项数也影响到本文所用方法计算结果的准确性，一般要根据结构振动特点设置合理的项数。经过多次试算和收敛性分析，本文在各坐标轴方向上分别选取了7 项，所得频率计算结果基本达到了稳定。

3 频率特征方程的建立

为了抑制薄板的振动水平，在保持原结构不变的情形下，可以采取附加支承的方式改变板的固有频率和振型[10]。假设铰支承是无质量的，用一个横向线弹簧表示，如图1所示。在极坐标系统下，附加一个弹性铰支承时，圆板的最大弹性势能可表示成[3]：

其最大的动能表达式为：

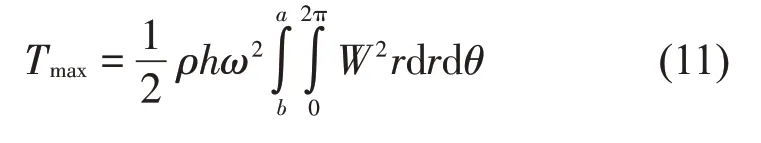
根据瑞利-里兹方法，弹性圆板结构横向自由振动的拉格朗日函数L=Umax-Tmax对系数Amn与Bmn的变化应取极值[12]：

进行无量纲化处理后即得到以下频率特征方程：

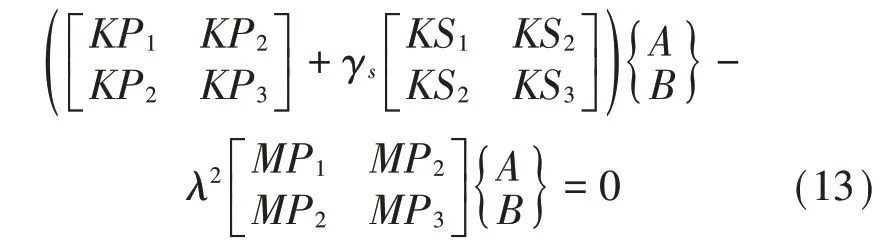
式中：无量纲化的弹性支承刚度系数γs为：

固有频率参数：

支承等效刚度矩阵中各项分别由式(16)至式(18)计算：

圆板结构刚度和质量矩阵中各项计算见本文附录。

根据以上推导结果，当附加多个铰支承时，只需要在圆板结构刚度矩阵的基础上叠加各支承的等效刚度矩阵，构成整个系统的刚度矩阵即可。通过求解频率特征方程式(13)，可得到具有支承情况下系统的固有频率与振型。若将支撑刚度系数值设为零γs=0，即可得到无附加支承时圆板结构的振动特性。此外，在给定系统的固有频率和支撑位置的情形下，还可以求解所需的附加支撑刚度[10－11]。

4 数值算例分析

为了验证本文提出的位移试函数选取结果的可行性和完备性，以及频率特征方程式(13)推导的正确性，下面对几个典型数值算例进行分析，并与有限元Ansys计算结果进行对比。采用有限元网格沿圆板径向均匀划分40个单元，沿周向均匀划分36个单元，共有144 个四节点板单元。假设弹性圆形薄板的厚度h=0.01 m，外半径a=1 m，内外半径之比c=0.000 1。材料的弹性模量E=210 GPa，泊松比μ=0.33，密度ρ=7 850 kg/m3。

4.1 附加支承对圆板固有频率的影响

考虑几种典型边界约束条件，计算附加支承在不同位置、不同刚度以及不同数量情形下圆形薄板结构的固有频率。

(1)圆心处附加1个弹性铰支承，支承刚度系数γs=2。各经典边界条件的计算结果如表2所示。

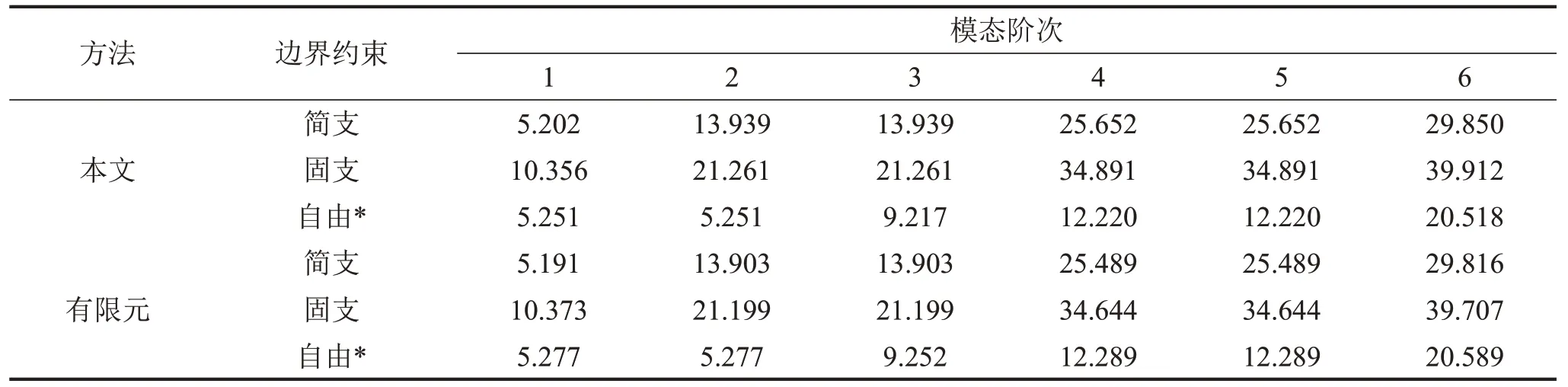
表2 圆心处附加一个弹性支承时圆板的固有频率λi计算结果

(2)边界条件为简支，在rs=0.5 m处沿周向分别均匀分布3 个(相差2π/3)或4 个(相差π/2)等刚度的弹性铰支承，如图2所示。支承刚度γs=2，计算结果如表3所示。

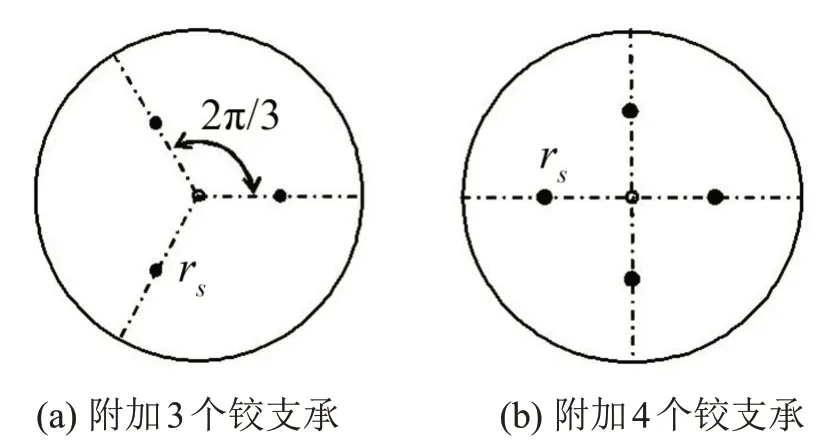
图2 圆板结构均匀附加3个或4个铰支承

(3)边界条件为简支时，在rs=0.4 m处沿周向均布4 个等刚度的弹性铰支承，无量纲支承刚度分别为γs=2和γs=5。计算结果如表4所示。

分析比较以上3 种情形的频率计算结果，可以得出以下结论：

(1)本文提出的位移试函数能够很好地模拟圆板的横向振动状况。圆板固有频率的重合情况(对应于正、反对称模态)都能被完整地呈现出来。

(2)当支承位置不在结构振型的节点或节线上时，附加支承可以使结构的固有频率升高。附加支承的数量越多，圆板结构的固有频率升高也越多，如表3 中结果所示。这是由于支承的数量越多，振动系统总体刚度越大，结构的固有频率自然会越高。

(3) 支承刚度越大，弹性圆板的固有频率也越高，如表4 中结果所示。但若将附件支承置于某一阶振型的节线上，固有频率不会因附加支承刚度的存在而改变，如表4中的第4阶固有频率。

(4)附加支承的位置对圆板结构的固有频率也会有影响。从表3 和表4 中附加4 个支承的结果可知，在支承刚度相同的情况下(γs=2)，支承位置分别在rs=0.4 和0.5 m 处，圆板结构的固有频率(特别是第1阶固有频率)升高程度并不相同。

表3 附加不同数量弹性支承时简支圆板固有频率λi计算结果

表4 附加4个弹性支承时简支圆板固有频率λi计算结果

4.2 支承位置分布对称性对圆板固有频率的影响

以下以3个附加支承为例，分别探讨其中1个支承的径向位置坐标rs以及周向位置坐标θs改变时，自由边界圆板结构第1阶固有频率变化情况。

(1)沿周向均匀分布3个等刚度的弹性支承，支承刚度γs=2。其中2 个支承固定在rs=0.5 m 处，另1个支承可沿着径向移动，如图3所示。

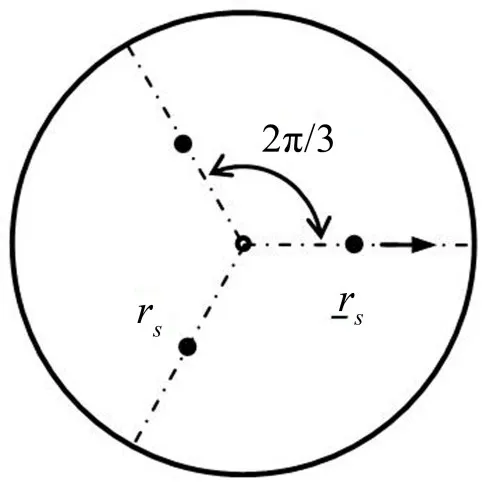
图3 自由圆板附加3个支承(其中1个支承的径向位置坐标可变)

随着其中1个支承的移动，3个附加支承的分布不再具有对称性。图4 示出了圆板的第1 阶固有频率与其中1个支承位置径向坐标变化的关系曲线。随着位置坐标从0逐渐增大，圆板结构的固有频率持续增大，当这个支承位于=0.5 m 处时，此时3 个支承的位置刚好是对称分布，结构的第1 阶固有频率上升到最大值(λ1=0.963 1)。此后随着支承的继续移动，第1阶固有频率不再改变。

图4 附加3个等刚度的支承时，其中1个支承的径向位置坐标与结构固有频率关系曲线

出现这种情况的原因是，当<0.5 m 时，第1 阶振型的节线不会通过该移动支承所在点，如图5(a)所示，因此移动该支承将影响圆板的第1 阶固有频率；当≥0.5 m 时，第1 阶振型的节线刚好通过该支承位置，移动该支承并不影响圆板结构第1 阶固有频率，如图5(b)图所示。

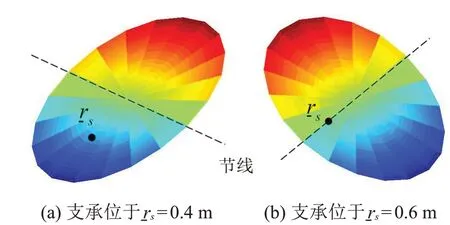
图5 支承在不同位置时自由圆板结构第1阶振型

(2)在rs=0.5 m 处，沿周向分别布置3 个等刚度的支承γs=2。其中2 个支承固定在θ=±2π/3 处，另1个支承在θ=0 轴线附近沿周向移动，即该支承周向坐标θs可变，如图6所示。

图6 自由圆形薄板附加3个支承(其中1个支承的周向坐标θs可变)

图7 示出了圆板的第1 阶固有频率随其中1 个支承周向位置坐标θs变化的曲线。

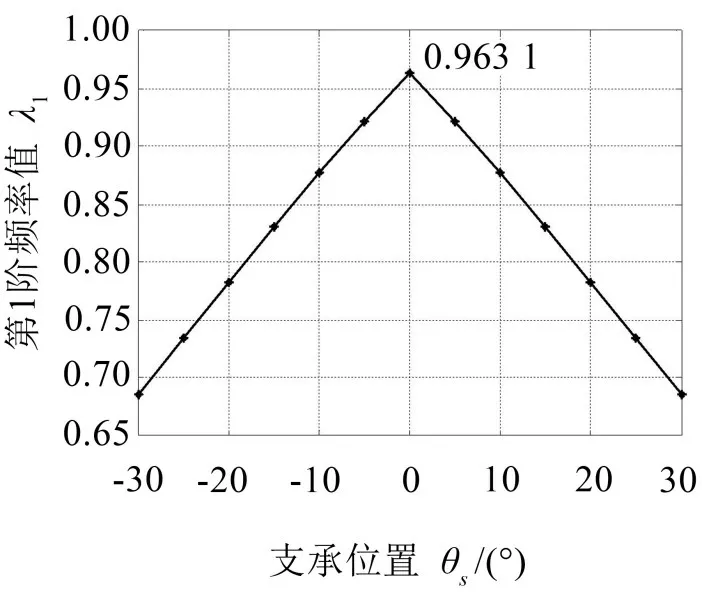
图7 附加3个等刚度的支承时，其中1个支承的周向位置坐标与结构固有频率关系曲线

可见，支承周向位置偏移对圆板结构第1 阶固有频率影响较大。只有当这个支承位于θs=0 的位置，即3个附加支承沿周向对称分布时，圆板结构的第1 阶固有频率才达到最大值(λ1=0.963 1)。否则，圆板结构的第1阶固有频率会显著下降。

由以上计算结果可知：附加支承沿径向和周向分布状况对圆形薄板结构第1阶固有频率有很大的影响。只有当附加支承的分布具有对称性时，圆板结构的第1阶固有频率值才能达到最大值。若由于某种客观原因支承无法对称分布时，圆板结构的第1阶固有频率有可能会显著下降。因此应尽量保持支承靠近对称点，以使附加支承能充分发挥作用。

5 结语

本文采用瑞利-里兹法计算了圆形薄板附加支承时，不同约束边界条件下结构的固有频率。用正交梁多项式作为圆板径向位移试函数，用傅里叶级数作为圆板周向试函数，保证计算结果的完备性和正确性，准确模拟圆板结构固有频率的重合现象。

计算结果表明：

(1)附加支承的刚度、数量和位置与结构的力学性能紧密相关。改变附加支承的设计对结构的振动特性会有很大的影响。

(2) 在支承刚度、数量等其他条件不变的情况下，对称分布的支承布局可以更有效地提高结构的固有频率。