变参数线性跟踪微分器及其在地平式大视场望远镜中的应用

杨晓霞，邓永停，赵金宇，张 斌

（中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033）

1 引 言

自抗扰控制方法（Active Disturbance Rejection Control，ADRC［1-2］）是一种基于过程误差来抑制或消除误差的控制方法，在工业和工程领域得到了广泛的应用［3-8］。跟踪微分器（Tracking Differentiator，TD［9］）是自抗扰控制方法的一个主要组成部分，主要用于对不连续或带随机噪声的信号提取连续信号及微分信号。大量的理论研究工作针对TD 的收敛性［10-11］、微分信号的提取能力以及滤波能力［12-14］展开，很多TD 的改进形式［15-16］被提出并应用在不同领域中［17-18］。事实上，TD 的一个主要作用是用于对控制系统中的参考信号进行过渡过程安排，过渡过程信号作为参考信号和反馈信号之间的一个桥梁，当参考信号发生大的跳变时，仍然能够保证反馈信号跟踪一个连续渐变的过渡过程信号，从而使得控制误差不会出现大的跳变，进而保证控制系统的稳定性和鲁棒性。

TD 又分为线性TD（Linear TD，LTD）和非线性TD（Nonlinear TD，NLTD）。在安排过渡过程时，LTD 的优点在于算法复杂度低，简单易实现，缺点在于跟踪不同幅值的阶跃信号时，需要调节快速因子参数，否则容易造成LTD 输出信号的速度和加速度过大或者过小，起不到过渡作用。NLTD 的优点在于通过使用最速控制综合函数，使得在一定加速度的限制下能够最快地跟踪参考输入，但是其算法复杂度高、计算量大，并且在跟踪不同幅值的阶跃信号时也存在输出速度过大或过小的问题。

在使用跟踪微分器安排过渡过程时，应该使得输出的过渡过程信号的速度、加速度与物理系统的反馈能力相匹配，否则，过渡过程信号变化太快起不到过渡作用，变化太慢会影响系统的最大跟踪能力。本文研究了一种带速度和加速度饱和限制的变参数线性跟踪微分器，它既能够在参考信号和反馈信号之间起过渡桥梁的作用，又能够充分发挥受控物理对象的最大速度和最大加速度能力。

2 TD 性能分析

经典的安排过渡过程的工具是LTD 和NLTD。

2.1 线性跟踪微分器

LTD 的离散形式如下：

其中：p0为设定值，h是离散化的采样步长参数，r1为快速因子，是系统唯一的可调参数，它决定系统的收敛速度。当设定值p0(k)≡p0为常值时，定义x1第一次到达0.99p0的时间为过渡时间T0，定义VmaxLTD和amaxLTD分别是LTD 输出的最大速度和最大加速度，也就是VmaxLTD=max(|x2|)，amaxLTD=max(|ẋ2|)，表1给出了LTD 的最大速度和最大加速度与参数和设定值之间的关系。

表1 LTD 的最大速度和最大加速度与参数的对应关系Tab.1 Relationship among VmaxLTD，amaxLTD and parameters

使用MATLAB 的数据拟合工具，可以得到拟合表达式：

图1 给出了当p0=1 时离散计算结果与拟合函数曲线之间的关系。可以看出，过渡过程时间T0与参数r1成反比，并且与最终的稳态响应值没有关系，这说明使用LTD 安排过渡过程时，只要参数r1确定，跟踪稳态值1 和跟踪稳态值100 或者10 000 的时间是相同的，这就导致LTD 给出的VmaxLTD和amaxLTD均与稳态值p0相关，p0越大，VmaxLTD和amaxLTD越大，而如果VmaxLTD和amaxLTD远远超过物理系统的反馈速度和加速度能力，那么物理系统的反馈信号就无法跟踪LTD 所给出的过渡过程信号，此时LTD 所给出的信号就起不到过渡作用。

图1 T0，VmaxLTD，amaxLTD 与LTD 参数r1的关系Fig.1 Relationship between T0，VmaxLTD，amaxLTD and r1

另一方面，通过简单地在LTD 的输出信号上加入速度和加速度饱和环节，是不能够解决这个问题的，因为通过仿真计算可以看出，此时LTD 的输出会发生振荡。设p0=100，r1=15，h=0.001，根据式（2）可以推算出LTD 给出的最大速度和最大加速度如下：

设物理系统反馈的最大速度Vmax和最大加速度amax如下：

图2 给出了加入式（4）的速度和加速度上界后LTD 的输出曲线。

图2 带速度和加速度饱和限制的LTD 输出Fig.2 Output of LTD with speed and acceleration saturation

2.2 非线性跟踪微分器

离散最速跟踪微分器利用fhan 函数实现，它的加速度通过参数r限定，具体形式如下：

其中：h是采样周期，r是快速因子，h0是滤波因子，可以大于采样周期h，fhan 是非线性函数，具体形式如下：

其中：fsg(a，d)=(sgn(x+d)-sgn(x-d))/2，sgn(·)是符号函数。经过计算可以得到T0，VmaxN-LTD以及amaxNLTD与参数r和p0的关系如下：

其中VmaxNLTD和amaxNLTD分别是NLTD 的最大速度和最大加速度。可以看出，NLTD 的加速度是具有上限的，但是最大速度跟稳态值p0有关，没有上限，因此带有速度饱和Vmax的NLTD 设计如下：

与LTD 不同，给NLTD 加入速度饱和限制之后不会引起信号的波动。图3 给出了带有速度饱和的NLTD 输出曲线，其中p0=100，Vmax=21，r=12，h=0.001，h0=0.01。

图3 带速度饱和的NLTD 输出Fig.3 Output of NLTD with speed saturation

带有速度饱和的NLTD 可以给出与物理系统反馈能力相匹配的过渡过程信号，在实现过渡作用的同时能够充分发挥系统的最大反馈能力。但是，由于非线性函数fhan 的计算比较复杂，不利于在工程中的实时实现。本文给出一种变参数LTD，合理地将参数r设计为跟踪误差的函数，克服了LTD 的不足，并且比带有速度饱和的NLTD 更简单易实现。

3 变参数线性跟踪微分器设计

连续的VLTD 设计如下：

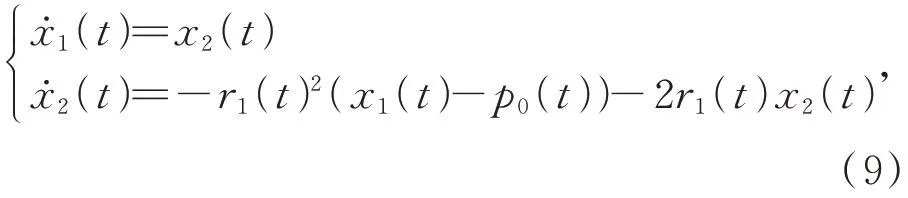
其中时变参数r1（t）设计如下：

其中：r可以设计为反馈物理信号的最大加速度，σ≥1 是唯一的可调参数。将式（10）代入式（9）可以得到VLTD 的一般形式如下：

可以看出，VLTD 与LTD 的区别在于将快速因子设置为一个时变函数，它设计为跟踪误差的减函数，以此保证初期跟踪误差非常大时，过渡过程的加速度也不会非常大。当跟踪误差小于1 时，VLTD 就变为LTD。

3.1 VLTD 的收敛性分析

对VLTD 的收敛性进行分析，得到如下定理。

定理1，设p0是常值，对于任意的初值x1（0）和x2（0）=0，VLTD 都能在有限时间内收敛至线性区间内，其中线性区间定义为跟踪误差的绝对值小于1 的区间。

证 明：设z1(t)=x1(t)-p0，z2(t)=x2(t)，σr=σ，那么VLTD 可以简化为：

因此只需证明对于任意的z1(0) 和z2(0)=0，存在时间点tc＞0 使得|z1(tc)|＜1。

情形1：如果|z1(0)|＜1，那么当t＞0 时系统的变化规律如下：

上述微分方程的解如下：

由于z2(0)=0，所以有：

对于情形1，当系统的初值处于线性区间时，系统始终处于线性区间内。

情形2：如果z1(0)≥1，那么系统的变化规律如下：

整理第二个方程得到：

在时间区间[0，τ]上对等式两边进行积分，得到：

进一步整理得：

将式（19）在时间区间[0，t]上进行积分，得到：

如果存在时间点tc∈[0，t]，使得z1(tc)＜1，那么结论成立。而如果对于任意的τ∈[0，t]都有z1(τ)≥1，那么：

整理式（21）得：

显然，不等式的右边是关于t的二次函数，当t＞4(-1)/σr时，式（22）的右边相对于t是一个单调递减函数，并且：

因此，一定存在tc＞0，使得：

从而有：

结论成立。

情形3：如果z1(0)≤-1，那么系统的变化规律如下：

整理第二个方程可得：

将 式（27）的 两 端 在 时 间 区 间[0，τ] 上 积分得：

进一步整理得：

将上述方程的两边在时间区间[0，t]上积分得：

如果存在tc∈[0，t]，使得z1(tc)＞-1，那么结 论 成 立。如 果 对 于 任 意 的∀τ∈[0，t]都 有z1(τ)≤-1，那么有：

因此有：

显然，不等式右边是一个关于t的二次函数，当t＞时，不 等 式 右 边 是 一个关于t的单调递增函数，并且有：

所以存在tc＞0，使得：

因此有：

定理结论成立。

上述结论说明，对于任意的初值x1（0），VLTD 必定能在有限时间内收敛至线性区间内。

3.2 VLTD 的速度和加速度上限分析

设tvmax为VLTD 到达速度上限的时间点，那么有ẋ2(tvmax)=0，也就是：

进一步整理得：

如果|x1(tvmax)-p0|＜1，那么有：

如果|x1(tvmax)-p0|≥1，那么有：

也就是：

根据VLTD 的特点，|x1(tvmax)-p0|≥p0/2，因此VLTD 的最大速度满足：

不等式（40）说明当|x1(tvmax)-p0|≥1 时，VLTD 的速度输出最大值不存在上限。

另一方面，可以推导出VLTD 在初始时刻达到最大加速度σ2r，并且减速阶段的加速度明显比加速阶段的加速度小。为了避免VLTD 减速阶段的加速度过小，一般选取参数σ＞1，这样就会导致加速阶段的加速度会超过物理系统的最大反馈加速度，因此，在VLTD 的加速度输出上加入加速度饱和上限即可。

通过上面的分析可知，有必要对VLTD 的速度和加速度输出加入饱和限制，记x3为VLTD 的加速度输出，VmaxVLTD为VLTD 的速度上限，那么带有速度和加速度饱和限制的离散VLTD 形式设计如下：

3.3 仿真设计

设物理系统的最大速度和最大加速度分别为Vmax=20 和amax=12，VLTD 的参数取值如下：采 样 步 长h=0.001，σ=2.3，r=12，速 度 上 限VmaxVLTD=20，加速度上限为r，稳态响应值p0=100，50，10，1，图4 分别给出了加入速度和加速度限制前后的VLTD 输出对比曲线。可以看出，加入速度和加速度饱和限制之后，VLTD 的收敛性没有受到影响，而且在p0较大，也就是VLTD 本身输出的最大速度超过VmaxVLTD时，速度饱和才起作用；而在p0较小时，也就是VLTD 本身输出的最大速度不超过VmaxVLTD时，速度饱和不起作用。一旦σ确定之后，无论p0取值如何，加速度饱和都会起作用，因为只要σ＞1，那么初始段的加速度一定会大于r。

图4 速度及加速度饱和对VLTD 输出的影响Fig.4 Impact of speed and acceleration saturation on output of VLTD

将带速度和加速度饱和的VLTD（41）与带速度饱和的NLTD（7）进行比较，其中VLTD 的参数取值与上面仿真相同，NLTD 的参数取值为r=12，h0=0.01，稳态值p0取为100，图5 给出了两者的对比曲线。可以看出，VLTD 可以达到与NLTD 几乎相同的效果，并且从加速度曲线上可以看出，在接近稳态值时，VLTD 的加速度曲线更平滑，这有利于反馈信号的平稳快速地跟踪。另外，VLTD 的计算复杂度远远小于NLTD，在使用时能够节省计算内存空间，有利于算法的实时性。

图5 VLTD 和NLTD 输出曲线的对比Fig.5 Comparison of output between VLTD and NLTD

4 VLTD 在地平式大视场望远镜中的应用

4.1 地平式大视场望远镜搜索路径分析

大视场望远镜主要针对地球同步轨道（GEO）、同步转移轨道（GTO）及中高轨（MEO）的目标进行搜索、捕获、跟踪和测量。不同轨道的目标特性不同，相应的工作模式有所不同。由于极轴式望远镜受结构设计的限制，望远镜口径不宜过大，因此将米级大视场望远镜设计为地平式结构。由于地平式望远镜方位轴和俯仰轴的耦合作用，无论何种工作模式都会牵扯到方位轴的频繁变步长调转，即使是对固定赤纬的目标进行搜索。

本文以GEO 目标为例进行说明，GEO 目标的星下点赤纬范围为±15°，设观测站址的经纬度为(ϕs，σs)，A是地平式望远镜的方位角，E是地平式望远镜的俯仰角。以望远镜俯仰角大于10°作为目标可观测的判别条件，可以计算出观测站能有效观测±15°赤纬带的GEO 目标的星下点经度为σs±σ0的目标，其中σ0由站址纬度ϕs决定。以两个不同纬度的站址为例，设ϕs1=24°N，ϕs2=46°N，望远镜视场为2.5°×2.5°，搜索路径采取“Z”字型模式，以星下点纬度不变，经度以2.5°作为阶跃步长，计算在不同纬度观测站观测±15°赤纬带目标时方位角和俯仰角的变化情况，并且分别计算了每次调转时方位角和俯仰角分别调转的步长，得到的曲线如图6 和图7所示。

图6 ϕs1=24°N 时方位角和俯仰角的变化规律Fig.6 Variation of azimuth and elevation angles with ϕs1 of 24°N

对比图6 和图7 可以看出，观测站点纬度越低，观测GEO 目标带的俯仰角越大，能有效观测的目标带经度范围就越大，调转单个视场时，方位角需要调转的步长就越大。对于地平式望远镜来说，即使固定步长扫描同一赤纬的空间目标，方位轴仍是进行变步长的位置调转。另外，由于地平式望远镜两个轴的耦合运动，即使扫描同一赤纬的空间目标，望远镜的俯仰角并不是固定不变的，而是需要进行变步长的位置调转，上述两种情况中俯仰轴分别进行了0～2°不等的位置调转。在跟踪模式下，当切换被跟踪目标时，也需要调转方位轴和俯仰轴位置，而且调转的步长与所切换的两个目标的相对位置有关。

图7 ϕs2=46°N 时方位角和俯仰角的变化规律Fig.7 Variation of azimuth and elevation angles with ϕs2 of 46°N

4.2 传统的位置环分段控制模式

对于地平式大视场望远镜来说，无论是进行搜索模式还是跟踪模式，都会频繁涉及到望远镜两个轴的变步长位置阶跃，而且阶跃步长大小不一。传统的望远镜主轴控制，一般对位置控制环采用分段控制的方式，当位置误差较大时，位置环输出常值；当位置误差较小时，则进行闭环解算。位置环输出的具体形式如下：

其中：i=1，2，...，N，ω*是位置控制环的输出，eθ=θref-θ是位置误差，θref是位置参考值，θ是位置反馈值，θ0＜θ1＜…＜θN是预设的阈值，ω1＜ω2＜…＜ωN+1是位置控制环输出的常值，Cθ是位置闭环控制器。该方法的缺点在于分段的过程比较依赖经验值，例如θi，ωi以及分段数N的选择都需要通过多次试验，才能使所设计的分段参数与物理系统的实际响应相匹配，否则如果切入闭环的速度过大或者过小，都会影响系统的响应品质。另外，一旦物理系统的最大速度或者最大加速度发生改变（例如系统的转动惯量发生改变、或者驱动器的驱动电流、驱动电压发生改变等），均需要对分段进行重新设计，否则会出现因分段与系统响应能力不匹配所造成的响应过慢或者超调等现象。

4.3 VLTD 在地平式大视场望远镜快速定位中的应用

将带有速度和加速度饱和限制的VLTD 应用于望远镜轴系的快速调转定位中，并且与传统的位置分段控制方式进行对比实验。实验对象是某1 m 级地平式大视场望远镜的方位轴，轴系采用交流永磁同步电机驱动，驱动器和控制器硬件平台采用DSP+FPGA，驱动电源采用48 V 的开关电源，驱动电流的最大值为10 A，位置反馈信号采用29 位绝对式编码器测量，速度反馈信号通过位置反馈信号差分并滤波后得到，控制方式采用电流+速度+位置的三闭环方式，控制框图如图8 和图9 所示。其中，图8 的位置环采用传统的位置分段控制方式，图9 的位置环采用VLTD进行位置参考信号的过渡。除了位置误差的处理方式不同，两者的三环控制器设计完全相同，电流控制器的设计采用传统的PI 控制器，速度环控制器采用ADRC 控制方式，具体设计方法见文献［19］，此处不再赘述，位置环控制器采用最简单的比例控制器。

图8 采用位置分段的控制框图Fig. 8 Control diagram of position section method

图9 采用VLTD 的控制框图Fig. 9 Control diagram of VLTD method

在进行位置环分段以及VLTD 的设计之前，均需要对系统的最大反馈能力进行摸底测试，得到系统的最大反馈速度为20.5（°）/s，最大加速度约为19.6（°）/s2。在不存在机械限位的前提下，根据就近调转原则，方位轴的最大调转步长为180°。为了验证系统对不同步长的位置响应能力，用两种实验方法分别进行2°～180°之间不同阶跃步长的位置阶跃实验，其中位置环分段参数 取 值 为：N=8，θ0=0.01°，θ1=0.017°，θ3=0.28°，θ4=1.1°，θ5=2.2°，θ6=11°，θ7=22°，θ8=33°；ω1=0.1(°)/s，ω2=0.2(°)/s，ω3=0.5(°)/s，ω4=1.9(°)/s，ω5=3.8(°)/s，ω6=5.3(°)/s，ω7=11.8(°)/s，ω8=16.7(°)/s，ω9=20(°)/s。

图10～图13 分别给出了几个典型的实验结果，其中p0=2°，10°，30°和180°。可以看出，使用位置分段的方式均能够达到无超调的响应效果，但是由于分段的设置，在减速的过程中不能够充分发挥系统的最大减速能力，所以减速段的时间明显变长。

图10 当p0=2 时的位置阶跃响应Fig.10 Position step response with p0=2

图11 当p0=10 时的位置阶跃响应Fig.11 Position step response with p0=10

图12 当p0=30 时的位置阶跃响应Fig.12 Position step response with p0=30

图13 当p0=180 时的位置阶跃响应Fig.13 Position step response with p0=180

使用VLTD 过渡的实验中，参数取值为h=0.001，σ=2.3，r=19，Vmax_VLTD=20。为了验证VLTD 的输出速度作为速度前馈的作用，分别完成了带有速度前馈和不带有速度前馈的实验，几组典型的实验结果如图14～图17 所示。从实验结果可以看出，使用带速度和加速度限制的VLTD 安排的过渡过程能够按照预设的速度和加速度引导望远镜轴系运动，在加速和减速段都能够充分发挥出系统的反馈能力。

图14 当p0=2 时的位置阶跃响应Fig.14 Position step response with p0=2

图15 当p0=10 时的位置阶跃响应Fig.15 Position step response with p0=10

图16 当p0=30 时的位置阶跃响应Fig.16 Position step response with p0=30

图17 当p0=180 时的位置阶跃响应Fig.17 Position step response with p0=180

表2 列出了实验中位置响应进入5″误差带的时间t1和1″误差带的时间t2，它定量地描述了不同实验方法的效果。可以看出，使用VLTD 安排过渡过程的方式可以使得动态响应时间明显变短，并且利用VLTD 的第二个输出作为速度前馈能够进一步缩短响应时间，与位置分段方法相比，响应时间缩短了大约15%～37%，有效地提高了望远镜的搜索效率，对于大视场望远镜具有重要的意义。

表2 位置响应进入5″和1″误差带的时间Tab.2 Time points for position response in 5″and 1″position error bands （s）

对比实验中只给出了一种分段取法，虽然通过增加分段数N以及优化分段策略可以进一步提高该方法的响应速度，但是优化过程需要进行大量的实验，而且分段数N越多，程序的计算复杂度越高，也不利于程序的二次移植。而本文给出的VLTD 设计方法，参数设定方法简单，只需测量物理系统的最大反馈速度和加速度，就可以进行参数的设定，且程序可以进行快速移植。

5 结 论

本文给出了一种为物理信号安排过渡过程的工具——变参数线性跟踪微分器，它是在分析已有线性跟踪微分器安排过渡过程的不足基础上提出的，所给出的过渡过程能够很好地与物理系统的反馈能力相匹配，在起到过渡作用的同时，又能够充分发挥系统的最大反馈能力。从理论上对VLTD 的收敛性进行了证明，并且给出了仿真计算。将VLTD 应用于地平式大视场望远镜的快速调转控制中，替代传统的位置环基于位置误差的分段控制方式，实验结果表明，在各种不同大小步长的位置阶跃响应中，响应时间可以缩短大约15%～37%，大大提高了望远镜的搜索效率。所设计的安排过渡过程方法的参数简单易设置，利于在工程中的调试和实现。

本文中的分析以及实验均是针对常值信号进行的，VLTD 也可应用于对时变信号的过渡过程安排，在后续工作中会对VLTD 跟踪时变信号的性质进行分析。