长期水平荷载对单桩式海上风机结构自振频率的影响分析

孙毅龙， 许成顺， 席仁强,2， 杜修力， 豆鹏飞,3

(1. 北京工业大学 城市与工程安全减灾教育部重点实验室，北京 100124； 2. 常州大学 机械工程学院， 江苏 常州 213164； 3. 清华大学 水利水电工程系，北京 100084)

在海上风能的开发与利用中，风机结构整体自振频率是海上风机设计中的主要难点之一。目前工程中均采用“软-刚”模式进行海上风机结构和基础的设计[1-2]，即海上风机结构系统自振频率介于1P频率(发电机转动频率)带和3P频率(叶片扫掠频率)带之间。但由于1P频率带和3P频率带之间范围较小，因而对海上风机整体结构自振频率的设计要求较高。

为准确地计算海上风机整体结构自振频率，国内外学者开展了相关研究。Zaaijer[3]推导了简化解析方法，研究了单桩式海上风机结构的振动特性及地基刚度对海上风机整体结构自振频率的影响。Byrne[4]将地基与基础、上部结构的相互作用简化为一个旋转自由度的弹簧，顶部简化为集中质量，从而建立了海上风机结构整体自振频率的简化计算方法。Bhattacharya等[5-6]将基础与地基间的相互作用简化为水平刚度弹簧和摇摆刚度弹簧，上部结构等效为Euler-Bernoulli梁，从而建立结构自振频率的求解方法，并与模型试验、有限元计算进行了对比。黄茂松等[7]采用类似的桩土相互作用简化方法，建立群桩基础支撑的海上风机结构的频率分析模型。上述学者建立的结构自振频率计算方法形式简单，但基础刚度的确定较为复杂。因而Andersen等[8-10]将桩土相互作用简化为温克尔弹簧，建立了单桩式海上风机结构整体自振频率计算方法。

然而海上风机结构所处的荷载环境特殊，在其运营周期内将长期承受风、波浪等循环荷载作用[11]，同时面临风暴、地震等极端荷载的威胁，因而地基土物理力学特性会发生改变。Achmus等[12-14]基于室内土体循环三轴试验，建立了考虑长期循环荷载效应的单桩数值模型，发现长期循环荷载作用会导致桩周土体参数发生变化。Nikitas等[15]采用动单剪仪，开展长期循环荷载下砂土模量、变形的变化规律研究，发现循环前期土体密实剪切模量增大，随后逐渐趋于稳定，但该研究中未考虑桩基对土体参数变化的影响。Bayat等[16-17]基于建立二维饱和两相介质计算模型，发现循环荷载作用会引起桩-土相互作用刚度的降低，但考虑的循环荷载加载次数较少。Cuéllar等[18-20]开展了地基土微观机理变化研究，发现桩周土体反应在长期循环荷载作用前期表现为挤密，后期加载中桩周土体产生棘轮效应。在海上风机运营期间，桩周土体弹性模量等关键参数的较大改变，会对桩基承载特性、海上整体结构动力特性产生显著的影响[21-22]。Lombardi等[23-24]开展了单桩式海上风机结构水平循环荷载模型试验，验证了风机结构自振频率的偏移现象；最大偏移量达30%以上。Carswell等[25]基于p-y曲线模型，分析了黏土刚度变化对海上风机结构整体自振频率的影响，发现黏土刚度的退化导致风机系统整体自振频率向1P频率偏移。

综上所述，地基土物理力学特性的变化会导致风机结构系统自振频率发生偏移现象，因而在海上风机结构自振频率设计计算中，应考虑长期循环荷载对海上风机结构自振频率的影响，但现有的研究却鲜有报道。本文基于动力运动方程，考虑桩土相互作用，通过嵌入地基刚度衰减模型考虑长期循环荷载引起的地基刚度变化，建立单桩式海上风机结构自振频率的简化计算方法，探讨循环荷载大小、加载次数对海上风机结构自振频率的影响规律；为工程设计提供参考。

1 数值算法的建立

1.1 考虑桩土相互作用的自振频率计算方法

单桩基础是当前海上风电场中常用的基础型式，因此本文计算方法的建立主要针对单桩基础。由于风机塔筒为变截面，因此塔筒离散为若干段，桩土相互作用简化为水平地基弹簧，风机、扇叶等简化为集中质量，计算模型示意图如图1所示。

图1 简化模型示意图Fig.1 Diagram of simplified model

根据结构动力学中，有阻尼体系的自由振动运动方程如下[26]

(1)

式中：M为质量阵；C为阻尼阵；K为刚度阵；u为计算方向的位移向量。

采用集中质量法，将海上风机上部结构化为多自由度体系，取桩基、结构等简化为的节点质量mi构造质量矩阵M，如下

(2)

阻尼矩阵按照经典的Rayleigh阻尼构造为对角矩阵

(3)

因而在未考虑地基土阻尼时，阻尼矩阵如式(4)所示。其中ξ为钢材料的阻尼系数，取为2%；本文主要研究海上风机结构系统的自振频率，因而ω为结构的一阶频率。

C=2ξϖM

(4)

桩土相互作用简化地基弹簧中地基阻尼取为[27]

(5)

式中：ξs为土体的阻尼比；ρs为土体的密度；Vs为土体的剪切波速；D为桩基直径；a=ωD/Vs；ki为地基土刚度。

参考黄茂松等和杨春宝等的方法，构造刚度矩阵K为

(6)

(7)

(8)

(9)

桩土相互作用的水平地基刚度kxi选取p-y曲线的初始地基刚度，由于海上风机单桩基础的桩径较大，其尺寸效应显著[28]，因而本文方法中的地基刚度参照作者在文献[29]中建立的修正地基刚度，如式(10)所示。将kxi添加到刚度矩阵K地基部分的剪切刚度项中，形成考虑桩土相互作用的的整体刚度矩阵。

(10)

式中：nh在不同场地下的取值参照图2；D0为相对桩径，取1 m；zi为土体深度，m；z0为相对深度，取2.5 m；m，n为影响指数，取值参照文献[30]。

图2 地基模量常数nh与相对密实度的函数关系Fig.2 Constant of subgrade reaction nh versus relative density

将上述矩阵集成、组装，代入式(1)中，得整体振动方程，先求解无阻尼下的自振频率，再代入根据式(4)和式(5)计算有阻尼下的自振频率。该计算方法与杨春宝等的自振频率求解方法原理是一致的，不同的是地基刚度考虑了桩径的增大对地基刚度的影响。

1.2 考虑砂土刚度衰减的自振频率计算方法

海上风机单桩基础在风、波浪等循环荷载作用下，桩周土体的模量等参数会发生变化，如图3所示。为描述土体的该特性，Huurman[31]开展了土体三轴试验，提出了砂土在长期循环荷载下的刚度衰减模型，砂土的割线模量与加载次数也为指数型函数关系，具体如下

图3 循环荷载下砂土的割线刚度衰减示意图Fig.3 Diagram of degradation of sand secant modulus under cyclic loading

(11)

(12)

式中：EsN为循环荷载加载N次下砂土的割线模量，kPa；Es1为循环荷载第一次下的土体割线模量(土体的初始弹性模量)；N为循环荷载加载次数；a，b为刚度衰减模型参数，其中，密实砂土，a为0.20，b为5.76，中密砂土，a为0.16，b为0.38[32]；X为砂土的循环应力比；σ1,cyc为土体循环周期的最大主应力，kPa；σ1,sf为土体静力破坏时的最大主应力，kPa。

胡安峰等[33]通过引入循环折减系数λ(式(13))上述砂土模量的弱化效应嵌入到双曲线p-y曲线中，通过与试验结果、数值结果的对比，验证了该循环弱化方法的正确性。

(13)

式中：kxiN为循环荷载作用N次后的水平地基刚度；t为循环荷载下的土体刚度弱化因子。

循环弱化因子t与土体的循环特性、应力状态密切相关，其计算公式为

t=0.251a(X)b

(14)

(15)

(16)

(17)

式中：a，b的取值与式(11)是一致的；p1为静力p-y曲线计算的桩周土反力；Kp为土体的被动土压力系数；γ为土体有效重度；z为土体深度；D为桩径。

根据式(13)～式(17)计算得到N次循环后的土体初始地基刚度kiniN，替换刚度矩阵K中的地基刚度部分，得考虑地基刚度弱化的整体刚度矩阵，代入式(1)，进行求解，得到单桩式海上风机结构的自振频率f0和N次循环后的自振频率fN，该方法计算流程图，如图4所示。

图4 计算原理流程图Fig.4 Flow chart of calculation principle

基于MATLAB数值计算软件平台，将上述理论公式，按照图4的计算流程编写计算程序，下面开展工程应用和对比研究，探讨建立的算法的正确性。

2 工程应用与算法的验证

本文计算方法以爱尔兰Walney风电场单桩式3.6 MW海上风机为例，开展计算结果与现场监测结果、数值计算结果的对比研究，说明建立的简化方法的有效性。

2.1 与工程监测结果的对比

该风机场地条件主要为密实砂土场地，砂土内摩擦角为40°，弹性模量为196 MPa，土体重度为21 kN·m-3[34]。该风机的具体参数如下：风机轮毂高度为83.5 m；本文研究对象为海上风机结构的自振频率，因此将风机和扇叶等结构简化为236 t的集中质量；单桩基础桩径为6 m，埋深为23.5 m；上述塔筒等结构密度为8 500 kg/m3，单桩密度为7 800 kg/m3，弹性模量均为210 GPa。具体尺寸参数如图5所示。

图5 Walney海上风机支撑结构尺寸Fig.5 Diagram of geometry for Walney offshore wind turbine support structures

同时根据规范推荐的模态分析法，基于FLAC3D有限差分平台，建立单桩式海上风机结构整体数值计算模型，如图6所示，地基大小为100 m×100 m×50 m，土体采用弹性本构模型模拟，本研究主要关注桩-土相互作用及场地土特性变化对结构频率的影响，因而单桩、塔筒、轮毂等均采用弹性本构模拟，仅考虑了结构的阻尼比取2%，未考虑风机运行中的气动阻尼等阻尼特性的影响。此外，依据图2确定建立简化方法的土体参数，保证与数值计算模型的土体参数是相互对应的。下面开展在考虑(SPI)与未考虑(No-SPI)桩-土相互作用时，本文建立的计算方法的计算结果与数值计算结果、现场监测结果的对比，如表1所示。

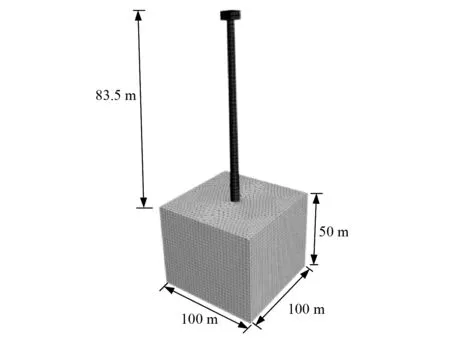
图6 海上风机结构整体数值模型Fig.6 Overall numerical model for offshore wind turbine structure

表1 海上风机结构自振频率计算结果的对比Tab.1 Comparison of natural frequency for offshore wind turbine structure 单位：Hz

由表1的结果对比可知，当考虑桩-土相互作用(SPI)时，本文建立的计算方法的计算结果与试验结果、数值结果的误差在1.5%以内，此外本文建立的方法计算结果较杨春宝等的方法更为接近测量值，同时当塔筒底部固定即未考虑桩-土相互作用(No-SPI)时，本文方法计算值与数值模拟计算结果差异在1%内。综上所述，说明了本文建立的海上风机结构自振频率计算方法的有效性。

2.2 考虑砂土刚度衰减的计算结果对比

下面采用数值模拟计算循环荷载下前述3.6 MW风机的自振频率，并与建立的简化计算方法进行对比，探讨建立的简化方法的合理性。

基于Flac3D内嵌的Fish语言和Achmus等的研究，进行二次开发，在Flac3D数值计算程序实现了砂土的刚度衰减模型，以反映循环荷载对场地土的物理力学特性的影响，其实现过程具体如下：

(18)

(3) 将Xc替换式(11)中的X，根据土体的初始弹性模量，可计算得到N次循环后的土体模量；基于Flac3D内置编程语言，将上述计算流程嵌入到数值模型中，可用于计算N次循环后大直径单桩的受力特性。

采用该数值模型，与张纪蒙等[35]开展的模型试验进行对比，桩基仍采用弹性本构模型，土体采用Mohr-Coulomb弹塑性本构模型，原型桩基桩径为3 m，埋深30 m，土体相对密实度为53%，内摩擦角为33°，弹性模量取值采用式(19)计算。如图7所示，数值计算结果与试验结果基本吻合，说明该土体刚度衰减模型较好地反映了循环荷载下土体的循环弱化特性。

图7 数值计算与试验结果的对比Fig.7 Comparison of numerical calculation and results for tests

(19)

σ3=K0γz

(20)

式中：E0为土体的初始弹性模量，kPa；k′与λ由土体的土体密实程度决定，在此取为380和0.63；σ3为土体的小主应力，kPa；σat为参照应力取大气压力(105kPa)；z为土体深度，m；K0为土体的静止土压力系数。

将该土体刚度衰减模型应用于图6中的数值计算模型中，采用自由振动衰减法计算自振频率，即在塔顶施加一定的荷载，随后将该荷载释放，得塔顶结构的响应时程，然后将该时程进行快速傅里叶变换处理，得其自振频率。

为保证两种方法施加的荷载是一致的，根据式(21)对施加的荷载进行无量纲处理。在数值模型中计算极限水平荷载，然后根据式(21)计算荷载无量纲系数，上述施加的水平位移荷载的无量纲系数ξL为0.17。

(21)

式中：ξL为循环荷载大小的无量纲系数；Smax为循环位移荷载下桩基泥面处的循环水平位移幅值，m；Su为桩基泥面处的极限水平位移，m，大小为0.1D[36-37]。

基于编写的MATLAB计算程序，计算该荷载下桩基不同深度处的桩基水平位移，根据桩基水平位移计算不同深度处的桩基土抗力p1，代入式(15)得到循环应力比X，从而计算N循环后的海上风机结构自振频率。图8是本文算法的计算结果与数值结果的对比，为了清晰地对比两者的差异，横坐标取加载次数的对数。结果表明，两者的计算结果基本一致，均为随着加载次数的增加，自振频率减小，且两者的数值差异在4%，说明了本文建立算法的可行性。

图8 不同加载次数下风机整体自振频率的对比Fig.8 Comparison of natural frequency under different cyclic number

3 参数影响分析

基于上述建立的海上风机结构自振频率简化计算方法，分析循环荷载大小、加载次数、桩径对整体结构系统自振频率的影响规律。

3.1 循环荷载大小的影响

桩基的累积变形发展，属于桩基的疲劳极限状态，所以式(21)中的荷载无量纲系数ξL最大约取0.30。采用本文建立的算法计算不同荷载幅值下的海上风机结构整体自振频率，如图9所示。由图9可知，无论密实场地还是中密场地，随着循环荷载幅值的增大，风机结构系统整体自振频率线性减小，这是由于荷载的增大，桩附近土体的土抗力增大，使得特征循环应力增大，从而导致地基割线刚度衰减程度增大，即刚度矩阵中的地基刚度减小，因而导致风机结构系统自振周期延长。

图9 不同加载次数下风机整体自振频率的对比Fig.9 Comparison of natural frequency under different cyclic number

3.2 加载次数的影响

下面开展循环荷载加载次数对海上风机整体自振频率的影响规律，计算了密实场地、中密场地两类场地中，循环荷载的荷载无量纲系数为0.05～0.25时不同作用次数下风机结构系统的自振频率，由于海上风机结构在其设计周期内承受108循环荷载的作用，因此本文计算中循环荷载次数取108，为了更好地分析循环荷载次数对风机结构整体自振频率的影响规律，取前106的结果，如图10所示。由图10可知，循环荷载加载初期，随着加载次数的增大，结构系统整体自振频率变小；随后当循环荷载次数N大于某一数值时，循环荷载作用次数对风机整体结构自振频率影响较小。由式(11)可知，这是由于循环荷载作用次数的增多，桩周土体的割线模量减小，因而风机结构整体自振频率变小。

图10 不同加载次数下风机整体自振频率Fig.10 Natural frequency of overall structures under different cyclic number

3.3 桩径的影响

下面探讨桩基桩径对海上风机结构系统整体自振频率的影响规律，如图11所示。由图11可知，随着桩基直径从2 m增大到10 m，中密和密实两类场地下风机结构自振频率分别从0.269 Hz增大到0.348 Hz、从0.286 Hz增大到0.353 Hz。结果表明，随着桩基桩径的增大，风机结构系统自振频率对桩径的敏感性减弱；在桩径较小时，桩径的变化对风机结构系统自振频率影响显著，但当桩基桩径较大时(D>5 m)时，桩径的变化对整体结构自振频率影响较小，频率变化在3%以内。因此在单桩式海上风机结构自振频率设计时，应分析桩径的影响，保证桩基直径处于无影响范围内。

图11 不同桩径下风机整体自振频率Fig.11 Natural frequency of overall structure under different pile diameter

4 结 论

为研究长期循环荷载对海上风机结构自振频率的影响，本文基于MATLAB数值分析计算平台，采用结构的动力运动方程，在考虑长期循环荷载对地基刚度影响的基础上，建立了单桩式海上风机结构的自振频率的计算方法，通过与现场监测数据、数值计算结果对比，说明了建立的方法的可行性。最后探讨了循环荷载大小、作用次数、桩径对风机结构自振频率的影响规律。得出如下结论：

(1) 在海上风机结构的疲劳荷载工况下，海上风机结构体系自振频率随着循环荷载幅值的增大而线性减小。

(2) 循环荷载作用初期，风机结构体系自振频率随着循环荷载次数的增大而显著减小；此后其自振频率减小趋势变缓，最终基本稳定而不再随加载次数的增加而变化。

(3) 单桩基础桩径较小时，对风机结构整体自振频率影响显著，存在一界值，当桩基直径大于该数值时，桩基直径的变化对风机结构整体自振频率基本无影响。

(4) 考虑到长期循环荷载作用对风机结构自振频率的降频效应，为保证海上风机结构体系的长期运营安全，结构体系的设计自振频率应稍偏移3P。

(5) 在缺乏风机结构体系自振频率长期监测数据的情况下，本文提出的自振频率简化计算方法可以为单桩式海上风机结构的频率设计提供一定的参考。

本文建立的算法考虑场地条件为均质中密砂土、密实砂土，对于其他密实程度的砂土场地、复杂多层场地、黏土场地下，海上风机结构自振频率在长期循环荷载下的变化规律仍需进一步开展研究。