具有位移放大功能的摩擦自复位支撑及其在双柱式桥墩中的应用

王德斌， 何 杰， 孙治国， 王东升

(1. 大连交通大学 土木工程学院，辽宁 大连 116028； 2. 中国地震局 防灾科技学院 建筑物破坏机理与防御重点实验室，北京 101601； 3. 河北工业大学 土木与交通学院，天津 300401)

已有自复位结构，往往采用预应力筋、组合碟簧、环簧、形状记忆合金等材料作为复位系统，将其与摩擦、金属、黏弹性、磁流变等耗能组件并联完成结构的可恢复功能。然而，自复位结构存在诸多不容忽视的实际问题。首先，现有自复位支撑相比传统支撑，往往耗能不足产生更大的峰值位移，进而对结构管道、外立面等变形敏感部位产生严重影响[1]。其次，低强度地震作用下，耗能组件仅提供抗侧刚度，难以充分发挥其耗能性能[2-3]。再次，现有自复位支撑构造复杂，张拉、预压施工工序繁琐，且经历强震后性能退化，需要及时更换受损耗能元件。

针对上述不足，国内外学者利用肘节机构[4-5]、杠杆机构[6-7]等放大原理，提出了多种位移放大型阻尼器。Shi等[8]将肘撑式BRB耗能装置应用于双柱式桥墩，探讨了该装置的位移放大系数、钢芯长等关键参数对支撑抗震性能的影响，结果表明该支撑布置形式能够充分发挥BRB的耗能能力，有效提升双柱式桥墩的抗震性能。Pavia等[9]采用剪刀型放大机构，将黏滞阻尼器应用于古建筑石塔的减震加固，数值计算结果表明，该方法显著降低了石塔结构的层间位移角及各楼层的峰值加速度，阻尼器耗能能力得到明显提高。Li等[10]基于杠杆原理提出了一种新型旋转放大式黏弹性节点阻尼器，通过放大节点的变形，充分发挥了阻尼器的耗能能力，取得了较为理想的减震控制效果。但以上位移放大装置往往缺少自复位能力，难以有效降低结构的残余变形。

自复位耗能支撑在双柱式桥墩横向减震中的研究结果表明[11-12]，附加自复位耗能支撑的双柱式桥墩，在地震作用下能够有效降低甚至消除墩身残余位移，显著提高桥梁结构的自复位性能。Xue等[13]提出了一种自复位摩擦耗能支撑(self-centering slip friction,SCSF)，阐述了支撑的基本构造和工作机理，研究了初始预压力、摩擦面倾角等关键参数对支撑力学性能的影响，将其应用于双柱式桥墩结构，结构的自复位能力得到明显提高。Dong等[14]对布置自复位支撑(self-centering energy dissipation brace,SCEB)的双柱式桥墩结构进行拟静力低周往复加载试验，结果表明，桥墩残余变形明显降低，结构耗能能力也有所提高。然而，以上自复位支撑均是以降低支撑的耗能为代价，虽然提高了结构的自复位能力，但其自身的耗能均有不同程度减少[15]。

基于上述分析，本文将自复位耗能支撑的可恢复性能和放大阻尼器的高效耗能性能相结合，基于机械领域中的桥式机构放大原理提出了一种具有位移放大功能的扭转摩擦自复位支撑(self-centering displacement amplified rotational friction brace,SC-DARFB)，该支撑将组合碟簧的复位性能和金属材料的摩擦耗能机制相结合。首先，介绍了其具体构造和工作机理，推导了其恢复力模型计算公式，给出了不同角度下转动位移响应放大计算公式。然后，建立了支撑的数值模型并将理论恢复力模型与数值模拟结果进行对比。最后，基于OpenSees软件平台，对附加SC-DARFB支撑的双柱式桥墩进行非线性动力时程分析，验证了SC-DARFB支撑应用于双柱式桥墩结构的可行性和有效性。

1 位移放大型扭转摩擦自复位支撑的构造及工作机理

1.1 SC-DARFB支撑构造

SC-DARFB支撑构造形式如图1所示，该支撑由位于中轴线上的支撑导向系统和环向均匀布置的具有扭转位移放大功能的复位耗能系统两部分组成。该支撑的复位系统和耗能系统属于一体构件，无需额外提供耗能单元，结构形式简单。复位耗能系统可在工厂加工并完成初始预压力的施加，避免了施工现场复杂的预加载、焊接工序。同时，该支撑能够在主体结构正常使用的情况下完成震后受损部件的更换。

图1 SC-DARFB支撑构造Fig.1 Configuration of SC-DARFB brace

SC-DARFB支撑导向系统由具有矩形截面的支撑导向内管和支撑导向外管组成如图2(a)所示，支撑导向内管的外壁边长与支撑导向外管的槽孔边长尺寸相同，以此确保支撑导向内管可在导向外管内自由滑动，且运动方向始终沿支撑中轴线保持不变。复位耗能装置则通过转动摩擦板与固结于内、外支撑导向管外壁的耳板铰接，转动摩擦板可绕耳板在其平面内自由转动。

复位耗能系统采用桥式机构放大原理进行设计，核心组件由转动摩擦板、约束摩擦板、预压销轴和组合碟簧组成，组合碟簧沿两转动摩擦板厚度方向对称布置，如图2(b)所示。转动摩擦板通过端部设置的多个倾斜挤压摩擦面与约束摩擦板端部设置的多个互补挤压摩擦倾斜面无缝隙贴合。由于SC-DARFB支撑复位、耗能系统于一体，耗能系统无需复位力即可完成复位，即在零初始预压力下可完全复位，支撑所设全部初始预压力均提供给主体结构进行复位。

图2 导向系统与耗能系统示意图Fig.2 Schematic diagram of guidance system and energy dissipation system

1.2 SC-DARFB支撑工作机理

SC-DARFB支撑受载前，可根据设计需要对组合碟簧施加初始预压力Fbolt,pr0，增大初始预压力可提高支撑为结构提供的复位力，有利于降低结构主体构件的残余变形。当支撑受载时，支撑导向内管在支撑导向外管槽孔内发生相对运动，通过支撑外壁耳板带动复位耗能系统的转动摩擦板绕预压销轴发生转动，而约束摩擦板两轴孔受到预压销轴的限制作用，使约束摩擦板仅发生垂直于支撑轴线方向的平动，转动摩擦板运动过程中使其内挤压摩擦倾斜面与约束摩擦板的外挤压摩擦倾斜面相互挤压进行摩擦耗能。组合碟簧在加载过程中压缩变形逐渐增大，法向压力也随之增强，促使两摩擦面间的摩擦力矩不断增加。卸载过程中，组合碟簧压缩变形逐渐减小并恢复至初始平衡位置，法向压力随之降低，进而使两摩擦面间的摩擦力矩逐渐减小。在无初始预压力的情况下，恢复至初始平衡状态时，摩擦力为0。

SC-DARFB支撑的单组复位耗能系统工作原理，如图3所示。图3中：F为支撑所受轴向荷载；δ为支撑轴向位移；α0为初始放大角度；Δα为桥式机构放大角度改变量；α为受载后的支撑放大角度；φ为两摩擦面间的相对转角；L为转动摩擦板的有效长度。由图3可知，支撑放大角度与加载位移之间存在如下几何关系

图3 SC-DARFB支撑工作机理Fig.3 Working mechanism of SC-DARFB brace

(1)

(2)

则

(3)

(4)

加载过程中，导向系统环向共对称布置4组复位耗能系统，每组复位耗能系统包含左右对称布置的4对摩擦面。因此，支撑荷载F与单组摩擦面产生的力矩M存在如下关系

(5)

通过上述分析可知，放大角度α在受拉条件下减小，两摩擦面间的相对转动位移放大倍数随之增大；α在受压条件下增大，此时两摩擦面间的相对转动位移放大倍数则有所减小。因此，SC-DARFB支撑产生的荷载-位移曲线存在一定程度的非对称性。由式(4)可知，支撑转动摩擦板长度L直接影响支撑放大系数的变化幅度，其长度过小则直接造成放大角度急剧变化，进而使支撑荷载-位移曲线非对称性明显，易导致最大拉压荷载的比值超过美国钢结构协会规定限值1.3[16]。因此，设计过程中需要注意转动摩擦板的长度L不宜过小，以便确保加载过程中最大拉压荷载比满足规范要求。

2 SC-DARFB支撑的恢复力模型

复位耗能系统通过预压碟簧提供初始预压力，确保约束摩擦板和转动摩擦板发生相对转动进行摩擦耗能，图4给出了摩擦板的具体尺寸参数详图。由图4中可知，摩擦板俯视投影是8个φ=45°具有弧形特征的平面所构成，由此可知摩擦板的最大旋转角度为45°，为避免旋转角度超过45°造成摩擦槽产生跳跃行为，组合碟簧最大设计压缩量应低于摩擦倾斜面两端的高度差h。SC-DARFB支撑耗能系统的滑动面为平面且具有可变的倾斜角θ，该倾斜角θ由内向外逐渐减小(θin>θout)，θout取值为18.25°。

图4 支撑摩擦组件详图Fig.4 Detail view of brace friction assembly

两摩擦板产生的转动力矩为各组摩擦倾斜面绕其中心的转动力矩之和，由于各组摩擦面的摩擦因数、倾斜角度等参数均相同，因此转动过程中各组摩擦面具有相同的转动力矩。当支撑受载时，转动力矩克服摩擦阻力产生的力矩时，即发生旋转滑动。依据文献[17]可知起滑力矩Mslip和恢复力矩Mrestored可由式(6)和式(7)表示

(6)

(7)

式中：Fbolt,pr为组合碟簧预压力；μs，μk分别为加卸载摩擦因数，其值均取为0.15；r为摩擦面上任意一点到圆心的距离。

单组复位耗能系统各关键加、卸载点的部件变形情况，如图5所示。复位耗能系统加载过程中的极限力矩Mult和极限卸载力矩Mrestoring通过改变加卸载公式中的预压力Fbolt,pr进行计算，最终得到单组耗能系统摩擦力矩M与转角φ的关系曲线，如图6所示。加载过程中，随着支撑位移的增加，组合碟簧将被进一步压缩，其压缩变形Δ可通过式(8)进行计算

图5 复位耗能系统加载过程Fig.5 Self-centering and energy dissipation system loading process

图6 摩擦力矩-转角理论恢复力模型Fig.6 Theoretical restoring force model of friction torque-angle

(8)

支撑受载过程中，组合碟簧的预压力可由式(9)计算

(9)

式中，k为组合碟簧刚度，本文采用内径41 mm、外径80 mm的A系列碟簧，其布置方式采用单层对合，初始预压力Fbolt,pr0=12 kN，刚度k=438.8 kN/m。

3 有限元模型的建立和验证

3.1 有限元模型的建立

基于前述理论给出的恢复力模型，设计支撑关键部件尺寸参数如表1所示，各参数的具体含义见图4。通过理论计算可知其满足美国钢结构协会规定的最大拉压荷载比限值1.3。本文共选取三种初始放大角度α0进行支撑力学性能分析，α0=45°作为对照组，此时支撑位移无放大，选取α0=37.5°和α0=30°作为支撑位移放大组，编号分别为SC-DARFB-1，SC-DARFB-2和SC-DARFB-3，研究SC-DARFB支撑在不同放大倍数下力学性能的总体变化规律。

表1 支撑关键部件尺寸参数值Tab.1 Dimension parameter value of key brace components

基于ABAQUS有限元软件建立SC-DARFB支撑计算模型，如图7所示。支撑各部件均采用八节点线性六面体减缩积分实体单元(C3D8R)。转动摩擦板与约束摩擦板之间法向采用“硬接触”，切向接触采用“罚函数”摩擦进行模拟，摩擦因数取为0.15。采用Hinge连接单元模拟各部件之间的转动行为，组合碟簧采用Connector连接器进行模拟，基于设计的预压力计算得到组合碟簧的初始压缩量，进而通过设置参考长度反应其初始预压力。

图7 SC-DARFB支撑有限元模型Fig.7 Finite element model of SC-DARFB brace

转动摩擦板与约束摩擦板网格进行细化以帮助收敛和提高结果的准确性，其单元尺寸为5 mm，其余部件单元尺寸为50 mm。转动摩擦板和约束摩擦板均选用Q345级钢，屈服强度为fy=345 MPa，抗拉强度为fu=500 MPa，弹性模量为E=206 GPa，泊松比为ν=

0.3，其余构件均采用Q690高强钢，所有材料均采用双线性随动强化模型。支撑两端面设立参考点RF分别与两端面运动耦合，采用位移控制加载模式对参考点进行低周往复加载。初始加载位移为2.5 mm，后续加载位移均采用2.5的整数倍进行逐级加载，直至位移加载至15 mm，结束加载。

3.2 恢复力模型验证

基于前文理论计算得出的SC-DARFB支撑各阶段的荷载-位移曲线与数值模拟结果对比，如图8所示。由于起滑位移较小，此时拉、压荷载下支撑放大角度α并无明显变化。基于此，表2仅列出支撑受拉时的起滑荷载。取位移加载至15 mm时对应荷载为最大荷载值，受拉条件下，支撑放大角度α逐渐减小，由式(5)可知，此时支撑放大倍数相较于初始放大角度α0进一步增加，而受压时则有所减小。鉴于拉、压条件下荷载放大系数的反向变化特点，最大拉、压荷载值均在表2中列出。

图8 理论预测与数值模拟结果对比Fig.8 Comparison between theoretical prediction and numerical simulation results

表2 SC-DARFB主要计算结果Tab.2 Main calculation reults of SC-DARFB

从表2和图8可以看出，通过理论计算得到的支撑起滑荷载和最大拉、压荷载基本一致，误差均在5%以内，滞回曲线理论值与数值模拟结果吻合度较高，但两者加卸载刚度误差较大。其原因主要是：①理论计算过程中并未考虑刚度的变化，而是直接基于不同加载阶段的位移值通过理论公式计算获取支撑荷载值；②有限元分析过程中，各传力单元之间存在一定程度的局部变形，且不同参数条件下局部变形不尽相同，导致支撑变形偏大，即总体刚度偏小[18]。可见，支撑恢复力模型基本能够准确预测数值模拟结果。

3.3 SC-DARFB支撑滞回性能对比

数值模拟得到的SC-DARFB支撑在各初始放大角度α0下的滞回曲线，如图9所示。从图9中可知，支撑滞回曲线具有显著的旗帜型特征，滞回曲线饱满，具有较好的耗能能力，但滞回曲线具有明显的非对称特征。各加载阶段结束后，支撑均能实现完全复位，并无明显残余变形。依据前述理论分析可知，随着初始放大角度α0的减小，两摩擦板间的相对转角φ逐渐增大，促使组合碟簧的压缩变形量增加，进而增大了耗能系统的摩擦力矩，则支撑轴向产生的水平分力成倍增加。结合图9可以看出，与初始放大角度α0=45°的支撑SC-DARFB-1相比，支撑SC-DARFB-2和SC-DARFB-3在不同加载阶段的荷载值均显著提高，两支撑的起滑荷载分别提高15.1%和44.0%，最大受拉荷载分别提高18.3%和48.1%，最大受压荷载分别提高15.6%和39.1%。图10给出了不同初始放大角度α0下的支撑累计耗能，可以看出随着支撑初始放大角度的α0的减小，支撑耗能能力明显提高。相较于支撑SC-DARFB-1，SC-DARFB-2和SC-DARFB-3的总耗能分别提高19.6%和45.7%。可见，本文提出的SC-DARFB支撑随着初始放大角度α0的减小能够有效提高结构的承载力需求，具有显著的自复位能力，并有利于增强支撑的总体耗能。

图9 数值模拟结果对比Fig.9 Comparison of numerical simulation results

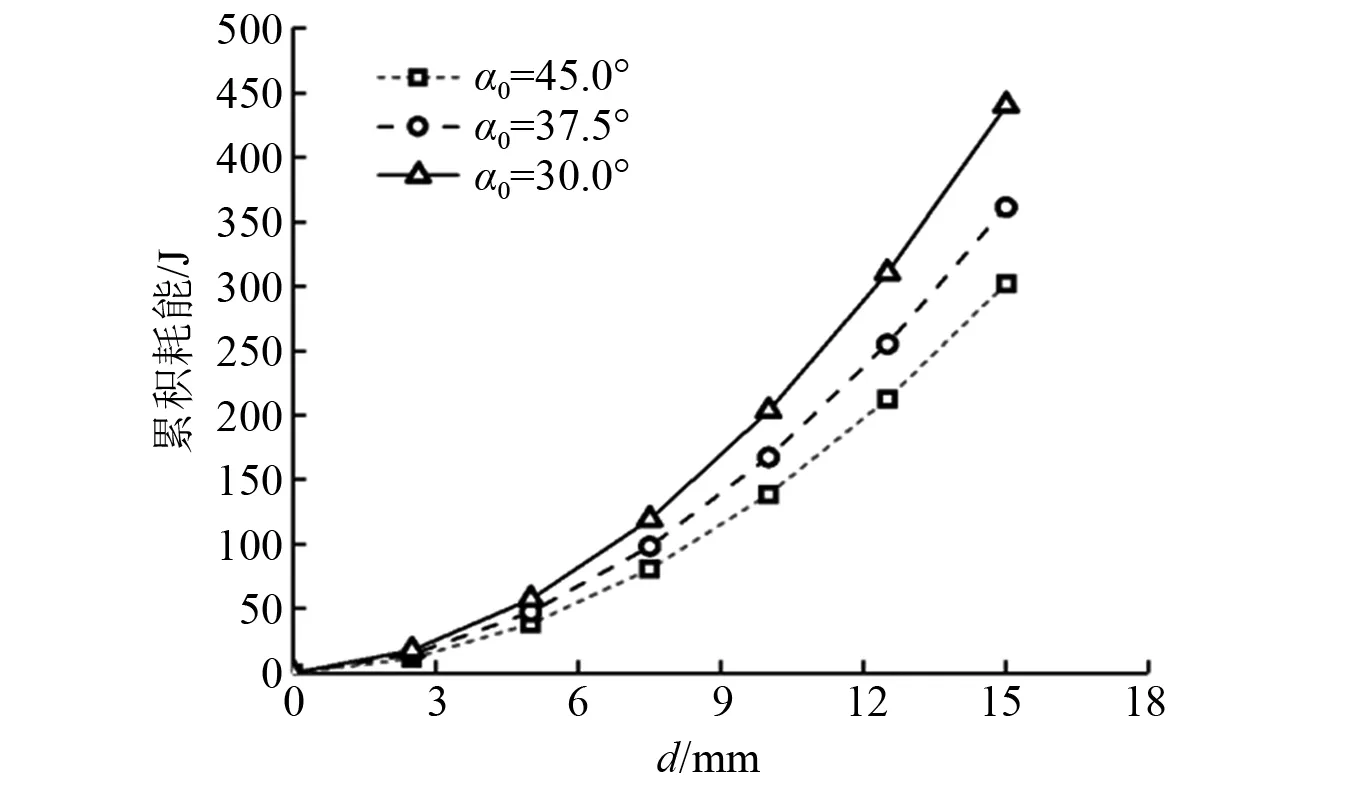
图10 累计耗能对比Fig.10 Comparison of cumulative energy consumption

表2给出了支撑在不同初始放大角度α0下的最大拉压荷载比，由于支撑受拉时，α会随位移幅值的增大而减小，受压时则随之增大。以位移加载至15 mm为例，支撑SC-DARFB-2和SC-DARFB-3实际放大角度α分别为36.16°和28.43°，而受压时实际放大角度α分别为38.84°和31.57°。因此，滞回曲线展现出一定的非对称特征。α0初设角度越大，支撑转动摩擦板与约束摩擦板相对转动位移越小，α0=45.0°时支撑SC-DARFB-1内外摩擦板相对转动位移无放大，此时拉压最大荷载比接近1，但仍然受到加载过程中α值的变化展现出轻微的非对称性，此时拉压最大荷载比为1.043。α0=30.0°时，支撑SC-DARFB-3非对称性特征最为明显，其拉压最大荷载比为1.113，仍低于美国钢结构协会规定限值1.3，满足支撑结构的抗震性能需求。需要指出的是，由于SC-DARFB支撑滞回曲线的非对称性特征，建议进行抗震设计时采用倒V型对称布置形式。

4 设置SC-DARFB支撑双柱式桥墩减震性能研究

4.1 支撑双柱式桥墩模型建立

双柱式桥墩作为主要承重构件在桥梁结构中得到广泛应用，已有研究主要采用摇摆墩实现其自复位性能[19]，而采用自复位支撑对桥墩结构进行复位的相关研究仍然非常有限。本文选取文献[20]中的规则双柱式桥墩结构，将提出的SC-DARFB支撑附加于该桥墩结构，其结构模型及计算简化模型如图11所示。基于OpenSees软件建立双柱式桥墩计算模型，盖梁采用线弹性梁单元模拟，桥墩采用具有纤维截面的非线性梁单元模拟，钢筋、混凝土分别采用Steel02和Concrete01材料模型，BRB采用Truss单元模拟，防屈曲支撑本构模型采用Steel02材料本构。由于SC-DARFB支撑具有明显的非对称特征，而OpenSees材料库并无非对称旗帜型材料本构模型，本文将材料Elastic-No Tension Material和ElasticBilin Material进行并联获取SC-DARFB支撑的非对称特征数据，并将其与Self-Centering材料再次进行并联得到SC-DARFB支撑本构模型，其获取过程如图12所示。

图11 附加SC-DARFB支撑双柱式桥墩模型Fig.11 The analysis model of double column bridge bents with SC-DARFB brace

图12 SC-DARFB材料本构模型建立流程图Fig.12 Flow chart of SC-DARFB material constitutive model

选取7组近场地震动记录进行动力时程分析，其加速度反应谱如图13所示，具体信息见参考文献[21]。动力时程分析时沿横向输入地震动，峰值加速度分别取为0.2g，0.4g和0.6g分别代表中震、大震和巨震，并取各地震动结构响应峰值的平均值作为分析依据。为研究BRB和SC-DARFB支撑的减震效果差异及初始放大角度α0对SC-DARFB支撑减震性能的影响，共设计4种分析工况，均采用倒V型支撑布置形式。工况1采用BRB支撑，其屈服荷载为500 kN，初始刚度为2.0×105kN/m，屈服后刚度为初始刚度的1%。工况2～工况4均采用SC-DARFB位移放大型支撑，初始放大角度α0分别取为45.0°，37.5°和30.0°，工况2中SC-DARFB与BRB 两者采用等屈服力设计原则，可通过前文理论模型计算获取，本文取SC-DARFB起滑荷载作为支撑屈服荷载，工况3和工况4则通过调整工况2中SC-DARFB初始放大角度α0进行设计。

图13 地震动加速度反应谱Fig.13 Acceleration spectrum of ground motions

4.2 设置SC-DARFB双柱式桥墩墩顶位移对比

图14给出了不同工况下桥墩墩顶最大位移响应均值。从图14中可知，SC-DARFB支撑相较于BRB具有更佳的减震效果。SC-DARFB支撑初始放大角度α0=45.0°时，中震和大震作用下采用BRB的桥墩墩顶位移均高于采用SC-DARFB支撑的桥墩结构，但在巨震作用下位移响应最大值呈现出相反的特征，其主要原因是低强度地震作用下，结构对支撑的耗能需求较低，同时SC-DARFB支撑初始刚度较高增大了桥墩对盖梁横向弹性约束作用，导致其具有更好的减震效果，而当PGA为0.6g时，SC-DARFB与BRB屈服承载力相同的情况下，结构进入明显的非线性阶段，耗能需求也随之增加，而SC-DARFB的耗能能力较弱，导致自复位结构的墩顶峰值位移较大。

图14 双柱式桥墩墩顶最大位移平均值Fig.14 Average maximum displacement at the top of the double column bridge bents

不论中震、大震还是巨震作用下，采用SC-DARFB的桥墩墩顶位移均随支撑初始放大角度α0减小而减小，基于前述理论分析可知α0减小会提高SC-DARFB支撑的承载力，同等位移条件下其包围的面积也随之增大，进而提高了支撑的减震、耗能能力。图15给出了编号为RSN723的地震波作用下的双柱式桥墩结构的墩顶位移时程曲线，表3给出了不同工况下双柱式桥墩墩顶最大位移值及不同初始放大角度α0下SC-DARFB支撑相较于BRB的墩顶位移减震率。结合表3和图15可以看出，相较于BRB支撑，SC-DARFB支撑展现出更佳的减震性能，其初始放大角度对支撑的减震性能具有决定性作用。

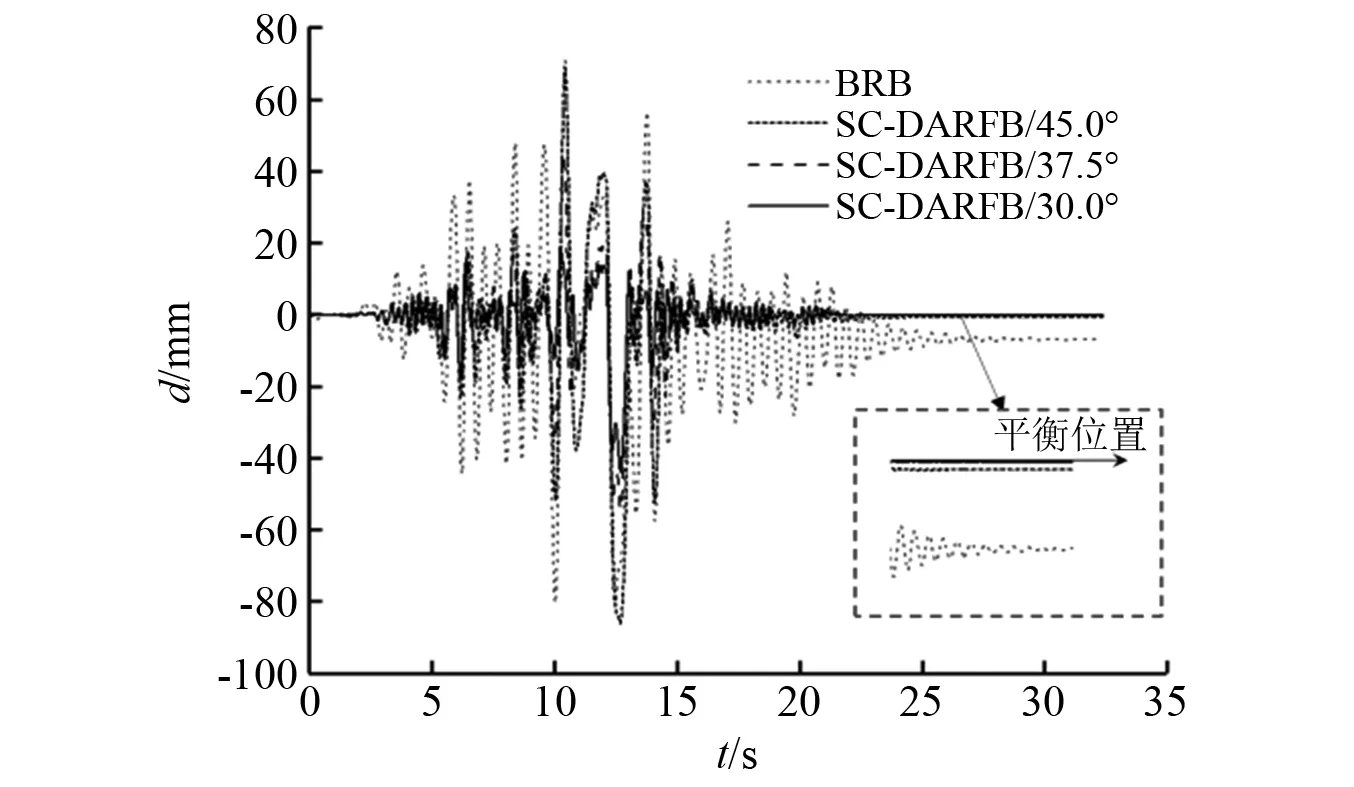
图15 RSN723地震作用下墩顶位移Fig.15 Displacement at the top of the pier under RSN723 ground motion

表3 不同工况下桥墩墩顶最大位移Tab.3 Maximum displacement of pier top under different working conditions

4.3 设置SC-DARFB支撑双柱式桥墩残余位移角对比

桥梁结构在强震作用下产生过大残余变形是导致结构破坏的主要原因，也是衡量桥墩可修复性能的重要指标，日本(1996年)提出的桥梁规范规定桥墩抗震设计残余位移角限值为1%。图16给出了不同支撑下桥墩在7条地震波作用下最大残余位移角的平均值。

图16 桥墩残余位移角Fig.16 The residual drift ratio of pier

由图16中可知，随着地震动强度的提高，各工况下桥墩的残余位移角均有所增加，BRB支撑结构展现出更大的桥墩残余位移角，PGA为0.6g时桥墩残余位移角取得最大值为0.289%，但仍低于1%， 满足日本桥梁抗震规范提出的可恢复性能要求。相比BRB支撑桥墩，SC-DARFB支撑桥墩残余位移角明显降低，PGA在0.2g和0.4g条件下，桥墩基本无残余变形。PGA为0.6g时SC-DARFB支撑初始放大角度α0=45.0°时，桥墩残余位移角为0.014%，与BRB支撑桥墩相比，其最大残余位移角减小95%以上，而初始放大角度α0=37.5°和α0=30.0°时，桥墩最大残余位移角进一步降低，其值仅为0.009 1%和0.005 7%，基本无残余位移。说明强震作用下，SC-DARFB支撑能够有效减小桥墩残余位移，且支撑初始放大角度越小其可恢复性能越明显。

4.4 SC-DARFB支撑滞回性能对比

图17为地震波编号RSN184作用下PGA为0.4g时BRB和不同初始放大角度下SC-DARFB支撑的滞回曲线。从图17(a)可知，BRB在屈服后产生较大的塑性变形，荷载消失后支撑并未恢复至初始平衡位置，存在明显的残余变形。而由图17(b)、图17(c)和图17(d)可知，SC-DARFB支撑在地震作用后由于复位力的存在使支撑能够完全恢复至初始平衡位置，并且能够为结构提供一定的复位力。基于前述理论分析可知，随着SC-DARFB初始放大角度α0的减小，复位耗能系统摩擦面间的相对转动位移也随之增大，产生的摩擦力矩在支撑加载方向的分力也显著提高，即支撑在较低的位移水平下即可完成结构的承载力需求和耗能需求。

图17 不同工况下支撑滞回曲线Fig.17 Hysteretic curves of brace under different working conditions

初始放大角度α0=45.0°时，SC-DARFB支撑最大轴向变形和荷载分别为19.6 mm和501.6 kN，初始放大角度α0=37.5°和α0=30.0°时，支撑最大轴向位移仅为12.9 mm和10.4 mm，轴向荷载分别为554.7 kN和674.7 kN。可见随着初始放大角度的减小，支撑承载能力显著提高，并且能够有效降低结构对支撑的位移需求，进而降低支撑的破坏可能性，提高支撑的使用寿命。

5 结 论

本文提出了一种具有位移放大功能的摩擦自复位支撑，详细介绍了SC-DARFB的基本构造，阐述了其工作机理，给出了支撑的理论恢复力模型。基于ABAQUS软件对其滞回性能进行了数值模拟，验证了恢复力模型的准确性，并对附加SC-DARFB的双柱式桥墩抗震性能进行了动力时程分析。主要结论如下：

(1) 本文基于给出的SC-DARFB支撑理论恢复力模型得到的滞回曲线与ABAQUS软件数值模拟得到的结果基本吻合，验证了本文恢复力模型的准确性和合理性。

(2) 基于桥式放大工作原理提出的SC-DARFB在往复荷载作用下的滞回曲线饱满且具有显著的旗帜型特征，初始放大角度的减小能够提高支撑的起滑荷载、最大荷载和累计耗能等各项力学性能指标。

(3) SC-DARFB随着初始放大角度的减小，滞回曲线非对称特征愈加明显，鉴于此本文提出的SC-DARFB宜采用倒V型布置形式减震耗能效果更佳。

(4) 基于OpenSees平台多次采用并联机制给出了SC-DARFB简化模型构建方法，将其应用于双柱式桥墩结构，能够减小结构的墩顶位移，并极大降低桥墩的残余位移角，有效提高双柱式桥墩结构的抗震性能。