考虑静差消除的混沌电力系统有限时间命令滤波反步控制

李静贤， 王 聪， 张宏立， 张绍华

(新疆大学 电气工程学院，乌鲁木齐 830047)

大规模的电网互联为电力生产和消费带来了巨大的便利，但是其高度复杂化的网络结构以及大量非线性电气设备的接入，会导致电力系统对参数扰动、时间延迟更为敏感[1]。电力系统本身是一个强非线性、强耦合性、多变量的动态系统，具有复杂的非线性动力学行为，更容易引发整个电力系统的剧烈振荡，甚至失稳[2-4]。在实际电力系统中，混沌现象时有发生，导致相角发散、频率振荡和电压崩溃，甚至会导致灾难性的停电[5-7]。因此，采取有效的控制策略对电力系统的混沌振荡现象加以控制，对整个电力系统的安全稳定运行具有重要意义。

近年来，针对电力系统的混沌振荡现象，文献主要集中于动力学行为分析和混沌控制策略研究。文献[8]结合滑模控制原理，提出一种失配扰动观测器的设计方法，有效缓解了电力系统混沌振荡的问题，从而保证电力系统的稳定运行。文献[9]针对六维三母线电力系统，基于李雅普诺夫自适应算法，结合协同控制理论设计控制量，解决了电力系统混沌振荡问题。文献[10]基于LaSalle不变性原理，提出一种自适应控制律，将不稳定的系统渐近稳定到平衡点，从而控制电力系统达到稳定。文献[11]设计了一种基于模糊监督器的滑模控制律，使系统满足Lyapunov稳定，从而抑制系统混沌振荡、消除控制信号颤动。文献[12]针对受控电力系统，定义对应的宏变量，设计具有连续控制律的协同控制输入，从而有效抑制系统的振荡。

以上方法针对电力系统的混沌振荡都表现出较好的控制效果，但是控制量结构复杂，在实际工程中的实现较为困难。采用有限时间稳定原理的控制策略设计更加符合实际工程需求，并且在电力系统混沌控制中的应用较少[13]。文献[14-16]分别针对参数不确定的永磁同步电机、处于振荡状态的机械臂以及串级连续搅拌反应釜系统，采用模糊逻辑对未知的非线性函数进行逼近，加入命令滤波器及误差补偿器对系统控制器进行设计，并证明了系统的有限时间稳定。但上述方法是在系统正常运行状态下进行跟踪控制，未探讨系统处于混沌状态下的控制效果，并且该控制方法仅采用比例反馈律，没有考虑系统跟踪控制过程中产生的静态误差问题。

本文基于以上研究，针对电力系统的混沌现象，提出一种考虑静差消除的有限时间命令滤波反步控制方法。通过径向基神经网络对电力系统中相互耦合的复杂未知非线性项进行逼近，加入命令滤波器及误差补偿器，实现对虚拟控制量的求导及误差补偿；同时，考虑到跟踪过程中的静差问题，引入误差积分反馈律，进一步削弱控制量之间的耦合关系，并达到静差消除的目的；最后，通过反步法得出电力系统的控制律，并推导出系统满足有限时间稳定，使系统输出稳定在期望的轨道上，从而间接实现电力系统的混沌控制。理论推导与仿真试验证明，本文所提的控制方法能够有效抑制电力系统的混沌振荡现象，消除系统静态误差，保证了电力系统的安全稳定运行。

1 三节点四阶电力系统模型

本文将具有可变电压幅度形式的电力系统作为研究对象，其系统模型如图1所示[17-18]。

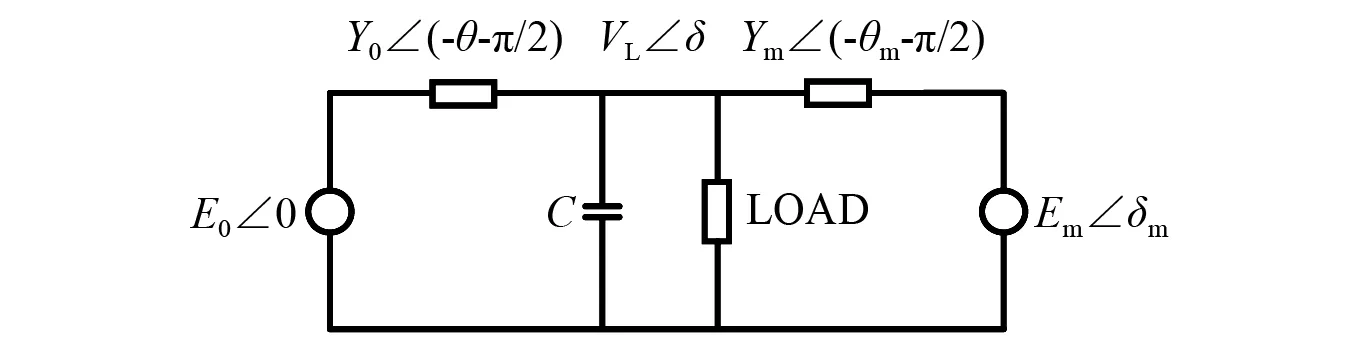
图1 电力系统模型Fig.1 Power system model

系统由电机端和负荷端组成。其中，负荷模型包括并联的恒定PQ负载和动态感应电动机，感应电机需要根据负载电压和频率来指定电动机的有功和无功功率要求。根据图1构建三节点四阶电力系统的动力学模型

(1)

式中：δm为发电机电压相角；ω为电机的角速度；δ为负载电压相角；V为负载电压；P0，Q0分别为电动机的恒定有功功率和无功功率；P1，Q1分别为PQ负荷的有功功率和无功功率；Kpω，Kpv，Kqω，Kqv，Kqv2，T为比例系数。M，dm和Pm分别为发电机的惯性、阻尼和机械功率；η表示为

η=arctan(Kqω/Kpω)

取系统参数如表1所示。

表1 三节点四阶电力系统参数表Tab.1 Three-node fourth-order power system parameter table

系统参数Q1取不同的值时，电力系统呈现出不同的动力学特性。当Q1取值范围为 [11.376 6,11.382 0]时，电力系统处于混沌状态。

图2和图3分别给出了Q1=11.379 0时电力系统的相轨迹和时间响应曲线。图2的相轨迹表现为：局部来看，系统背离平衡点，做无序的振荡运动，处于不稳定状态；全局上来看，系统的相轨迹局限于固定区域内，没有发散至无穷远处。图3给出了电力系统输出的时间响应曲线，其输出均在一定的范围内做无规律的振荡运动，并处于无序状态。因此可以定性得出，电力系统处于混沌振荡的运行状态。

图2 电力系统相轨迹Fig.2 Power system phase trajectory

图3 电力系统各输出时间响应曲线Fig.3 Power system output time response curve

图4给出了Q1=11.379 0时电力系统Lyapunov指数谱，其输出的最大Lyapunov指数分别为：0.243 01，-0.182 02，-5.277 90，-61.681 40，存在最大Lyapunov指数大于零的情况。因此可以定量得出，电力系统处于混沌振荡的运行状态。

图4 电力系统Lyapunov指数谱Fig.4 Power system Lyapunov exponent spectrum

由以上分析可得，电力系统中出现混沌现象时，往往伴随着系统的振荡，甚至引发系统的裂解、崩溃，直接影响电力系统的安全稳定运行。因此，采取适当的控制策略抑制电力系统的混沌振荡现象，对于电力系统的正常稳定运行具有重要的意义。

2 考虑静差消除的混沌电力系统有限时间命令滤波反步控制

根据式(1)，取[δm，ω，δ，V]=[x1，x2，x3，x4]。发电机电压相角δm与并网端电压相角保持相对稳定，对于保证发电机功率传输的稳定性至关重要，一般通过控制发电机组角速度ω来实现发电机电压相角δm的稳定性，故将控制量作用在电机的角速度ω上，实现对发电机电压相角δm的控制。同时，为了保证电力设备的供电安全，需要实现负载电压相角δ的稳定。在阻感性负载下，负荷将产生一定的无功功率，而过多的无功功率会造成电力系统电压V的抬升，甚至越线，通常采用无功补偿设备来实现对电力系统中无功能量的吸收及电压V的调节。因此本文采用将控制量作用在负载电压V上，从而达到对负载电压相角δ的稳定控制。综合功率传输的稳定性及电力设备的供电安全双重因素，考虑在方程组的第二、第四项中分别加入控制量u1和u2，得到如下的受控电力系统模型

(2)

本文的控制目标为：针对三节点四阶电力系统，设计一种具有静差消除的有限时间命令滤波反步控制策略，使得系统的输出x1与x3能够跟踪上期望的轨迹xd1与xd2，让系统的跟踪误差收敛至原点。

假设1f1(X)，f2(X)，f3(X)均为具体形式的连续未知函数，其一阶导数连续有界。

在实际电力系统中，f1(X)，f2(X)，f3(X)均为以电力系统的4个状态变量作为自变量，由常函数、三角函数、指数函数等基本初等函数的有理运算组合而成的初等函数，其一阶导数均满足连续的要求。同时电力系统的4个状态变量均为归一化的标幺值，取值范围均有界，有界函数的有理运算仍为有界函数，因此，f1(X)，f2(X)，f3(X)的一阶导数满足有界性，其具体形式将在下文给出。

假设2 理想轨迹xd1，xd2连续、有界，其一阶导数和二阶导数均连续有界。

引理1 本文采用的二阶命令滤波器，其定义为

(3)

引理2 万能逼近定理：若f(X)为定义在紧密集Ω上的连续函数，则必定存在一个径向基神经网络WTS(X)，使f(X)=WTS(X) +ξ(X)成立。其中W=[w1,w2, …,wn]T为线性加权项，n为神经网络的节点数，S(X)=[p1(X),p2(X), …,pn(X)]T为径向基函数向量。ξ(X)为逼近误差，且满足‖ξ(X)‖≤ε。其中第j个径向基函数表示为

(4)

引理3 杨氏不等式：对于∀(Φ,Ψ)∈R，有

(5)

成立。其中：(p-1)(q-1)=1，p>1，q>1；Θ>0。

引理4 有限时间理论：存在函数V(x)∈C2，χ1，χ2∈K∞，式(2)满足

χ1(‖x‖)≤V(x)≤χ2(‖x‖),
LV(x)≤-μ1V(x)+μ2

(6)

则式(2)在有限时间内稳定。其中，μ1，μ2均大于零。

由于传统的反步法会引入虚拟控制量的各阶导数项，导致计算爆炸的问题[19-21]。本文引入命令滤波器，来逼近虚拟控制律以及其一阶导数项。因此定义系统的跟踪误差为

(7)

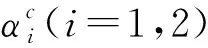
考虑到命令滤波器的加入会产生滤波误差，使滤波器输入输出信号之间产生相位差，影响到系统跟踪性能。因此本文引入误差补偿变量δi(i=1,2)来消除滤波误差对系统产生的影响。定义加入误差补偿后，系统的误差子系统为

(8)

步骤1由上述定义的补偿后误差变量为

r1=e1-δ1

(9)

对式(9)求导可得

(10)

构造Lyapunov函数为

(11)

对其求导可得

(12)

设计虚拟控制率α1和误差补偿变量δ1的导数为

(13)

(14)

式中，k1，k11为参数，且满足k1>0,k11>0。将式(13)和式(14)代入式(12)中得

(15)

步骤2由上述定义的第二个补偿后的误差变量为

r2=e2

(16)

对其进行求导，可得

(17)

构造Lyapunov函数为

(18)

对其进行求导可得

(19)

其中，

(20)

由于变量x1，x2，x3，x4为归一化后的标幺值，均为有界变量，由式(20)可知，f1(X)二阶可导，则f1(X)一阶导数连续且有界。

(21)

且有|ξ1|≤ε1。由引理3可知

(22)

则有

(23)

在这一步中，存在真实的控制律，设计控制律u1为

(24)

式中，k2为参数，且有k2>0。将式(24)代入式(23)得

(25)

步骤3设计x1与x2的Lyapunov函数为

(26)

对式(26)进行求导，可得

(27)

步骤4由上述定义的第三个补偿后的误差变量为

r3=e3-δ2

(28)

对其进行求导，可得

(29)

构造Lyapunov函数为

(30)

对其进行求导，得到

(31)

其中，

(32)

由于变量x1，x2，x3，x4为归一化后的标幺值，均为有界变量，由式(32)可知，f2(X)二阶可导，则f2(X)一阶导数连续且有界。

(33)

且有|ξ2|≤ε2。由引理3可知

(34)

则有

(35)

在这一步中，设计虚拟控制率α2以及误差补偿变量δ2的导数为

(36)

(37)

式中，k3，k22为参数，且满足k3>0,k22>0。将式(36)和式(37)代入式(35)得

(38)

步骤5上述定义的第4个补偿后的误差变量为

r4=e4

(39)

对其进行求导，可得

(40)

构造Lyapunov函数为

(41)

对其进行求导，得到

(42)

其中，

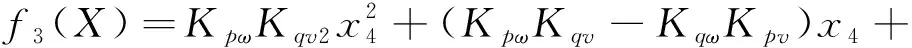
(43)

由于变量x1，x2，x3，x4为归一化后的标幺值，均为有界变量，由式(43)可知，f3(X)二阶可导，则f3(X)一阶导数连续且有界。

(44)

且有|ξ3|≤ε3。由引理3可知

(45)

将式(45)代入式(42)则有

(46)

在这一步中，设计真实的控制率u2为

(47)

将式(47)代入式(46)得

(48)

步骤6设计系统的Lyapunov函数为

(49)

对式(49)进行求导，可得

(50)

3 稳定性证明

设计系统的Lyapunov函数为

(51)

在上述控制律的作用下，可求得Lyapunov函数的导数为

(52)

系统满足

(53)

其中，

μ1=min{2k1,2k2,2k3,2k4}

(54)

(55)

由引理4可知，式(2)在有限时间内收敛至原点。

由于电力系统状态变量之间存在复杂、非线性的耦合关系，当系统参数选取在特定范围时，状态变量呈现振荡且无序的变化状态，导致电力系统不能稳定运行。本文考虑加入外界控制量来打破混沌状态，使电力系统脱离混沌，正常运行。由以上分析可知，在上述控制律的作用下，混沌电力系统能够在有限时间内跟踪期望的稳定轨道，从而脱离混沌状态，实现电力系统的混沌控制。

4 仿真结果分析

为验证本文所设计方法的有效性，搭建三节点四阶电力系统动力学模型，设计如上文所推导的控制律，对本文的方法进行验证。

选取系统参数见表1，同时选取命令滤波器的参数为：ξ=0.5，ωn=200。选取控制量的参数为：k1=100，k2=10，k3=100，k4=10，k11=300，k22=300，h1=1，h2=0.6，h3=0.6。选取系统的跟踪信号为：xd1=0.02，xd2=0.002cos(20t)+0.12。

采用径向基神经网络对电力系统中的三个未知非线性函数f1(X)，f2(X)，f3(X)进行逼近，考虑到逼近时径向基神经元的个数与函数的复杂程度不同，最终其拟合效果如图5所示。

图5 径向基神经网络逼近f1，f2，f3Fig.5 RBF neural network approximates f1, f2, f3

由图5可以得出，采用径向基神经网络可以很好得逼近复杂的非线性函数，其拟合程度较高，其中f1(X)的逼近误差最大值约为±0.02，f2(X)的逼近误差最大值约为±0.015，f3(X)的逼近误差最大值约为±0.016，拟合误差较小，可见采用径向基神经网络逼近方法可以较为精确地还原电力系统中连续未知函数的输入输出特性，为实现混沌电力系统的精确控制提供了基础。

对文中设计的两个虚拟控制信号分别加入命令滤波器及误差补偿器。图6和图7分别给出了加入误差补偿器前后命令滤波器1、2的输出误差情况，命令滤波器的输入为虚拟控制信号，其输出为虚拟控制信号的滤波和导数。由于虚拟控制信号包含检测噪声，采用命令滤波器可以实现对高频噪声的滤除，但会造成虚拟控制信号在幅值和相位上的失真，采用误差补偿器对信号进行补偿，更精确的还原虚拟控制信号及其导数，增加滤波及求导的可靠性。从图6可以得出，命令滤波器1在未加入补偿之前，滤波误差最大值约为0.04，加入补偿变量δ1之后，虚拟控制信号在幅值和相位上的失真进一步减少，滤波误差得到了有效抑制，基本为零；从图7可以得出，命令滤波器2在未加入补偿之前，滤波误差最大值约为0.015，加入补偿变量δ2之后，滤波误差幅值进一步减少，误差曲线更为平滑。可见加入误差补偿器能够有效抑制滤波误差，提高控制量的精确性，从而达到更好的混沌电力系统控制效果。

图6 命令滤波器1误差补偿效果对比Fig.6 Command filter 1 error compensation effect comparison

图7 命令滤波器2误差补偿效果对比Fig.7 Command filter 2 error compensation effect comparison

图8给出了δm，ω，δ，V的初始值分别为0.3，0，0.2，0.97时的电力系统零输入时间响应曲线，电力系统的电机电压相角、电机的角速度、负载电压相角、为、负载电压都呈现为往复的振荡、发散状态，混沌且无序。可见在未对电力系统施加有效控制时，电机电压相角、电机的角速度、负载电压相角和负载电压之间存在深度耦合关系，无法自主脱离混沌状态，处于不稳定运行状态，极易导致电力系统崩溃。

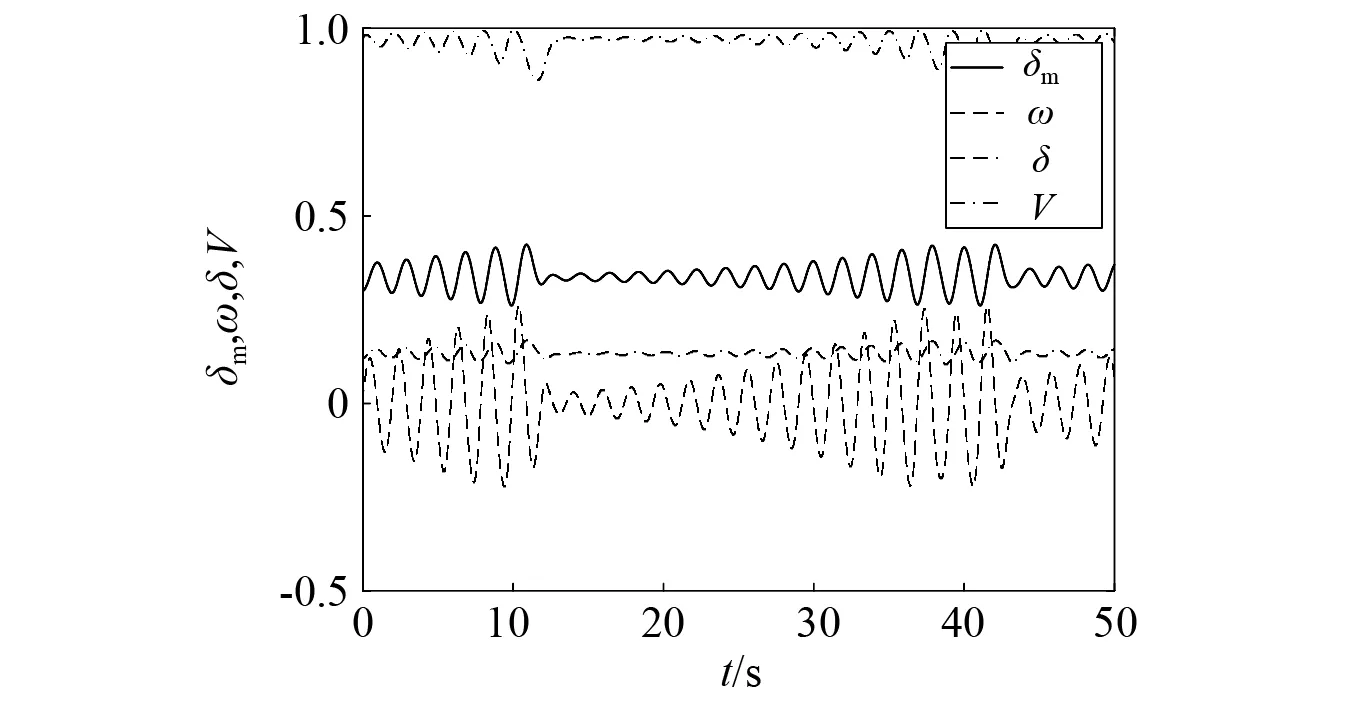
图8 零输入时间响应曲线Fig.8 Zero input time response curve

图9给出了电力系统加入控制量前后的时间响应曲线。在电力系统进入混沌振荡后的20 s处加入控制量u1，在25 s处加入控制量u2。在加入控制量前，各个状态变量处于混沌状态，在控制量u1加入后，系统马上脱离了混沌状态，振荡现象得到了有效抑制，加入控制量u2之后，电力系统仍然处于稳定状态。可见采用考虑静差消除的有限时间命令滤波反步控制方法，能快速的让电力系统脱离混沌振荡状态，保证了电力系统的安全稳定运行。

图9 加入控制量系统时间响应曲线Fig.9 Add the time response curve of the control quantity system

图10和图11分别给出了加入误差积分反馈律前后的电机电压相角δm跟踪效果。加入误差积分反馈律，本质是对误差系统进行升阶，引入误差积分项，当误差系统达到稳定时，误差积分项存在静态误差，而误差项不存在静态误差，因此可以消除混沌系统控制过程中的静态误差。图10和图11可以得出，未加入控制量时，发电机电压相角处于混沌振荡的状态；在20 s处加入控制量u1，电机电压相角迅速响应，电力系统脱离混沌，并与跟踪信号xd1达到同步，由图10和图11的局部放大图可以得出，未加入误差积分反馈律前，电机电压相角不能实现完全跟踪，存在静态误差，加入误差积分反馈律后，系统在积分作用下实现了静态误差的消除，和跟踪信号完全重合；在25 s处加入控制量u2，因控制量u2的跟踪信号为频率信号，和电机电压相角之间存在状态反馈关系，造成了电机电压相角的微小振荡，但其均值仍然服从跟踪信号xd1。从以上分析可以得出，采用考虑静差消除的有限时间命令滤波反步控制方法可以解决传统控制方法存在的稳态误差问题，进一步提高了混沌电力系统控制的精确性。

图10 未加误差积分反馈律δm的控制曲线Fig.10 Control curve of δm without error integral feedback law

图11 加入误差积分反馈律δm的控制曲线Fig.11 Control curve of δm with error integral feedback law

图12和13分别给出了加入误差积分反馈律前后的电机电压相角δm的跟踪误差，未加入误差积分反馈律前，电机电压相角的跟踪误差稳定在0.000 27处，没有实现完全跟踪，并且受到控制信号u2的影响较大，呈正弦波动状态；加误差积分反馈律后，跟踪误差稳定在0处，实现完全跟踪，并且对u2引起的正弦扰动具有一定的抑制效果，未加入误差积分反馈律时，其幅值为0.000 02左右，加入误差积分反馈律后，幅值基本为0，进一步削弱了电力系统控制量u1和u2之间的耦合关系。通过以上两个误差图可以更加直观地得出，加入误差积分反馈律能够有效消除控制过程中产生的静态误差，进一步抑制不同控制变量的耦合对控制效果的影响，可以有效提升混沌电力系统的控制效果。

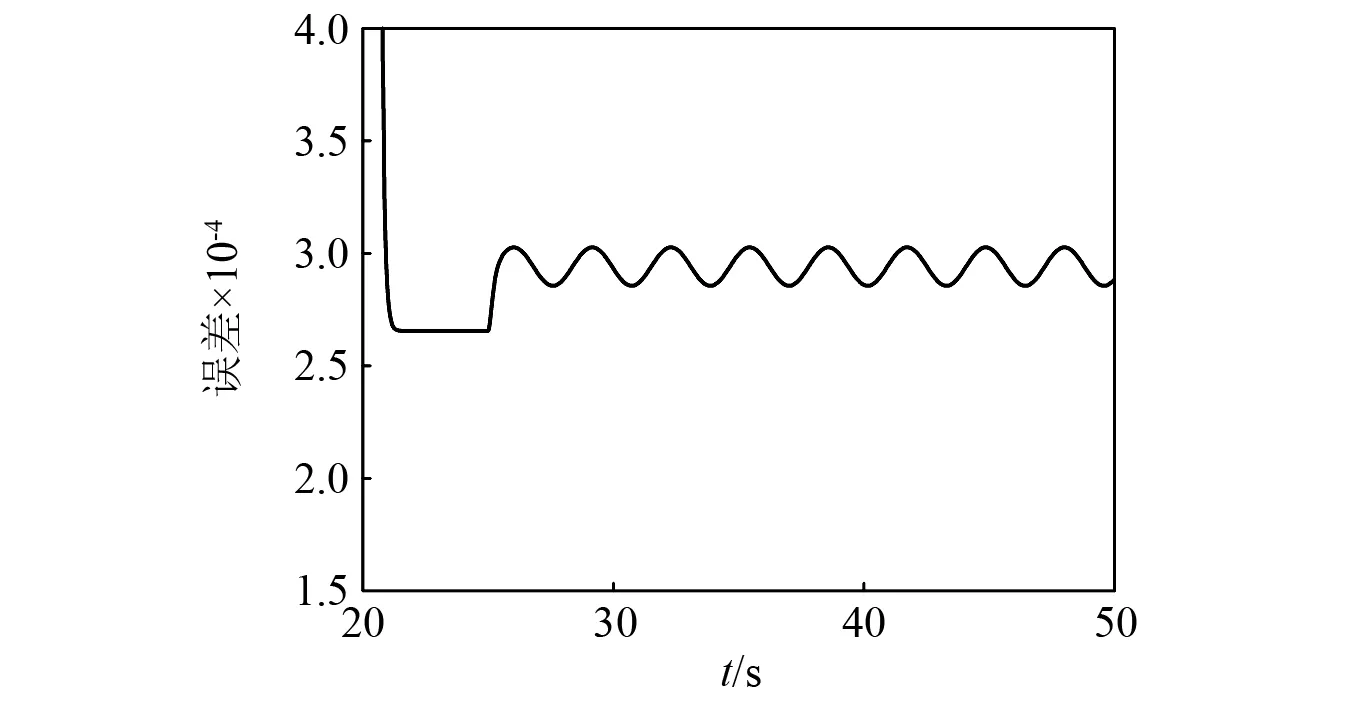
图12 未加误差积分反馈律δm的跟踪误差Fig.12 Tracking error of δm without error integral feedback law

图13 加入误差积分反馈律δm的跟踪误差Fig.13 Tracking error of δm with error integral feedback law

图14和图15给出了加入误差积分反馈律前后负载电压相角δ的跟踪效果。由图14和图15可以得出，在20 s处加入控制量u1，负载电压相角的混沌状态得到了抑制，稳定为常数，在25 s处加入控制量u2，负载电压相角迅速与跟踪信号xd2达到同步。未加误差积分反馈律前，负载电压相角与跟踪信号之间存在直流偏移，具有较为明显的幅值和相位跟踪误差；而加入误差积分反馈律后，跟踪误差随积分的作用逐渐减少，跟踪过程中的幅值和相位偏移得到有效消除，达到了更好的控制效果。从以上分析可以得出，采用考虑静差消除的有限时间命令滤波反步控制方法可以解决传统控制方法在跟踪频率信号幅值和相位上的不足，达到更好的混沌电力系统控制效果。

图14 未加误差积分反馈律δ的控制曲线Fig.14 Control curve of δ without error integral feedback law

图15 加入误差积分反馈律δ的控制曲线Fig.15 Control curve of δ with error integral feedback law

图16和图17给出了加入误差积分反馈律前后负载电压相角δ的跟踪误差曲线，在25 s处加入控制量u2，两者的跟踪误差都向零快速收敛。加入误差积分反馈律前，负载电压相角的跟踪误差最终保持-0.005左右，并存在明显的正弦扰动，不能很好的跟踪频率信号；加入误差积分反馈律后，因积分作用，跟踪误差快速收敛到零，并且正弦扰动也得到了有效抑制，具有更好的频率跟踪控制效果。从以上两个误差图可以清晰得出，加入误差积分反馈律能有效消除频率信号跟踪时存在的直流偏移，抑制了跟踪误差的波动性，进一步提高混沌电力系统控制的可靠性。

图16 未加误差积分反馈律δ的跟踪误差Fig.16 Tracking error of δ without error integral feedback law

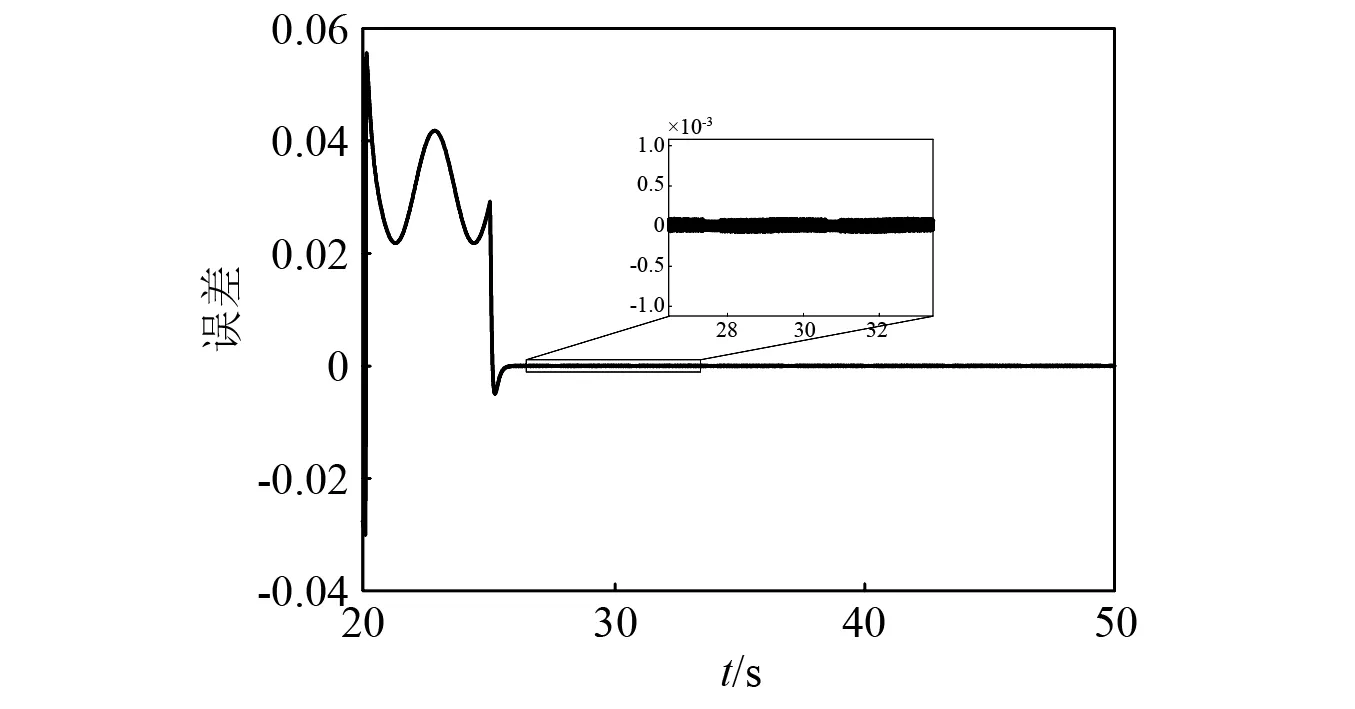
图17 加入误差积分反馈律δ的跟踪误差Fig.17 Tracking error of δ with error integral feedback law

5 结 论

本文以三节点四阶电力系统作为研究对象，揭示了电力系统的混沌振荡现象。为抑制该现象的发生并消除控制过程中存在的跟踪误差，提出一种静差消除的混沌电力系统有限时间命令滤波反步控制方法，给出了详细的公式推导和设计步骤，并证明其能在有限时间内跟踪期望轨道，使系统脱离混沌，间接实现了电力系统的混沌控制。仿真试验表明，采用有限时间命令滤波反步控制，电力系统的电机电压相角δm和负载电压相角δ能够快速地跟踪给定信号，让电力系统脱离混沌状态；加入误差积分反馈律进一步削弱了不同控制量之间的耦合影响程度，解决了该控制方法无法消除静态误差的问题，使电力系统电机电压相角和负载电压相角的跟踪误差分别由0.000 27和0.005收敛至0左右；将控制量u2引起的正弦扰动从幅值为0.000 02收敛至0左右。该控制方法能够有效抑制电力系统的混沌振荡现象，保证了电力系统的安全稳定运行。