高柔塔风电机组塔筒振源特性分析
魏煜锋, 何维令, 蒋祥增, 何宇翔
(明阳智慧能源集团股份公司 风能研究院,广东 中山 528437)
风力发电机组工作环境极为复杂,运行状态下会同时受到风、大地脉动、地震等外部环境载荷以及风轮旋转、偏航、电磁激励等内部运行载荷的联合激励作用,从而导致机组的振动特性变得复杂。塔筒结构作为机组主要的支撑部件,具有轻质、高耸、低阻尼等特点,使得其对各种激励的动力响应更为激烈,过大的振动不仅会对自身产生破坏作用,还会对机组的安全稳定性造成影响。因此,为保证机组能够正常运行,开展塔筒在各种载荷激励下的动力学研究具有重要意义。
目前,国内外对风电机组动力学的研究主要通过数值模拟[1-2]和模态参数识别[3-5]来实现,而对引起结构振动的诱因以及能量分布特性的研究较少。因此,为探究诱发风机结构振动的振源特性和各振源能量分布的变化规律,本文以某140 m级高柔塔风电机组塔筒为研究对象,测量其不同高度处的振动响应信号,利用谱峭度法识别诱发塔筒振动的主要振源类型及其特性,采用小波包分解和小波包能量计算原理对实测信号进行分解得到表征各振源特性的频域分量和能量占比,最后通过对不同工况和不同测点位置的振源特性及其能量占比进行统计,得到了机组在不同工况下各测点的振源及其能量分布规律,该研究成果对机组的健康监测、安全评估以及塔架设计具有较高的实际运用和参考价值。
1 理论基础
1.1 谱峭度
设x(n)是一组实测离散时域随机序列,X(m)是其离散傅里叶变换。一般的,X(m)为复数序列,其二阶累积量和四阶累积量以共轭对形式可以定义为
k2(m)=cum[X(m),X*(m)]
(1)
k4(m)=cum[X(m),X*(m),X(m),X*(m)]
(2)
如果信号属于稳定信号,运用复随机变量的简单变换得到
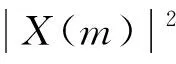
(3)
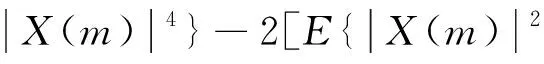
(4)
因此,频谱的峭度值可以定义为[6]
(5)
将时间序列分为M段,并对每段分别做傅里叶变换得Xi(m),(i=1,2,…,M),得到谱峭度的无偏估计式
(6)
线性系统的响应不会改变输入信号的属性。设混合信号x(n)由高斯信号和周期信号组成,即:
x(n)=b(n)+s(n)
(7)
式中:n=1,2,…,N;b(n)为高斯信号序列;s(n)为周期信号序列。b(n)经离散傅里叶变换后为B(n),由式(6)计算出谱峭度值为
(8)
设频率为m0的周期信号为
(9)
经离散傅里叶变换后为S(m)=Aδ(m0)ejφ,其中,δ(m0)为狄拉克函数。由式(6)可计算在m0频率处的谱峭度值为
(10)
根据傅里叶变换的线性性质,混合信号的傅里叶变换结果为X(m)=B(m)+S(m),得到混合信号的谱峭度值为
(11)
谱峭度法最重要的用途之一是检验信号中不同频分振动的属性,即判断信号是具有周期属性或随机属性[7],如果信号中主要成分频率对应的谱峭度值在-1附近波动,那么该信号整体具有周期性质,如果信号中主要成分频率对应的谱峭度值在0附近波动,那么该信号具有随机性质。因此,本文采用谱峭度法来检验塔筒振动响应信号中主要成分频率对应的峭度值来判断引起结构振动的主要振源类型及其频域特性。
1.2 小波包分解和小波包能量计算
小波包分解是基于小波变换的一种信号分解精细算法,能实现对振动响应频带内的多层次均匀划分,不仅具有小波变换的信号低频部分精确分解的优点,还能同时对高频部分进行精确分解[8]。信号通过小波包分解后,信号的全部特征信息均得以保留,从而能大大提高信号分解的完整性[9]。
假定振动信号x(t)的最高频率为fmax,经过小波包的j层分解,可以得到2j个小波包系数[10],其表达式如下
(12)
与这2j个小波包系数相对应的频带为[11]
(13)
将每个小波包系数进行重构可以得到对应的原始信号的小波包分量
(14)
因此,原始信号可以分解为2j个小波包分量的和
(15)
对于原始响应信号x(t),j层小波包分解下的总能量Ex为[12]
(16)
利用小波包分解的正交性条件可得各个频段总能量为
(17)

(18)

(19)
2 工程背景及实施方案
2.1 试验机组概况
试验机组位于河南省信阳市固始县境内,该地区属于平坦地形,风切变及湍流强度较小,适合高柔塔机组的稳定运行。试验机组为半直驱式风电机组,额定功率为3.0 MW,额定转速为11.1 r/min,切入、切出风速分别为2.5 m/s和20 m/s;机组叶轮直径156 m,轮毂中心高度140 m,塔筒为钢制锥筒结构,分为六节,每相邻两节之间通过高强度螺栓连接,从下到上各节的高度分别为17 m,17.5 m,22.5 m,25 m,27.5 m,27.42 m,塔筒总质量约为450 t,设计使用寿命为20年。
2.2 试验系统
硬件数据采集系统采用北京东方振动和噪声研究所研制的INV3068-S2数据采集仪以及中国地震局工程力学研究所研制的941B低频速度拾振器;试验数据的分析基于某开源平台开发的分析程序。
2.3 试验方案
整机塔筒由六节组成,在每节塔筒顶部法兰处各设置一个测点,同时在各个测点的径向和法向各安装一个941B拾振器,共设置6个测点、安装12个拾振器。将各层的传感器通过屏蔽线缆连接到塔基的采集器上进行数据的收集,其测点布置示意图如图1所示。由于机组属于高柔、低频结构,因此将采样频率设置为12.8 Hz,采样时间设置为10 min/组。

图1 测点布置示意图Fig.1 Schematic diagram of measuring point layout
2.4 试验分析流程
本文根据谱峭度法与小波包分解和小波能量理论进行塔筒结构在运行状态下的振源识别和特性分析,其流程如下:
(1)对可能引起柔塔机组振动的各类振源类型及频率进行分析;
(2)选取三种典型工况下的塔筒振动响应数据,通过频域分析与谱峭度法确定机组结构振动响应的主要频率特性和主振源的属性;
(3)对原始信号进行小波包分解,将分解的各子信号中的主频与机组振源激励频率进行一一对应,确定原始信号中存在的主要振源类型;
(4)运用小波包能量原理对分解的各子信号进行能量计算,确定各类振源在振动信号中所占有的能量比重;
(5)对不同运行工况下各振源能量占比进行统计,归纳总结诱发机组振动的主要振源及其能量随机组运行工况的变化规律。
3 振源类型及频率分析
引起柔塔机组塔筒振动的振源类型主要分为三类,即:环境载荷激励引起的塔筒振动、机组运行时风轮旋转激励引起的塔筒振动以及发电机等电磁激励引起塔筒的振动[13]。其中,在运行状态下对风机塔筒振动影响最为关键的振源是以风载荷、大地脉动为主的环境激励以及机组运行的叶轮转频激励。前者引起结构按照固有模态成分进行自激振动,后者则使风机产生周期性的受迫振动。在采集的塔筒振动响应信号中,前者体现的频分主要为机组自身结构的低阶模态——叶片、塔筒低阶固有频率,后者则体现为机组叶轮的转频及其倍频成分[14-15]。
图2(a)为利用锤击法将叶片固定在试验台上测量其激励和响应的频响函数后通过最小二乘复频域法(PloyLSCF)模态参数识别算法得到的柔塔叶片模态稳定图;图2(b)为利用塔筒振动响应数据通过随机子空间(stochastic subspace identification,SSI)运行模态参数识别方法识别的塔筒模态稳定图。表1给出柔塔机组运行工况下引起塔筒振动的各类振源及其频率。
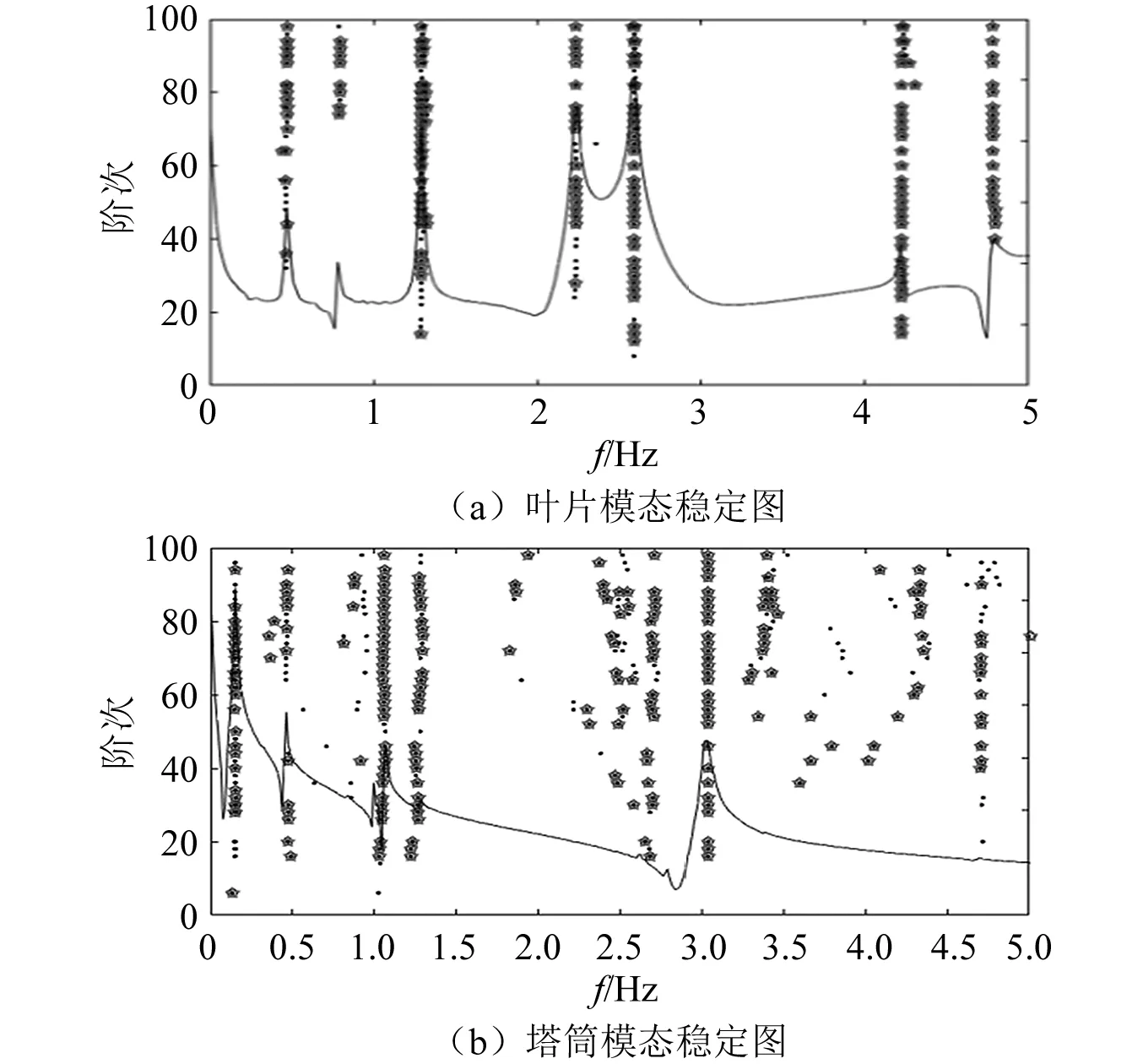
图2 柔塔叶片及塔筒模态稳定图Fig.2 Blade and tower modal stability diagram
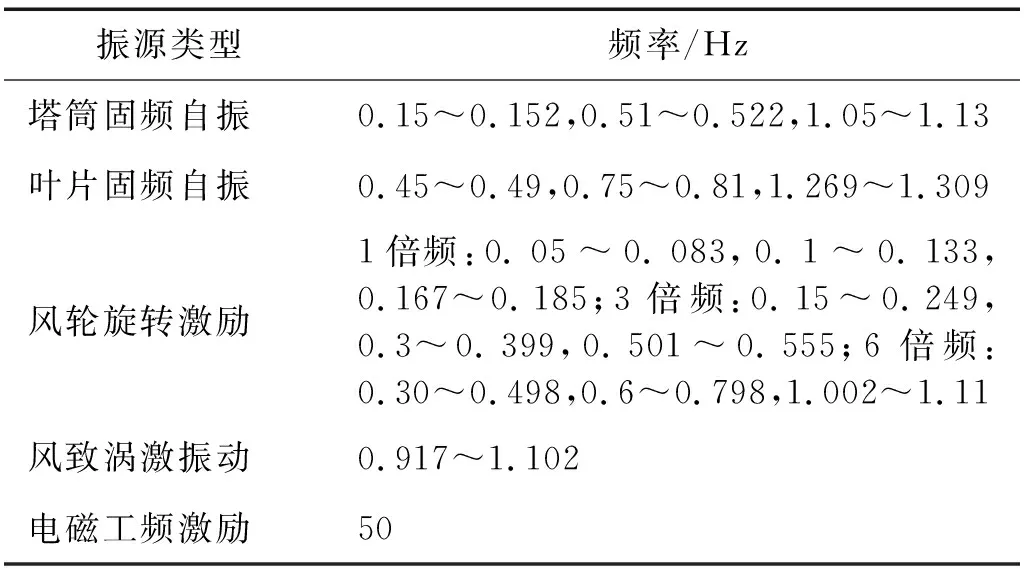
表1 振源类型及频率表Tab.1 Vibration source types and frequencies
4 主振源识别及能量计算
4.1 谱峭度分析
表2和图3分别给出停机、低功率、额定功率三种典型工况下机组运行参数以及对应的塔筒振动响应信号谱峭度图。从图3(a)中可以看出,静止工况下,塔筒振动响应信号中的优势频率为0.15 Hz,体现为塔筒的1阶自振频率,对应的谱峭度值在-1附近,表明在静止工况下,塔筒振动表现为以1阶自振频率的周期性振动;从图3(b)中可以看出,工况2下,塔筒振动响应信号中的优势频率为0.095 Hz,0.15 Hz,分别体现为风轮转频和塔筒1阶自振频率,对应的谱峭度值都在-1附近,表明在该工况下,塔筒振动表现为以风轮转频以及1阶自振频率的多谐波耦合周期性振动;反观图3(c)中,工况3下,塔筒振动响应信号的优势频率为0.185 Hz,对应的谱峭度值在-1附近,表明在该工况下,塔筒振动表现为以风轮转频的周期性振动。
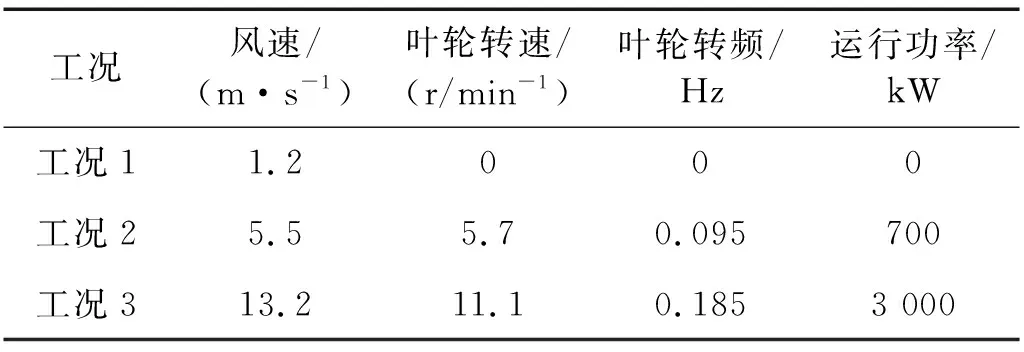
表2 三种工况参数表Tab.2 Parameter table of three working conditions

图3 三种工况下塔筒振动响应信号谱峭度图Fig.3 Kurtosis spectrum of tower vibration response signal under three working conditions
4.2 小波包分解和小波包能量计算
将三种工况数据进行小波包分解,由于塔筒振动响应信号具有周期性,因此小波函数为sym5[16],分解层数为6,共分解成64个子频带,塔筒振动响应信号的采样频率为12.8 Hz,根据采样定理[17],fmax=6.4 Hz,每个子频带的带宽为0.1 Hz。表4给出了三种工况振动响应信号小波分解和小波包能量计算后各频带主频以及能量占比的统计数据,可以发现三种工况的能量主要集中在前面32个子频带中,达到99%以上。其中:工况1时,振动能量主要分布在的第2子频带中,主频为0.15 Hz,体现为塔筒1阶自振频率,能量占比达到93.392%;工况2时,振动能量主要分别分布在第1和第2子频带中,对应主频分别为0.095 Hz,0.150 Hz,体现为风轮转频和塔筒1阶自振频率,能量占比分别达到18.056%,64.912%;工况3时,振动能量主要分布在第2、第6、第10子频带中,对应主频分别为0.185 Hz,0.556 Hz,1.109 Hz,体现为风轮1倍转频、3倍转频以及6倍转频,能量占比分别达到了71.016%,7.838%,18.606%。结合表2给出的风机振源类型及其对应的频率可以看出:在工况1下,塔筒主要受自身1阶自振激励发生周期性的自激振动;工况2下,塔筒主要受自身1阶自振和风轮旋转联合激励发生周期性的自激、强迫耦合振动;工况3下,塔筒主要受风轮旋转激励发生周期性的强迫振动。
由以上分析可以得到,风机塔筒结构在三种工况下的主振源分别为塔筒1阶自振激励、1阶自振和风轮旋转联合激励以及风轮旋转激励,其中1阶自振激励频率体现为塔筒的1阶固频,风轮旋转激励频率体现为风轮的转频及其倍频。
5 振源特性分析
5.1 不同工况主振源变化规律
图4给出峭度值为-1的塔筒响应频率随功率、转速变化的散点图,从图4(a)中可以发现:在功率约300 kW以下时谱峭度值为-1对应的频率为0.15 Hz,体现为塔筒1阶自振频率;300~750 kW谱峭度值为-1的频率体现为塔筒1阶自振频率以及风轮转频;在750 kW以上时,谱峭度值为-1对应的频率为风轮转频,同时可以发现当功率达到2 000 kW以上时,谱峭度值为-1的频率随功率的上升不再增加,由于这时风轮达到额定转速。从图4(b)中可以发现同样的规律:低转速区(<5.5 r/min)塔筒振动响应谱峭度值为-1的频率体现为机组塔筒的1阶自振频率;中转速区(5.5~7.5 r/min)塔筒振动响应谱峭度值为-1的频率体现为塔筒1阶自振频率和风轮转频;高转速区(>7.5 r/min)塔筒振动响应谱峭度值为-1的频率体现为风轮转频,同时可以发现在8.5~10 r/min机组设置了禁止转速区,使风轮转频有效的避开了塔筒1阶自振频率。

图4 谱峭度值为-1的频率随功率、转速变化散点图Fig.4 Scatter plot of frequency with spectral kurtosis value of -1 as a function of power and speed
图5给出了柔塔机组在不同转速工况下各测点主频率的分布图。由图5(a)可知,在低转速工况下,塔筒各个测点的振动主频率分布在0.15~0.152 Hz内,表现为塔筒的1阶自振频率;随着转速的增大,如图5(b)所示,各个测点振动主频率主要分布在0.1~0.133 Hz,0.15~0.152 Hz,0.3~0.4 Hz内,分别表现为风轮1倍转频、塔筒1阶自振频率以及风轮3倍转频,同时在1.0~1.2 Hz内也有少量分布,体现为塔筒的2阶自振频率;在高转速区,如图5(c),各个测点振动响应主频率集中在0.167~0.183 Hz,0.5~0.6 Hz,1.0~1.2 Hz三个频率范围内,分别表现为风轮1倍转频、3倍转频、6倍转频,而在其他频率区分布较少。
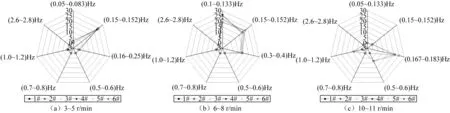
图5 不同转速工况下各测点响应主频分布统计图Fig.5 The main frequency distribution statistics diagram of the response of each measuring point under different speed conditions
根据以上分析,可知引起塔筒结构振动的主要激励源在不同工况下表现不同,其中,在低转速工况下,塔筒1阶自振激励为主振源;中转速工况下,塔筒1阶自振和风轮旋转联合激励为主振源;在高转速工况下,风轮旋转的转频激励为主振源,同时发现在高转速区风轮3倍频和6倍频和塔筒的固有模态频率重合,可能引起机组的共振,从表3工况3的能量分布也可看出,在3倍频和6倍频处对应的能量占比较大。
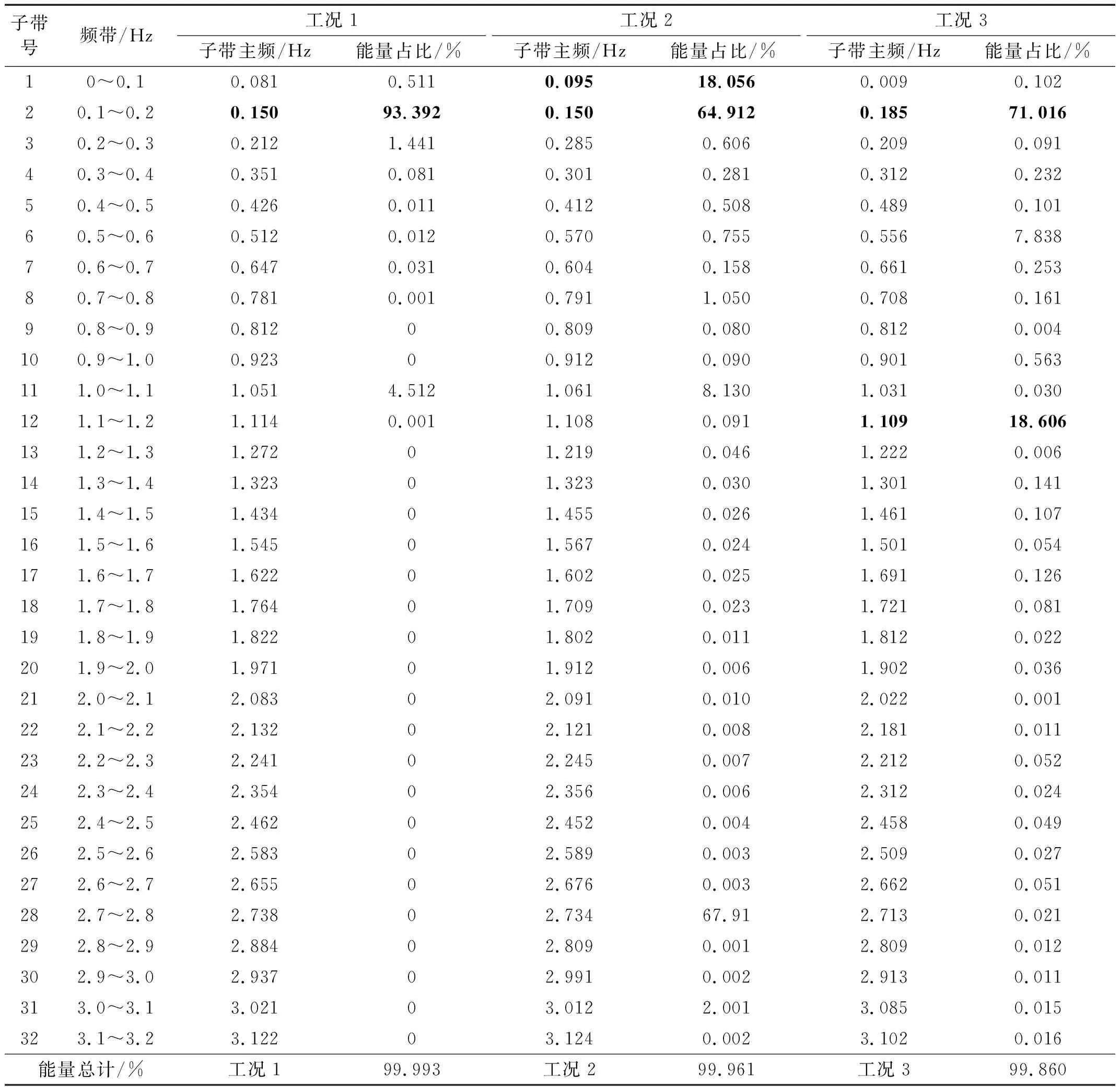
表3 三种工况小波包分解子带主频与能量占比统计表Tab.3 Three working conditions wavelet packet decomposition sub-band dominant frequency and energy ratio statistics table
5.2 不同测点各振源能量变化规律
图6给出转速为8 r/min、功率750 kW工况下1#、3#、5#测点振动响应信号主要振源及能量占比图。该工况下塔筒受机组自振与风轮旋转联合激励作用,图中可以看出,风轮转频及倍频、塔筒固频自振能量占总能量的90%以上,这两种激励源为诱发塔筒振动的强振源。随着塔筒位置的变化两种强振源能量分布有所不同,随着测点位置的降低,风轮转频及倍频激励引起塔筒振动的能量在降低,塔筒自激引起塔筒振动的能量在增加。以上表明,在该工况下,风轮旋转激励对塔筒上部振动影响大,机组自振激励对塔筒下部振动影响大。
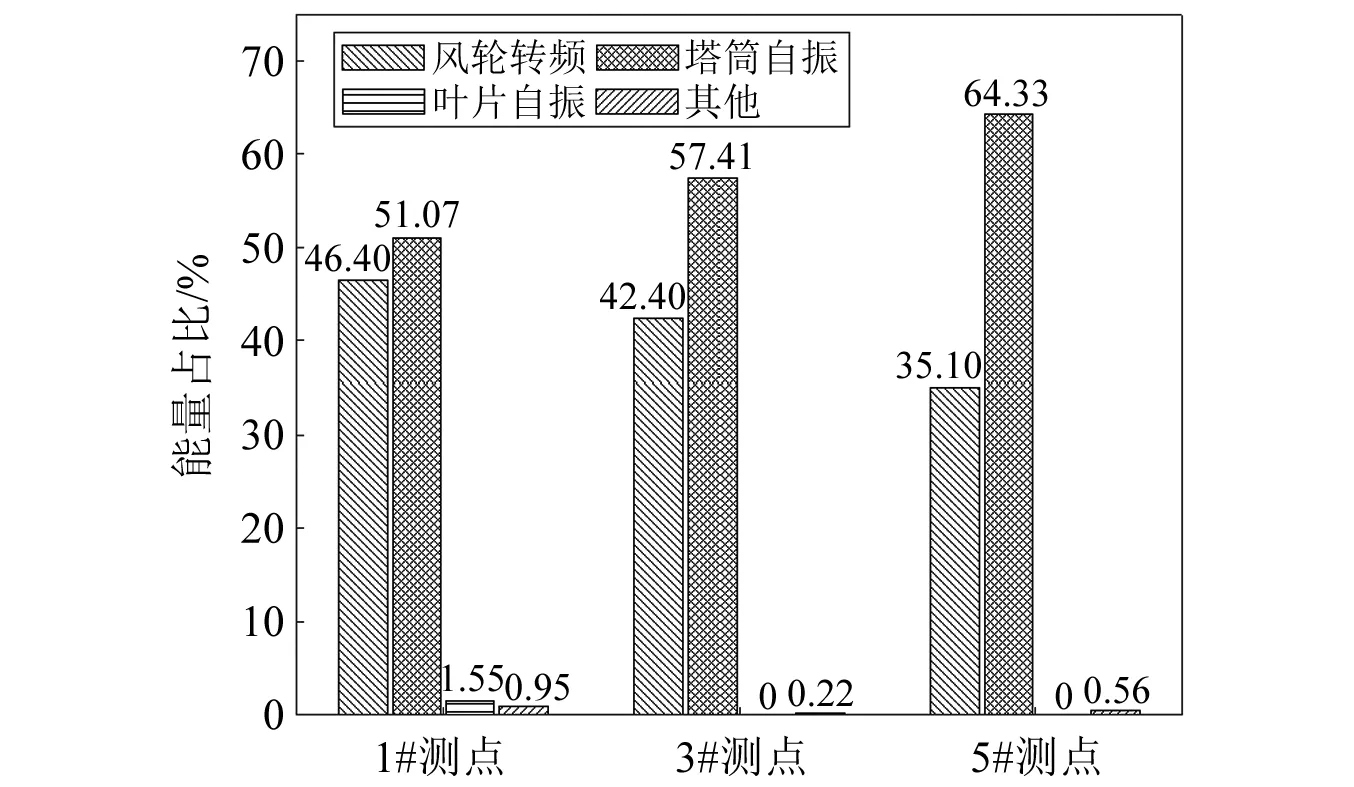
图6 不同测点各振源能量占比图Fig.6 Energy ratio diagram of each vibration source at different measuring points
5.3 不同工况主振源能量变化规律
图7给出机组塔筒1#、3#、5#测点处塔筒1阶自振激励与风轮旋转激励的能量占比随功率变化趋势图。从图中可以看出各测点两种主要振源能量占比随功率变化趋势一致,随着机组功率的增加,塔筒1阶自振激励能量占比逐渐减少,风轮旋转激励能量逐渐增加。在400 kW以下时,各测点塔筒1阶自振激励能量占比高达75%以上,占据主导作用;随着机组功率升高,在600~800 kW时,塔筒振动既受1阶自振激励影响也受风轮旋转激励影响,两者对塔筒振动的贡献相当,能量占比在30%~60%;当机组功率达到1 000 kW以上时,风轮旋转激励能量达到70%以上,占主导作用,并且在机组功率达到1 600 kW以上时,风轮旋转激励能量占比达90%以上,诱发塔筒振动的贡献几乎来自风轮旋转激励,塔筒1阶自振激励影响作用几乎可以忽略不计。
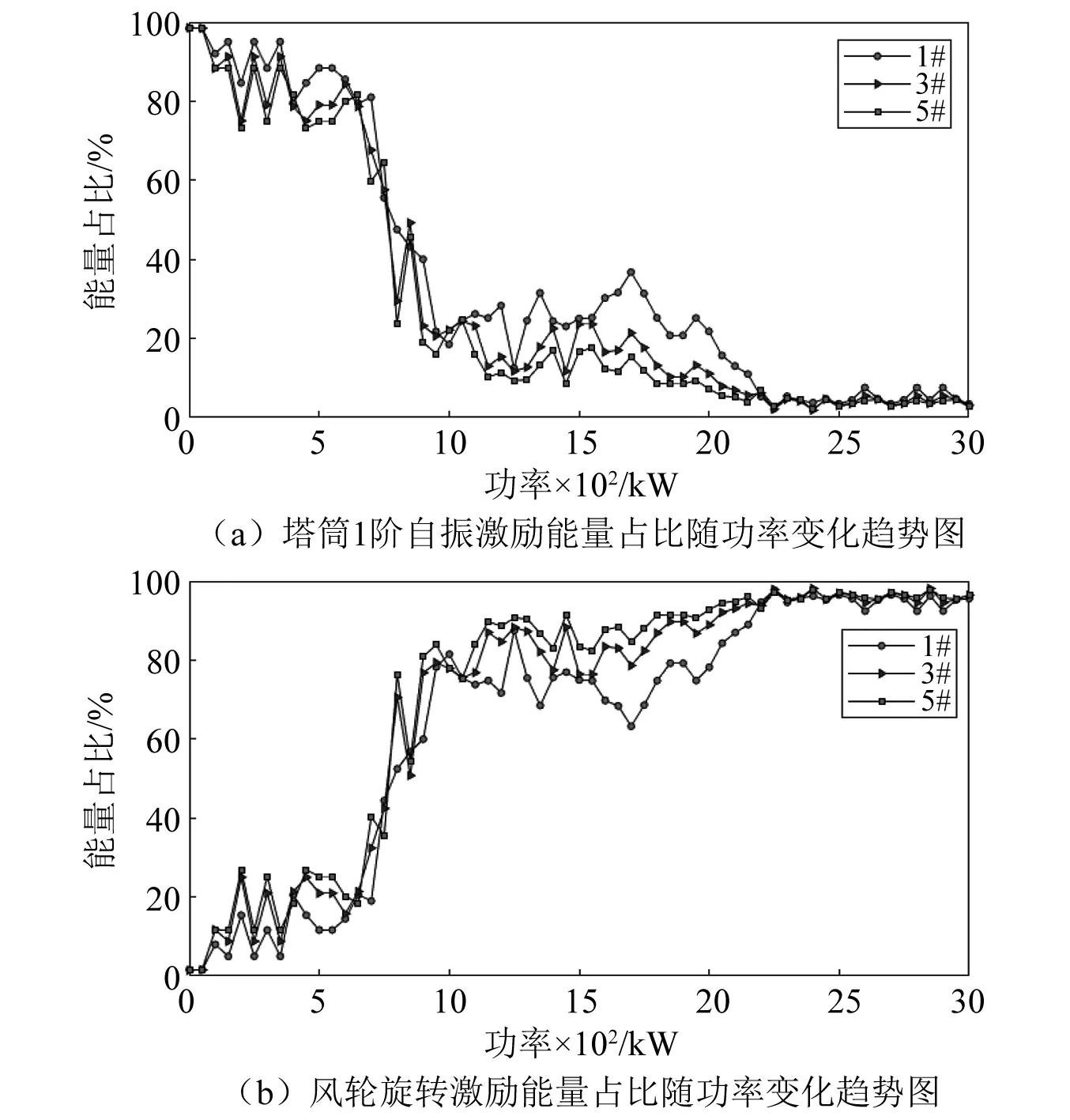
图7 不同测点各主振源能量占比随功率变化趋势图Fig.7 Trend graph of the energy ratio of each main vibration source at different measuring points vs. power
5.4 中高功率区转频与倍频能量对比
图8给出1 000 kW以上功率区各个测点转频激励及倍频激励能量占比图,由图中可以看出,当功率达到1 000 kW以上时,风轮的转频及倍频激励能量占比达70%以上,由此可知中高功率区诱发塔筒振动的主要振源来自风轮旋转激励。其中,塔筒上部测点主要受风轮转频激励作用,1倍频激励能量占比达60%以上,下部测点主要受6倍频激励作用,能量占比基本在40%~70%,远超过1倍频激、3倍频励能量占比,通过分析这一区间风轮转速,在该功率区间,风轮转速维持在10~11 r/min,对应的6倍转频为1~1.1 Hz,刚好和塔筒的2阶弯曲模态频率接近,从而引起塔筒共振,导致下部测点的振动响应在6倍频附近能量占比很大。针对机组的安全评估,机组虽然设置了共振穿越控制程序,但主要考虑的是避免风轮转频(1P)和塔筒1阶自振频率重合,但实际运行中,风轮的谐波激励对机组振动影响也较大,在高转速区,风轮3倍频、6倍频与塔筒的扭转和二阶固有频率接近,容易引发机组的共振。
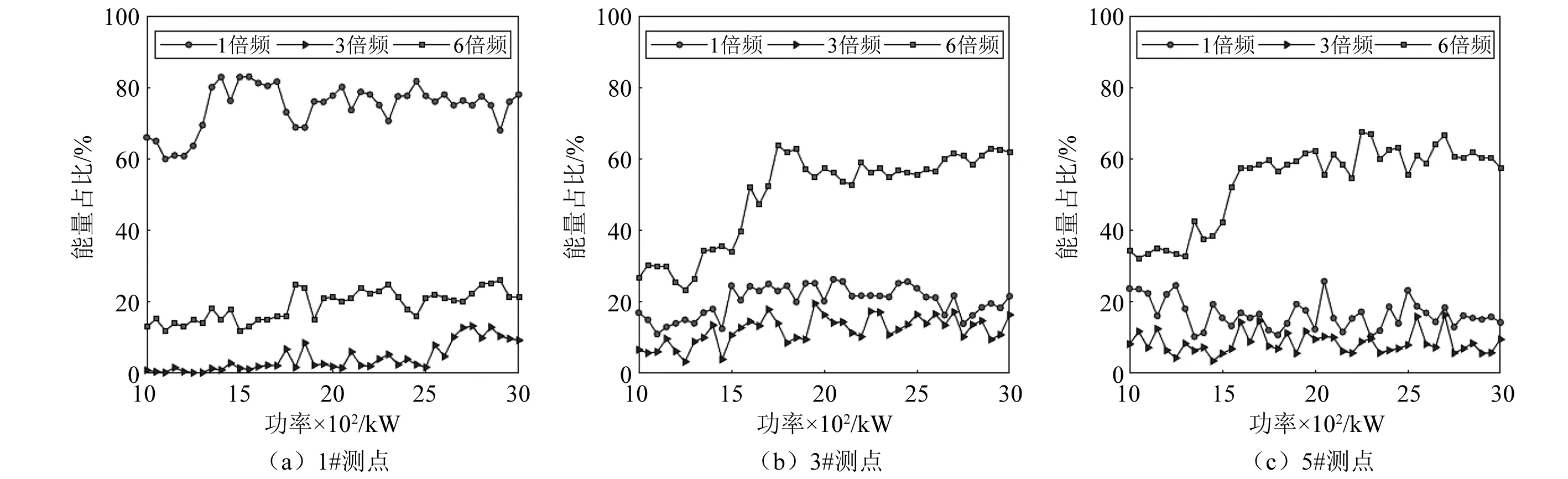
图8 中、高功率区各测点转频与倍频激励能量占比图Fig.8 Frequency conversion and frequency doubling excitation energy proportion diagram of each measuring point in the middle and high power areas
6 结 论
高柔塔机组具有轻质、高耸、低柔等特性,使得塔筒结构对各种激励的动力反应更为敏感。本文通过测量塔筒不同高度处的振动响应信号,基于谱峭度法和小波包分解以及小波包能量理论分析方法,从频域和能量的角度来分析运行状态下引起机组振动的主要振源类型及其能量变化规律,主要得到以下结论:
(1)运行状态下机组结构振动主要受到塔筒低阶自振激励和风轮旋转激励影响,这两种激励是诱发塔筒振动的主要振源,前者频率体现为塔筒的1阶自振频 率,后者频率体现为风轮转频及倍频。通过谱峭度分析,两者频率对应的峭度值都在-1附近,说明高柔塔机组塔筒在整个生命周期内始终都受到周期性的强振源激励作用。
(2)在不同运行工况下,两种主振源贡献不同:在低功率、低转速工况下,塔筒1阶自振激励为主要振源,起主导作用,风轮旋转激励作用影响较小;中功率、中转速工况下,两者贡献相当,机组同时受到塔 筒 自振激励和风轮旋转激励影响;在高功率、高转速工况下,风轮旋转激励为主要振源,起主导作用,塔筒自振激励影响较小。
(3)不同高度位置处两种振源能量占比不同,其中,上部位置风轮旋转激励能量占比较大,下部位置塔筒自振激励能量占比大。
(4)机组虽然设置了共振穿越控制程序,但主要考虑的是避免风轮转频(1P)和塔筒1阶自振频率重合,但实际运行中,风轮的谐波激励对机组振动影响也较大,在高转速区,风轮3倍频、6倍频与塔筒的固有频率接近,容易引起机组的共振,影响机组的安全稳定性,因此在机组的塔筒设计时还应考虑风轮转动倍频与其固有频率间的关系,适当加大塔筒结构固有频率与风轮3倍频和6倍频之间的安全裕量以保障机组运行时的安全稳定性。

