超音速流-热载作用下梯度多孔壁板的非线性振动特性分析

韩明君， 李金佩， 王 鹏

(兰州理工大学 理学院, 兰州 730050)

高超音速飞行器由于其具备高速度、高机动、突防能力强、被探测到概率低、作战半径和效能高等诸多优点，已经成为各大国下一代航天器、飞机、导弹等不可或缺的条件和主要的发展方向。凭借速度和高度的绝对优势，高超音速飞行器可以在短时间内完成高难度的情报、监视、侦察和打击任务，已经引起了国际社会对其广泛的关注和讨论。尤其是对于飞行器中的壁板结构，由于其自身的弹性变形会受到温度荷载、气动力、以及材料自身属性的影响，在这些作用的影响下，壁板会产生复杂的非线性动力学响应，从而容易使壁板结构产生疲劳损伤，进而影响飞行器结构的疲劳寿命[1-2]。多孔金属材料与传统质密金属材料相比，具有超轻、高比强、高比刚度、高强韧、高能量吸收等优良机械性能, 以及减震、散热、吸声、电磁屏蔽等特殊性质, 它兼具功能和结构双重作用,是一种性能优异的多功能材料[3]。综合来看，金属多孔材料能大幅度提升高超音速飞行器的各项参数及性能，是一项值得关注的研究方向。

近年来，国内外许多学者对超声速气流中壁板非线性气动弹性响应行为开展了许多研究。Cheng等[4]运用超高速气流作用下壁板非线性颤振的有限元时域模态， 分析了混沌状态下壁板的屈曲、极限环振荡、周期以及时域图和相位图等。Ghoman等[5-6]基于有限元方法对壁板颤振问题进行了研究。Koo等[7]用有限元方法讨论了阻尼对复合材料板颤振性能的影响。Ibrahim等[8-11]在超音速气流中考虑了二维壁板的剪切变形，分析了壁板的气动弹性模态。他们也考虑了平面内热载荷对板壳结构横向弯曲挠度的影响，研究了均匀温度场中复合材料板壳的颤振和热屈曲问题。李丽丽等[12]在非定常气动力壁板模型中引进了热荷载的影响，得到了热壁板的颤振方程。杨智春等[13]基于Von Kármán非线性板理论和Galerkin方法建立超音速气流中二维受热壁板的气动弹性模型。王广胜等[14-15]对超音速流中飞行器的受热平壁板和曲壁板非线性气动弹性稳定性进行了深入研究，分析热气动弹性系统的颤振边界特性以及不同的参数组合对系统颤振临界动压与稳定性的影响。周建等[16]用POD方法构造三维复合材料曲壁板颤振响应模态，通过数值积分方法计算三维复合材料曲壁板的颤振响应，计算结果与传统的模态缩减法取得一致。梅冠华等[17]采用流-固耦合算法研究了曲壁板在跨/超声速气流下的气动弹性特征，为高速飞行器的壁板设计和颤振抑制提供了依据。

综上所述，近年来主要集中研究传统质密金属材料的气动稳定性，对多孔金属材料的气动弹性鲜有研究。本文基于Von Kármán薄板大挠度理论和Kirchhoff假设，考虑孔隙沿矩形板厚度方向呈三种不同的分布方式，利用Galerkin法研究了温差、孔隙率、气动刚度系数对梯度多孔薄壁板气动弹性的影响，并用Runge-Kutta法给出了系统的时间历程图、相位图和庞加莱截面映射图。

1 模型建立与方程处理

建立梯度多孔二维壁板在超音速气流中的力学模型，如图1所示。假设温度在厚度方向均匀分布，温度变化为ΔT的简支无限展长的壁板模型，其长度为L,厚度为h，密度为ρ(z)，弹性模量为E(z)，α(z)为材料的热膨胀系数，μ为沿矩形板厚度方向恒定的泊松比[18]。在其上表面有沿x方向的超音速气流,流速为U∞，马赫数为M∞，空气密度为ρ∞。

图1 运动模型图Fig.1 Motion model

本文考虑了孔隙沿厚度方向呈均匀分布和两种非均匀分布[19-21]

孔隙均匀分布

E(z)=E1(1-θγ)

(1)

(2)

α(z)=α1(1-amγ)

(3)

孔隙关于几何中面均匀分布

(4)

(5)

(6)

孔隙关于几何中面非均匀分布

(7)

(8)

(9)

2 基本方程的建立及处理

2.1 建立控制方程

基于Von Kármán薄板大挠度理论，假定温度场是准定常的，并且只考虑板的横向振动，应变位移关系为

(10)

(11)

式中，u,v和w分别为x,y和z轴的位移。根据Hooke定律，应变表示为

(12)

(13)

对于无限展长的二维壁板，可以忽略εy，由式(10)～式(13)可得

(14)

式中，NT为ΔT引起的温度应力。考虑Kirchhoff假设，壁板的振动微分方程为

(15)

式中：Mx为弯矩；Nx为面内力；mx为板的单位长度的质量；qa为气动力。其中

(16)

(17)

(18)

将E(z),ρ(z)和α(z)的表达式和式(10)、式(14)和式(16)～ 式(18)代入振动微分方程式(15)中得到

(19)

式中：D0为矩形板的最大抗弯刚度；ek1为对参变量的影响，k=1,2,3为不同孔隙分布，由于多孔壁板的边界为二端简支，则u|x=0.L=0,边界处的弯矩为零

(20)

(21)

又由于面内力为常数，对其取x方向的平均值，由式(14)和式(21)，振动微分方程式(19)中的面内力可以表示为

(22)

将式(22)代入振动微分方程式(19)中，可以得到多孔壁板的振动微分方程

(23)

(24)

(25)

对于孔隙均匀分布

e11=1-θγ,e12=1-θγ,

(26)

对于孔隙几何中面均匀分布

(27)

对于孔隙几何中面非均匀分布

(28)

2.2 微分方程的无量纲化

引入如下无量纲参数

将无量纲参数代入多孔壁板的振动微分方程式(22)中，得到无量纲微分方程

(29)

(30)

(31)

考虑对边简支壁板在x=0和x=1处的无量纲边界条件，其形式如下

(32)

3 Galerkin法求解屈曲和静态分岔问题

(33)

两端简支的二维壁板的边界条件为

ψ|x=0,1=0，ψ″|x=0,1=0

(34)

ψ(4)+λ2ψ″=0

(35)

无量纲微分方程式(35)的通解为

(36)

将式(36)代入二维壁板的边界条件式(34)中可得

(37)

式(36)中ψ(x)应具有非零解，因此线性齐次方程的系数行列式为零化简可得特征方程，由式(37)的行列式可得特征方程的解为

csinλ=0或λ=mπ

(38)

λ2=Q-Γ=Q-3(ek2/ek1)c2λ2

(39)

由式(39)可以得到

(40)

从而得到

(41)

为了研究热应力对二维壁板的影响，本文通过算例展开讨论。取壁板的材料特性参数E1=78.55 GPa，μ=0.3，L=0.5 m，h=0.002 m。选取壁板1/4长度处进行计算，得到其前三阶弯曲构型的静态分岔图如图2所示。

在第一阶临界屈曲载荷Q1之前壁板都是稳定的；随着轴向力Q的增加，当Q=Q1时，壁板开始出现分岔，发生屈曲,当Q>Q1时，原先在x=0处的平衡点变为不平衡点; 随着轴向力Q的继续增加，当Q大于第二阶临界屈曲载荷Q2时,壁板存在三种平衡：静平衡构型、屈曲构型和新的屈曲构型；当轴向载荷Q继续增加，大于第三阶临界屈曲载荷Q3时，壁板就会存在三个屈曲构型。

由图2和表1计算可知：当孔隙率θ=0时，三种不同孔隙分布壁板的临界屈曲载荷数值相同的，并且与王广胜的研究结果一致；随着孔隙率的增大，三种不同孔隙分布壁板的前三阶弯曲构型的临界屈曲载荷也随之增加，这是壁板中的孔隙削弱了壁板的整体刚度，同时也减小了壁板中的温度应力和面内力，所以前三阶弯曲构型的临界屈曲载荷随着孔隙率θ的增大而增加。

图2 不同孔隙分布的前三阶弯曲构型的静态分岔图Fig.2 Static bifurcation diagrams of the first three order bending configurations with different pore distributions

表1 不同孔隙率前三阶弯曲构型的静态分岔临界屈曲载荷Tab.1 The static bifurcation critical buckling load of the first three order bending configuration with different porosity

当0<θ<0.3时，均匀分布比几何中面非均匀分布先到达临界点，出现分岔；当0.3≤θ≤0.5时，几何中面非均匀分布比均匀分布先到达临界点，出现分岔；当0<θ≤0.5，几何中面均匀分布比其他二种分布都先到达临点，出现分岔，这是因为三种不同的孔隙分布对壁板的整体刚度、温度应力和面内力的影响不同而出现的情况。

4 Galerkin法求解振动问题

4.1 非线性常微分方程组的处理

利用Galerkin法，将简支边界的位移函数表示为正弦函数的线性组合

(42)

(43)

(44)

其中，

(45)

(46)

非线性常微分方程式(46)写成矩阵形式

(47)

4.2 系统发生Hopf分岔的边界曲线

参考文献[22-24]利用Hurwitz行列式，将Hopf分岔的判定转化为非线性方程求根的问题，解决Hopf分岔的代数判据和计算。假设系统的一个平衡点为X0(0,0,0,0)，则该平衡点处的Jacobi矩阵为

(48)

对应的特征方程为det(JA-λI)=0，即

(49)

得到一个关于λ的四次方程

a0λ4+a1λ3+a2λ2+a3λ+a4=0

(50)

其中，

a0=1，

(51)

计算相应的各阶Hurwitz行列式

Δ1=a1

(52)

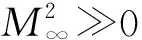
(53)

(54)

由Δ3=0可得无量纲临界流速Ucr为

(55)

(56)

(57)

设向量X=(x1,x2,x3,x4和Y=(y1,y2,y3,y4)T分别是矩阵A的属于特征值iω的归一化的左、右特征向量。根据XA=iωA,YA=iωA,XA=1，可得

(58)

(59)

A2=33π4ek1ek4+π4ek1-9π2ek3ek4RT0,

(60)

(61)

ζ1,2(P1)=α1(P1)±iω(P1)

(62)

式中，α1(P1)=0,ω(P1)>0。于是X(P1)A(P1)·Y(P1)=α1(P1)±iω(P1)，得到

(63)

a1>0,a2>0,…,an>0
Δn-1=0,Δi>0(i=n-3,n-5,…)

(64)

此时系统发生Hopf分岔，即在U=Ucr时超音速流中的壁板发生颤振。

4.3 数值算例

选取杨智春教授等研究的某铝合金壁板材料模型的计算参数，其机械性能参数如表2所示。

表2 某铝合金机械性能参数Tab.2 Mechanical property parameters of an aluminum alloy

假设飞行器的飞行高度为1.1 km，此时空气密度0.364 kg/m3，音速295.065 m/s，马赫数为5。当孔隙率为0时，代入数据可以得到各参数的数值，表3中本文退化数据与曹丽娜研究中的数据基本一致。

表3 RT0=3π2/4时无量纲临界流速和无量纲临界频率等数据Tab.3 Critical velocity and critical frequency data at RT0=3π2/4

取相同材料特性参数,得到随着孔隙率增长不同分布和不同温度应力的壁板的无量纲临界流速和无量纲临界频率。

由图3、图4、图5可知，当孔隙率一定时，随着温度应力的减小，三种不同分布的壁板发生颤振的无量纲临界流速在不断的增大；当温度应力一定时，随着孔隙率的增长三种不同分布壁板的无量纲临界流速都在下降，其中均匀分布中壁板无量纲临界流速随着孔隙率的增加而下降的程度最大，几何中面非均匀分布壁板无量纲临界流速随着孔隙率的增加而下降的程度次之，几何中面均匀分布壁板无量纲临界流速随着孔隙率的增加而的程度最小。壁板无量纲临界频率随着不同孔隙率和温度应力的变化比较复杂。当孔隙率一定时，随着温度应力的减小，三种不同分布的壁板无量纲临界频率都在在不断增大；随着孔隙率的增长三种不同分布壁板的无量纲临界频率也与它初始温度应力有关系，当温度应力小于3π2/4时，几何中面均匀分布壁板无量纲临界频率随着孔隙率的增加而增大，均匀分布壁板和几何中面非均匀分布壁板的无量纲临界频率随着孔隙率的增加而减小；当温度应力大于5π2/4时，几何中面均匀分布壁板和几何中面非均匀分布壁板的无量纲临界频率随着孔隙率的增加而增大，均匀分布壁板的无量纲临界频率随着孔隙率的增加先增加后减小，这是由于对三种不同孔隙分布壁板的整体刚度、温度应力、等效质量和面内力减弱程度不同，三种不同孔隙分布壁板的无量纲临界流速和无量纲临界频率变化趋势也不一样。

图3 RT0=5π2/4时的无量纲临界流速和无量纲临界频率Fig.3 Dimensionless critical velocity and dimensionless critical frequency at RT0=5π2/4

图4 RT0=3π2/4时的无量纲临界流速和无量纲临界频率Fig.4 Dimensionless critical velocity and dimensionless critical frequency at RT0=3π2/4

图5 RT0=π2/4时的无量纲临界流速和无量纲临界频率Fig.5 Dimensionless critical velocity and dimensionless critical frequency at RT0=π2/4

4.4 稳定性验证及分析

超音速流中受热壁板系统在平衡点X0(0,0,0,0)处发生Hopf分岔。即超音速流中受热壁板系统在无量纲动压到达P1时将发生颤振。当无量纲动压小于P1，超音速流中受热平壁板在平衡点是稳定的，而当无量纲动压大于P1时，超音速流中受热平壁板在平衡点是不稳定的。为了验证以上结论，计算了不同参数时对应的平衡点处Jacobi矩阵的特征值。

当θ=0.05,P1=190,RT0=3π2/4时，初值取(0.005, 0.005,0.01,0.01)，给出了系统的时间历程图、相位图和庞加莱截面映射图。

由表4、表5、表6和图6可以得出并验证：超音速流中受热壁板系统在无量纲动压到达P1时将发生颤振，当无量纲动压小于P1时，平衡点的四个特征值全部具有负实部，超音速流中受热平壁板在平衡点是稳定的；而当无量纲动压大于P1时，平衡点的四个特征值中，一对复特征值具有负实部；另一对复特征值具有正实部,超音速流中受热平壁板在平衡点是不稳定的，在其附近产生稳定的极限环。随着孔隙率和温度应力的增大都会让无量纲动压P1减小，从而使壁板有稳定变为不稳定的趋势。

表4 θ=0.5, RT0=π2/4的Jacobi矩阵的特征值Tab.4 Eigenvalues of Jacobi matrices of θ=0.5, RT0=π2/4

表5 θ=0.5, RT0=3π2/4的Jacobi矩阵的特征值Tab.5 Eigenvalues of Jacobi matrices of θ=0.5, RT0=3π2/4

表6 θ=0.3,RT0=3π2/4的Jacobi矩阵的特征值Tab.6 Eigenvalues of Jacobi matrices of θ=0.3,RT0=3π2/4

图6 三种分布的时间历程图、相位图和庞加莱映射图Fig.6 Time history diagram, phase diagram and Poincare map of three distributions

5 结 论

本文基于von Kármán薄板大挠度理论和Kirchhoff假设建立了多孔壁板在超音速流中振动的控制微分方程并无量纲化，然后运用Galerkin法对梯度多孔壁板进行变换并对气动弦长进行积分得到非线性方程，再利用Hurwitz行列式将Hopf分岔的判定转化为非线性方程的求根。最后分别分析了各参数值的变化对无量纲临界频率和无量纲临界流速的影响，并验证了梯度多孔薄壁板气动弹性的稳定性，得到主要结论如下：

(1) 随着孔隙率的增大，三种不同孔隙分布壁板的前三阶弯曲构型的临界屈曲载荷也随之增加，这是由于壁板中的孔隙削弱了壁板的整体刚度，同时也减小了壁板中的温度应力和面内力，前三阶弯曲构型的临界屈曲载荷随着孔隙率的增大而增加。

(2) 当孔隙率一定时，随着温度应力的减小，三种不同分布的壁板发生颤振的无量纲临界流速在不断的增大；当温度应力一定时，随着孔隙率的增长三种不同分布壁板的无量纲临界流速都在下降；当孔隙率一定时，随着温度应力的减小，三种不同分布的壁板无量纲临界频率都在在不断增大。

(3) 超音速流中受热壁板系统在无量纲动压到达P1时将发生颤振；当无量纲动压小于P1时，超音速流中受热平壁板在平衡点是稳定的；而当无量纲动压大于P1时，超音速流中受热平壁板在平衡点是不稳定的，在其附近产生稳定的极限环。随着孔隙率和温度应力的增大都会让无量纲动压P1减小，从而使壁板有稳定变为不稳定的趋势。