一种非完全覆盖多镀层微圆板谐振器热弹性阻尼通用计算框架
杨龙飞, 李 普, 叶一舟, 方昱斌
(1.南京理工大学 智能制造学院, 南京 210094; 2. 东南大学 机械工程学院, 南京 211189; 3. 重庆大学 光电工程学院, 重庆 400094)
随着5 G物联网时代飞速发展,体积小、精度高、耗能小的微机电系统(micro-electro-mechanical system, MEMS)呈现爆炸式增长[1],微机械谐振器是MEMS传感器和执行器的核心器件[2]。品质因子(quality-factor, Q-factor)是衡量微谐振器精度和分辨率的关键参数之一,其倒数可理解为系统阻尼[3]。微机械谐振器运行时主要存在内部阻尼和外部阻尼两种[4]。外部阻尼主要包括空气阻尼和支撑阻尼,空气阻尼可通过超低真空封装消除;支撑阻尼可通过优化锚区的结构阻断应力波。但内部阻尼只能降低,不能被完全消除,主要表现为热弹性阻尼,并已被试验证实[5]。TED本质是振动过程中不均匀应力场产生的温度梯度,在弛豫过程中熵增造成的能量损失。通过研究微谐振器中TED的机理研究可为结构优化设计提供理论支撑,有助于提高其Q-factor值。因此,近几年来研究人员和工程技术人员对TED的关注度一直很高。
Zener[6]于1937年首次提出了薄梁的TED解析模型,并给出了简单模型形式,被科研和工程设计领域广为使用。2000年,Lifshitz等[7]采用新思路推导出基于复频率法的热弹性阻尼解析模型(以下简称L-R模型)。Zener模型和L-R模型为后续研究各种微谐振器件TED奠定了基础。2009年,Sun等[8]提出了轴对称单层微圆板谐振器TED解析模型。2012年,Li等[9]提出了考虑z向应变的微矩形板和圆板的TED模型,研究发现矩形板和圆板的TED表达式完全相同。2021年,Zhou等[10]提出了考虑非局部效应和双迟滞效应微圆板TED模型。
随着镀膜工艺日趋完善,MEMS采用多层结构满足更多的功能性和多样性需求,极大扩展了其应用场景。比如金属膜经常用于电极、质量检测器、光学反射、磁性单元和热导体等。2018年,Liu等[11]提出了考虑双层微圆板谐振器轴向和厚度方向热传导的TED借些模型。2020年,Li等[12]推导出功能梯度微圆板谐振器TED理论模型。
以上双层微圆板TED模型均以镀层与基底完全覆盖为出发点进行研究。实际应用中,机械夹紧和电绝缘导致镀层几乎不可能完全与基底重合。Sandberg等[13]通过试验证实,即使很薄的金属镀层也会导致Q-factor大幅度下降,并建议在基底进行部分区域镀膜,以提高Q-factor。本文提出了一种通用理论框架,可计算具有多个非完全覆盖镀层微圆板谐振器TED。该模型可退化为完全覆盖双层微圆板TED模型[14],并利用ANSYS验证了当前模型的有效性。此外,本文提出了可用工程领域快速计算的简单模型,并分析简单模型的适用范围。最后研究了具有2个非完全镀层微圆板TED频率谱特性。
1 理论框架
1.1 动力学方程求解
以轴对称周边固支微圆板谐振器为研究对象,在圆板径向布置有m(m≥1)个同心镀层,几何模型如图1所示。假设基底层和镀层是均质、各向同性和线性热弹性体。

图1 多镀层微圆板谐振器结构示意图Fig.1 Schematic diagram of a circular microplate resonator partially covered by n coatings
镀层改变了基底抗弯刚度,覆盖区域变为双层结构,未覆盖区域仍为单层结构。将结构整体划分为2m+1个子区域R{p},上标{p}为各子区域索引,p=1,3,5,…,2m+1代表未覆盖区,p= 2,4,6,…,2m表示覆盖区。覆盖区中基底层厚度为hs,半径为rs。圆柱坐标系(r,φ,z)固定在圆板圆心O处。下标k表示第k个镀层,k=1,2,3,…,m。第k个镀层内、外半径分别为r{p=2k-1}和r{p=2k},厚度为hk。子区域r{2k-2}≤r 子区域R{p}简谐线性轴对称振动的振型函数设为 (1) Kirchhoff-Love板的转动惯量和剪切力对控制方程的影响可忽略,自由振动控制方程可设为[15] (2) 式中:ω=2πf为角频率;D{p}为子区域等效抗弯刚度。 (3) (4) w{p}(r)=A{p}J0(γ{p}r)+B{p}Y0(γ{p}r)+ (5) 式中:J0和Y0为零阶第一类和第二类Bessel函数;I0和K0为零阶第一类和第二类修正Bessel函数。 对于未覆盖区R{p=1},为确保圆心位置位移函数是有限的,系数B{1}和M{1}应为0,其解简化为 w{1}(r)=A{1}J0(γ{1}r)+C{1}I0(γ{1}r) (6) 单层区与双层区连接位置的结构连续性需要满足以下边界条件[17],主要包括: (1) 位移连续性 (7) (2) 坡度连续性 (8) (3) 弯矩连续性 (9) (4) 剪力连续性 (10) 此外,基底层外边缘被夹紧,表示为 (11) 将边界条件式(7)~式(11)分别代入振型函数式(5)和式(6)中,可得8m+2个齐次方程,与振型函数式(5)中包含得8m+2个未知参数A{p},B{p},C{p}和M{p}一一对应。将该8m+2个方程组写为矩阵形式 M(γ{p})·u=0 (12) 为了获得非平凡解,系数矩阵M(γ{p})的行列式必须为0 |M(γ{p})|=0 (13) 该式为高度非线性超越方程。 固有频率ω和γ{p}之间的关系 (14) 经分析,固有频率ω是矩阵方程式(13)中唯一未知量,可通过迭代寻根法求解[18]。将得到的ω代入方程(12)求解得到模态振型参数u。 轴对称振动模式圆盘的位移分量为[19] (15) 线性弹性理论下极坐标系中应变分量为 (16) 根据胡克定律,未覆盖区应力分量为 (17) 覆盖区应力分量表示为 (18) 热弹性耦合[20]导致圆板在简谐振动时产生简谐温度场,圆板中性面不受压缩或拉伸,保持在平衡温度T0。基底层和镀层的温度场增量可写为 (19) 根据薄板热弹性耦合理论,沿z轴的应变为 (20) 由于体积应变是产生温度梯度的根源,因此圆板的总体积应变为 (21) 热弹性圆板中的热传导方程为[21] (22) (23) 微谐振器采用真空超低真空封装可减少气体阻尼,其上下表面处于绝热态,热边界条件表示为 (24) 此外,磁控溅射镀膜工艺可保证基底层与镀层原子级别的结合,可假设界面处热传导是理想态,即温度和热通量连续 (25) 热传导方程式(22)本质上属于非齐次偏微分方程。为求解此方程,首先应求解其齐次形式 (26) 式中,α=κ/CV为材料的热扩散系数。 对于双层区域R{2},R{4}…,R{2m},采用分离变量方法求解,式(26)解可设为[22] (27) 将式(27)代入式(26)得 (28) 根据热边界条件式(24),可设 (29) 热边界条件式(24)和式(25)代入式(29)可得 (30) (31) 为求解式(30),其行列式应为0 (32) 式(32)化简后可得超越方程 (33) (34) 对于未覆盖区域R{1},R{3}…,R{2m+1},其本质是均质单层板。热传导控制方程式(22)退化为 (35) 根据热边界条件式(24), 式(35)的解设为 (36) (37) 时间变量函数Γ[j](t)的解为 (38) (39) 至此,热传导的特征函数和特征值全部求解完毕。 (40) 式中,格林函数为 (41) (42) 未覆盖区域温度场函数式(19)的解为 (43) 式中,格林函数为 (44) (45) 将格林函数式(41)和式(44)和热源项式(23)代入式(40)和式(44),温度场函数化简后可得 (46) (47) (48) 温度场函数式(46)的虚部为 (49) 根据Bishop等[23]之前提出的计算多层板热弹性阻尼的框架,针对不规则复杂结构,本文提出将将整体结构划分为若干规则子区域的新思路。依据能量法,热弹性阻尼可由式(50)求得 (50) 式中:ΔW{p}为一个周期的子区域能量损失;Wmax为存储的最大应变能。子区域耗散项ΔW{p}可通过式(51)计算 (51) 将应力本构式(17)、式(18)和温度场虚部式(49)代入式(51),化简后得到 (52) 式中, (53) (54) (55) 一个振动周期内总能量损失为 (56) 在一个振动周期中,圆板中存储的最大势能为 (57) 式中, (58) 本文所有积分形式的结果均是显式的。根据热弹性阻尼的定义,利用式(56)和式(57)得到热弹性阻尼解析解为 (59) 式中,参数ψ{p} (60) 以及热弛豫时间常数为 (61) 只保留第一项(n=1)可得热弹性阻尼简单模型 (62) 式中,热弛豫时间常数为 (63) 表1列出了非完全覆盖多镀层微圆板谐振器TED的完整模型和简单模型表达式。 表1 非完全覆盖多镀层微圆板谐振器热弹性阻尼完整模型和简单模型表达式Tab.1 Comparison of the full model, the simple model of TED 为便于分析,将结构参数进行无参化设置: fhk=hk/hs——镀层k与基层s厚度比; fpk=r[2k-1]/rs——镀层k内半径r[2k-1]与基层半径rs位置比; frk=(r[2k]-r[2k-1])/rs——镀层k外半径r[2k]与内半径r[2k-1]之差与基层半径rs半径的比; fαk=αk/αs——fαk代表镀层k热扩散率αk与基层s热扩散率αs之比。 本文设定基底圆板几何参数保持不变,半径rs=500 μm,厚度hs=10 μm。表2给出了基底层和镀层物理参数。 表2 材料物理参数Tab.2 Material physical coefficients 可从两方面验证本模型有效性。首先,完全覆盖双层圆板是非完全覆盖双层圆板的特殊情况。以覆盖有一个镀膜的微圆板谐振器为例,结构示意如图2所示。假设r{1}=0和r{2}=rs,当前TED模型可完全退化为完全覆盖双层微圆板谐振器模型。 其次,可利用商业有限元软件ANSYS进行验证。为减少计算量,采用8节点二维轴对称单元plane223。进行网格无关性验证后,将网格尺寸设置为小于0.5 μm。沿圆板厚度方向施加均布力F0sin(ωt),F0= 0.1 MPa。图2给出了微圆板谐振器的有限元模型、谐响应分析后的振型与温度场云图。 图2 有限元模型、谐响应分析后的振型与温度场云图Fig.2 FEM,mode shape and temperature field by the harmonic response analysis of circular microplate resonators 图3给出了位置比fp1=0.2,半径比fr1=0.6,厚度比fh1= 0.1时Ag/Si微圆板谐振器TED频率谱。同样给出了有限元结果作为对比,验证了本模型的有效性。此外,在低于Debye峰对应的临界频率,即f≤1.1×106Hz,简单模型(n=1)与n=15时的TED值误差小于5%。但随着频率变大,其误差逐渐增大,简单模型不再适用。n=10与n=15之间的误差小于5%,因此完整模型取n=15即可保证足够的精度。 图3 位置比fp1=0.2、半径比fr1=0.6、厚度比fh1=0.1时Ag/Si微圆板谐振器TED频率谱Fig.3 TED frequency spectra of Ag/Si circular microplate resonators in the case of position ratio fp1=0.2, radius ratio fr1=0.6, thickness ratio fh1 = 0.1 图4分析了fr1=1和fh1=1时SiO2/Si微圆板中TED频率谱的收敛性。fr1=1表示基底层Si圆板被镀层SiO2完全覆盖。从图4中可看出,频率谱中可观察到两个显著的Debye峰。若使用简单模型(n=1)计算则高频率处Debye峰将被忽略,存在严重误差。 图4 半径比fr1 = 1、厚度比fh1=1时SiO2/Si微圆板谐振器TED频率谱Fig.4 TED frequency spectra of SiO2/Si circular microplate resonators in the case of radius ratio fr1=1, thickness ratio fh1=1 本节从镀层的厚度、半径出发分析简单模型的适用范围。图5给出了不同厚度比fh1=h1/hs的Ag/Si圆板TED频率谱图。从图5可看出,随着fh1减小,模型收敛性逐渐增大。当fh1=0.01时,TED简单模型与完整模型的值相对误差小于2%。此时,可用简单模型代替完整模型进行快速计算,以降低计算量。 图5 不同厚度比fh1=h1/hs的Ag/Si圆板TED频率谱Fig.5 TED frequency spectra of Ag/Si microplates with different thickness ratio fh1=h1/hs 图6分析了不同厚度比fh1=h1/hs的SiO2/Si圆板TED频率谱特性。可注意到,只有fh1=1时出现了双峰现象,随着fh1减小,低频峰逐渐消失,但高频峰的峰值逐渐增大。可知,SiO2层可降低高频峰值,但在低频处会增大TED值。 图6 不同厚度比fh1=h1/hs的SiO2/Si圆板TED频率谱Fig.6 TED frequency spectra of SiO2/Si microplates with different thickness ratio fh1=h1/hs 图7给出了不同半径比fr1=(r[2k]-r[2k-1])/rs的Ag/Si圆板中TED频率谱值。从图7可看出,随着fr1减小,频率谱峰值逐渐减小,收敛性也逐渐变快。当fr1=0.2时,可用简单模型代替完整模型快速估算TED值。 图7 不同半径比fr1=(r[2k]-r[2k-1])/rs的Ag/Si圆板中TED频率谱Fig.7 TED frequency spectra of Ag/Si microplates with different radii ratio fr1=(r[2k]-r[2k-1])/rs 图8研究了不同半径比(r[2k]-r[2k-1])/rs的SiO2/Si圆板中TED频率谱特性。从图8可知,随着fr1逐渐变小,低频峰值逐渐减小,但高频峰值逐渐增大。直到fr1=0.2时,低频峰消失。同图7一样,此时用简单模型计算TED值即可保证较高精度。 图8 不同半径比(r[2k]-r[2k-1])/rs的SiO2/Si圆板中TED频率谱Fig.8 TED frequency spectra of SiO2/Si microplates with different radii ratio (r[2k]-r[2k-1])/rs 图9分析了Si/DLC/SiO2圆板TED频率谱特性。DLC (diamond-like carbon)是类金刚石典型特征的一类材料的统称。镀层1(Si)、镀层2(DLC)与基底层(SiO2)的厚度比分别为fh1=1,fh2=0.4;位置比分别为fp1=0,fp2=0.8;半径比为fr1=0.8,fr2=0.2。 如图9所示,TED频率谱中存在3个显著的Debye峰。如果使用简单模型计算,将丢失第2和第3个峰值,造成严重误差。因此,此时不可使用简单模型计算TED。此外,当n=20计算时,可观察到2个Debye峰,第3个Debye峰丢失。只有使用完整模型取n=100时,才可捕捉到3个Debye峰。n=100时TED值与n=400时的结果几乎完全重合。 图9 Si/DLC/SiO2圆板的TED频率谱特性曲线。厚度比为fh1=1,fh2=0.4;位置比为fp1=0,fp2=0.8;半径比为fr1=0.8,fr2=0.2Fig.9 TED frequency spectra behaviors of Si/DLC/SiO2 in circular microplates with the thickness ratio fh1=1, fh2=0.4, position ratio fp1=0, fp2=0.8 and radii ratio fr1=0.8, fr2=0.2 本文首次提出一种可计算具有多个非完全覆盖镀层微圆板谐振器TED的通用计算框架。根据分析结果,概括出以下几个重要结论: (1) 该解析模型仅用于微薄板谐振器,可退化为完全覆盖双层圆板模型,与有限元计算结果吻合很好。 (2) 该解析模型收敛性随厚度比和半径比减小而逐渐增大。在fh1≤0.01或fr1≤0.2时可用简单模型替代完整模型计算TED值,以减少计算量。 (3) 在Si/DLC/SiO2微圆板的TED频率谱中发现3个显著的Debye峰。此时,只能使用完整模型计算,使用简单模型会造成严重误差。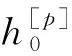
C{p}I0(γ{p}r)+M{p}K0(γ{p}r)1.2 温度场求解






1.3 热弹性阻尼模型
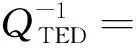


2 模型分析与讨论

2.1 模型验证与收敛速度分析



2.2 简单模型和完整模型的对比分析




2.3 具有2个局部镀层的微圆板TED频率谱分析

3 结 论

