基于多域特征的BA-KELM微型电机故障检测

郭明军， 李伟光， 赵学智， 张欣欣

(1. 广西科技大学 机械与汽车工程学院，广西 柳州 545616； 2. 华南理工大学 机械与汽车工程学院，广州 510640)

电机自19世纪被发明以来，逐渐应用到工业生产、智能家居、汽车行业等领域，并深刻地改变着人们的生产和生活方式[1]。电机作为各类机电设备的核心动力部件，如何确保其可靠稳定连续运行事关企业经济效益及人民财产安全，故需对其运行状态进行监测与诊断。由于良品电机与故障电机的运行状态存在明显差异，通过检测电机运行过程中的振动信号、声音信号及电流信号等特征信号，可以实现电机的故障诊断。

王博磊等[2]对电机振动信号进行集成经验模态分解(ensemble empirical mode decomposition,EEMD)处理得到包含不同频率成分的本征模态分量(intrinsic mode fuction,IMF)，并计算出各分量的能量比及不同频段能量比来构造特征向量，通过支持向量机(support vector machine, SVM)实现电机故障的识别。蔡少辉[3]通过对电机振动信号进行Hilbert包络谱分析，根据振动信号中故障频率对应的边带成分实现故障定位。李俊卿等[4]提出利用SVD及改进小生境遗传算法对电机定子电流的谐波分量进行分析，成功识别出双馈异步电机转子的匝间短路故障。何玉灵等[5]提出利用最大相关解卷积算法来增强电机振动信号中的故障特征，成功实现了发电机运行状态的识别。李俊卿等[6]分别从失电残压和扩展Park变换中提取故障特征，然后利用支持向量机分别对两种特征量进行初步诊断，最后基于D-S证据理论对诊断结果进行融合得出最终结论，有效提高了风机定子匝间短路故障诊断的精度。Yan等[7]提出基于小波分析和注意机制的电机故障诊断算法，通过小波分析去除电机振动信号的高频噪声，并以分解后的频带作为输入，采用卷积神经网络融合数据的频带特征，利用双向门控环路单元融合时间序列特征，然后,注意利用注意力机制自适应集成不同时间点的特征，最后，通过分类器识别实现电机故障诊断与预测。王栋悦等[8]将负序电流差与定子径向振动信号的二倍频分量分别用于训练支持向量机分类器，然后基于D-S证据理论进行融合作为最终的诊断结果，所提方法诊断精度比基于单一信号的方法高。范万里[9]将利用小波分析对机车牵引电机振动信号进行去噪，以不同特征频率的归一化能量比为输入训练BP神经网络，有效识别了电机故障类型。李强等[10]以小波包提取得到的异步电机故障特征向量矩阵为输入，并利用改进粒子群算法对BP神经网络模型进行优化，可以更加快速可靠的实现电机故障诊断。

近年来，极限学习机(extreme learning machine, ELM)因较传统BP神经网络具有更好的泛化性能，且能在保证学习精度的前提下情况下具有更好的学习效率，而被广泛应用于脉动风速预测[11]、旋转机械故障诊断[12]、滚动轴承故障诊断[13]等领域。ELM[14]的最大特点是可以随机设定输入与隐含层之间的连接权重，且设定后不需要像BP神经网络那样不断地反向调整，大大减少了计算量。核极限学习机[15](kernel based extreme learning machine，KELM)是基于ELM并结合核函数所提出的改进算法，KELM 能够在保留 ELM 优点的基础上提高模型的预测性能。

鉴于目前有关电机故障诊断的研究多聚焦于大型电机，而有关微型电机的故障诊断则鲜有报道。因此，本文着重研究微型电机的故障诊断问题，提出一种基于KELM及电压信号多域特征的微型电机故障诊断模型：采用EEMD对采集到的电机电压信号进行处理，分别计算各IMF的能量比及样本熵特征并与电压信号的时域及频域特征构成电机信号多域特征集，并以此为基础建立基于KELM的电机故障诊断模型。

1 微型电机电压信号检测

微型电机检测平台如图1所示。将微型电机与定值电阻串联，并由深圳迈斯泰克电子有限公司生产的DP305型号直流稳压电源供电，采用研华PCI-1742U数据采集卡及LabVIEW驱动程序实现电压信号的实时采集。

图1 微型电机检测平台Fig.1 Micro motor testing platform

试验用微型电机(如图2所示)由合作单位提供，包括良品电机和故障电机各100个，型号为R30-FT-50079w。电机大壳总长为30.8 mm，端子间距为18.3 mm，电机直径为24.4 mm。

图2 待测微型电机样品Fig.2 Sample of micro motor to be tested

利用图1所示的检测装置，对标记好类别的良品及故障电机分别进行检测，测试结果分别如图3和图4所示。

图3 良品电机电压信号Fig.3 Voltage signal of normal motor

图4 故障电机电压信号Fig.4 Voltage signal of fault motor

图3为良品电机的电压信号的时域波形及频谱图。由图3可知，良品电机电压信号呈周期性脉冲变化，即在一个周期内波峰与波谷连接处电压值出现急速下降。而从良品电机电压信号的频谱图中可以看出，基频70.8 Hz的幅值最大(约为0.284 2)，除基频外还存在高次谐波成分，频谱成分相当丰富。图4为故障电机的电压信号的时域波形及频谱图。由图4可知，故障电机电压信号与图3中的良品电机一样也表现出周期性脉冲变化，两者的时域波形特征相似，但从频谱图中可以看出，故障基频减小为65.92 Hz而幅值约降为良品电机的一半(幅值约为0.153 9)，且故障电机电压信号中出现了良品电机中不存在的频率，这些频率成分分布更加密集。由此说明，当微型电机发生故障时，其电压信号的时域波形会发生明显的滞后，而其频谱成分也会产生相应的变化，因此，可以电机电压信号的时域特征及频域特征为特征量来进行故障诊断。

2 多域特征提取及筛选

2.1 时域及频域特征

本文中需要提取的特征指标如表1所示。表1包括9个时域特征及4个频率特征，其中：ft1～ft6为有量纲时域特征指标；ft7～ft9为无量纲时域特征指标；ft10～ft13为频域特征指标。图3和图4中的良品及故障电机信号的时域及频域特征计算结果分别如表2和表3所示。

表1 信号的时域及频域特征Tab.1 Time and frequency domain features of signal

表2 良品电机信号的时域及频域特征计算结果Tab.2 Time and frequency domain features of normal motor signal

表3 故障电机信号的时域及频域特征的计算结果Tab.3 Time and frequency domain features of fault motor signal

2.2 时频域特征

由于本文中电机电压信号是具有明显的非线性非平稳特征，为了更好的刻画电机的变化规律，采用EEMD算法处理电机信号，得到包含不同时频域特征的IMF，然后分别计算各分量的能量比及样本熵特征。

2.2.1 能量比

由前文分析可知，良品电机与故障电机电机信号的频谱特征存在差异，信号在不同频率处的幅值大小明显不同，而幅值差能够表征电机的故障状态。假设原始信号的能量为E0，Ej为第j个IMF的能量，则能量比定义为En。

(1)

(2)

2.2.2 样本熵

样本熵可以量化表达非线性时间序列，适合旋转机械信号的分析。假设时间序列的长度为N，维数为m，相容极限为r，则样本熵的计算过程为：

将原始信号重构为m维矢量

X(i)=[x(i),x(i+1),…,x(i+m-1)]

(3)

式中，i=1,2,…,N-m+1。

计算任意两个矢量之间的距离

(4)

(5)

(6)

(7)

在实计算中N为有限值时，样本熵可以由式(8)估算

(8)

2.2.3 时频特征筛选

对电机信号进行EEMD处理可以得到多个IMF，由于每个分量包含的特征信息量不一样。因此本文采用相关系数cc来衡量各IMF与原始电压信号的相关程度，并且设定阈值ccr为0.5，筛选出相关系数大于ccr的前3个分量进行能量比和样本熵特征的计算。

(9)

式中：cov(i,j)为序列i,j之间的协方差；Var[i],Var[j]为对应序列的方差。

为了说明时频特征的基本筛选过程，分别对图3及图4中的信号进行EEMD分解，结果分别如图5和图6所示。

图5 良品电机电压信号EEMD分解结果Fig.5 EEMD result of voltage signal of normal motor

图6 故障电机电压信号EEMD分解结果Fig.6 EEMD result of voltage signal of faultnormal motor

分别计算图5中各IMF的相关系数，结果如图7所示。由图7可知，第1、第6、第7个IMF的相关系数都在阈值之上，因此选IMF1，IMF6，IMF7来计算样本熵和能量比特征(结果列于表4中)。由于不同良品电机的信号特征相似，故对于其余的良品电机均按此选此3个IMF来计算相应的时频特征。

图7 良品电机的各IMF相关系数计算结果Fig.7 Correlation coefficient of each IMF components of the normal motor

分别计算图6中故障电机信号的各IMF的相关系数，结果如图8所示。由图8可知，第1、第6、第7个IMF的相关系数都在阈值ccr之上，因此选IMF1，IMF6，IMF7来计算样本熵和能量比特征(结果列于表4中)。由于不同故障电机的信号特征相似，故对于其余的故障电机均选此3个IMF来计算相应的时频特征。

图8 故障电机的各IMF相关系数计算结果Fig.8 Correlation coefficient of each IMF components of the fault motor

表4 电压信号的时频特征计算结果Tab.4 The calculation results of voltage signal time-frequency characteristics

3 微型电机故障诊断方法及流程

3.1 KELM基本原理及参数优化

ELM在训练前通过随机初始化连接权重及阈值参数，不需要像BP神经网络那样不断地反向调整，大大减少了计算量。而将核函数与ELM相结合的改进模型KELM，在保留 ELM 优点的基础上能极大提高模型的预测性能。

本文中KELM模型中的核函数采用RBF核函数，其表达式为

(10)

式中，γ为核系数。

KELM的目标函数为

(11)

式中:h(x)，H为隐藏层输出;C为惩罚系数;Y为期望输出。

fi=fmin+(fmax-fmin)*α

(12)

(13)

(14)

通过局部搜索随机产生新的局部解

对于《印度之行》这部小说，不同的文学评论家持有不同的看法。但是多数人都赞同洛奇的看法：《印度之行》不仅具有现实主义小说的特点，还善用象征手法，也可称之为一部象征主义小说。另外，《印度之行》这部作品拥有丰富的象征意蕴，不仅书名和人名具有象征性，而且小说的结构也具有一定的象征性。

xnew=xold+εAt

(15)

根据回声定位原理调整更新声波的响度和频率参数

(16)

(17)

式中:λ∈(0,1)为声波衰减系数;μ>0为脉冲频度系数。

3.2 电机故障诊断试验

试验数据来源于自主搭建的微型电机检测平台(见图1)，测试对象为良品电机与故障电机各100个，按照3∶2的比例划分为训练集和测试集，即训练集包含60个良品电机样本和60个故障电机样本，测试集包含40个良品电机样本和40个故障电机样本。图9为电机故障诊断流程。

图9 电机故障诊断流程Fig.9 The process of motor fault diagnosis

步骤1样本集构造。对采集到的电机信号，分别计算其时域、频域及时频域特征，并由计算得到的每个信号的9个时域特征、4个频率特征及6个时频域特征组成维度为200×19的多域特征集并进行归一化处理；然后，按照3∶2的比例划分为训练集和测试集，即训练集包含60个良品电机样本和60个故障电机样本，测试机包含40个良品电机样本和40个故障电机样本。

步骤2模型训练及参数优化。以训练集的错误率为适应度函数，采用BA算法优化KELM模型的核系数及惩罚因子(γ,C)，结果如图10所示。由图10可知，适应度值在整个迭代过程中都为0.125，说明采用BA算法在第一次迭代中就获得了最优解，此时最优参数组合为(γbest,Cbest)∶(394.170 0,1.284 2)。保持其余参数不变，代入上述最优值即可得到优化的KELM模型。

图10 BA算法优化KELM参数的适应度曲线Fig.10 The fitness curve of KELM parameters optimized by BA algorithm

步骤3模型测试。分别以训练集和测试集样本为输入，对BA-KELM的优化模型进行测试，结果如图11所示。由图11可知，训练集准确率达到100%，测试集的准确率为98.75%，说明BA-KELM优化模型的泛化性能很好。

图11 基于BA- KELM优化模型的电机诊断结果Fig.11 Diagnosis results based on BA-KELM optimization model

为了进一步说明此问题，将数据样本按照不同的比例进行划分，然后按照图9中的步骤进行电机故障诊断，结果列于表5中。由表5可知，在不同的样本集划分方式下，测试集的准确率最低值都达到96.67%，进一步说明了BA-KELM优化模型的泛化性能很好。

表5 不同样本集划分比例下的诊断结果Tab.5 Diagnosis results under different proportion of sample set partition

3.3 对比试验

采用相同的数据集对BP神经网络、SVM、ELM及KELM模型进行训练和测试作为对比，10次重复性试验的诊断结果(以准确率为评价指标)如图12所示。由图12可知，5种模型中BA-KELM在各次试验中的准确率都是最高的98.75%，BA-KELM，KELM，ELM，BP，SVM模型的平均准确率分别为98.75%，95%，94.5%，92.67%，53.75%。

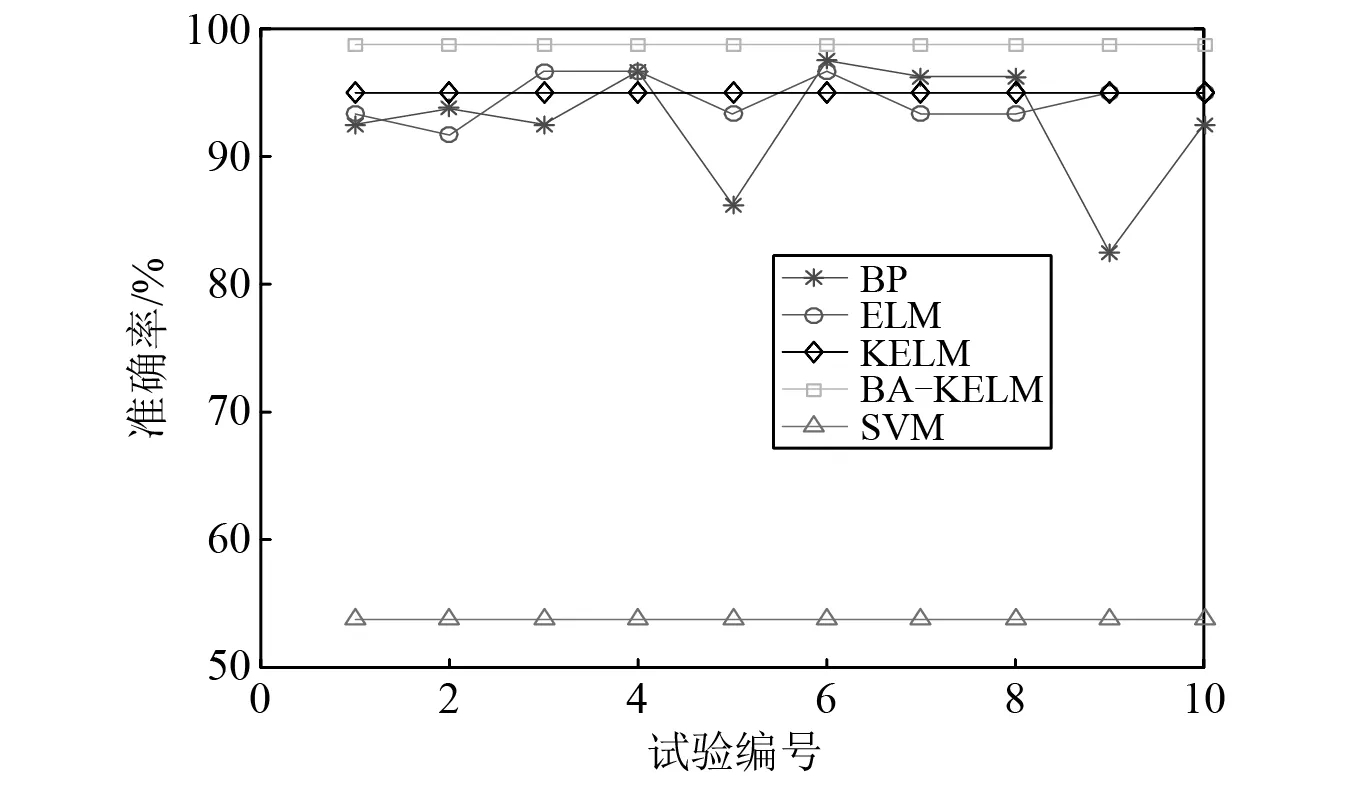
图12 不同模型电机故障诊断结果Fig.12 Motors fault diagnosis results of different models

4 结 论

本文对微型电机故障检测方法进行了研究：搭建了微型电机信号检测平台，实现了微型电机电压信号的监测与采集。为了实现电机故障检及提高诊断精度，克服传统基于单域特征诊断方法的缺陷，构造包含电机信号的时域特征、频域特征及时频域特征的多域特征集(其中时频域特征是用基于相关系数准则筛选EEMD处理电机信号得到的IMF计算得到的能量比和样本熵特征)，并采用蝙蝠算法对KELM模型进行参数优化。试验结果表明，基于BA-KELM模型的准确率达98.75%，且在不同样本集划分方式下的测试结果都很好，说明了该方法的泛化性能优秀。对比试验结果表明，BA-KELM模型的诊断性能比BP神经网络、ELM及未经参数优化的KELM模型更好。

本文研究为微型电机故障检测提供了一种可行方案，极大弥补了该领域的空白。下阶段将在本阶段的微型电机故障检测的基础上，进一步研究不同故障类型微型电机的模式识别问题。