考虑剪切变形的连续钢-混组合梁动力特性分析

孙琪凯， 张 楠， 刘 潇

(北京交通大学 土木建筑工程学院，北京 100044)

连续钢-混组合梁(以下简称“连续组合梁”)具有刚度较大、跨越性能好等优势，而常被应用于公路、铁路桥梁建设中。其一般由混凝土子梁和钢梁两部分组成，并通过剪力键传递两者之间的剪力。由于剪力键的柔性特性造成连续组合梁运动时钢梁和混凝土子梁之间产生相对剪切滑移，使得其动力性能变得比单一材料的连续梁更为复杂[1-3]。目前，关于连续组合梁动力性能研究的文献很少[4-5]。且其分析模型中未考虑剪切变形的影响或考虑了剪切变形但假定子梁剪切角相等。这两种假定均会高估组合梁的截面抗弯刚度，从而高估其自振频率[6]。因此，提出一种子梁分别为独立变形的Timoshenko梁单元的连续组合梁动力性能分析模型是十分必要的。

目前，组合梁试验研究主要有组合梁的动力响应[7-8]、剪力键疲劳性能[9-11]等方面。理论研究方面，目前发展出了Euler-Bernoulli组合梁理论(EBT组合梁)[12-15]、Timoshenko组合梁理论(TBT组合梁)[16-18]以及高阶组合梁理论(HBT组合梁)[19-21]等。EBT组合梁不考虑剪切变形和转动惯量的影响，使得组合梁频率计算结果大于实际结果，特别是对短粗梁和组合梁的高阶频率。Xu等和Lin等均考虑了剪切变形和转动惯量的影响，但假定钢梁和混凝土子梁具有相同的剪切角，一定程度上提高了组合梁动力分析的计算精度。然而钢梁和混凝土子梁的剪切角显然是不相等的，人为假定其相等仍然会造成组合梁刚度的高估。因此Nguyen等基于子梁独立转角假定，推导了组合梁的运动微分方程并求解单跨组合梁的自振特性。该假定更加符合组合梁的运动状态，提高了计算精度。HBT组合梁理论是假定多个未知量，使组合梁的位移场函数更加符合实际情况；基于能量原理并采用有限元的方法，分析组合梁的动力性能。其主要的优点是能够分析组合梁的截面应力分布，但是由于假定的未知参数很多，造成计算分析时工作量较大。综合以上讨论，进行连续组合梁动力性能分析时，应基于Timoshenko梁理论且假定子梁的剪切角是相互独立的。从而提高计算模型的精度。

本文拟基于Timoshenko梁理论，考虑剪切变形和界面滑移的影响，提出一种连续组合梁动力分析模型。假定混凝土子梁和钢梁分别具有独立的剪切角，使其与连续组合梁的实际运动状态更符合，从而提高其计算精确。并通过分析边中跨比、跨高比和剪切变形等因素对连续组合梁自振特性的影响，给出可以忽略剪切变形、剪切滑移影响的条件。

1 计算理论

1.1 振型函数

本文研究的对象是线弹性、平直连续组合梁，如图1所示。基本假定如下：①混凝土子梁和钢梁分别独立的满足Timoshenko梁单元假设，考虑剪切变形而忽略转动惯量的影响；②本文仅研究组合梁的平面内运动，且满足小变形假设；③混凝土子梁在横向上(z方向)与钢梁不发生掀起脱离，而只能产生水平向(x方向)的相对剪切滑移；④剪力键承担全部的剪力，忽略混凝土子梁与钢梁之间的黏结摩擦等相互作用，且界面剪切滑移量与剪力键承受的剪力成正比关系，剪力键等效为连续分布的刚度为K的弹簧。

图1 连续钢-混组合梁构造图Fig.1 Structural drawing of steel-concrete composite continuous beam

基于以上假定，Sun等已推导得到了考虑剪切变形的组合梁的运动微分方程式

(1b)

(1c)

(1d)

(1e)

(1f)

式中:EAs=EsAs；EAc=EcAc；EA=EsAsEcAc/(EsAs+EcAc)；EIs=EsIs；EIc=EcIc；EIF=EI+EAh2；GAs=ksGsAs；GAc=kcGcAc；GA=GAs+GAc；GAF=GAsGAc/(GAs+GAc)；EI=EIs+EIc；m=ρsAs+ρcAc；下标c和s分别为混凝土子梁和钢梁的材料和结构参数；hc和hs分别为混凝土子梁和钢梁中性轴到钢混交界面的距离，h为两者之和；Ei，ki，Gi，Ii，ρi和Ai(i=c,s)分别为子梁的杨氏模量、剪切形状系数、剪切模量、抗弯惯性矩、密度和横截面积。

如图1所示，为了分析连续组合梁的动力性能，把其第k个中间支座等效为反力荷载Rk(t)(k=1-n)。则连续组合梁动力问题变为承受集中荷载的简支梁动力问题。等效的支座反力荷载可以写为

(2)

式中：ω为连续组合梁的自振频率；i为虚数单位；δ(x-xi)为Dirac函数，其表达式为

(3)

式(1)可采用分离变量的方法进行求解，即假定

w(x,t)=φ(x)eiωt

(4)

式中，φ(x)为组合梁的振型。

把式(2)和式(4)代入式(1a)可得

(5)

对式(5)的等号的两端进行Laplace变换，可得

[s8-(η31-η32mω2)s6+(η21-η22mω2)s4+η1mω2s2-η0mω2]L[φ]=

[s7-(η31-η32mω2)s5+(η21-η22mω2)s3+η1mω2s]φ(0)+

[s6-(η31-η32mω2)s4+(η21-η22mω2)s2+η1mω2]φ′(0)+

[s5-(η31-η32mω2)s3+(η21-η22mω2)s]φ″(0)+

[s4-(η31-η32mω2)s2+(η21-η22mω2)]φ‴(0)+

[s3-(η31-η32mω2)s]φ(4)(0)+[s2-(η31-η32mω2)]φ(5)(0)+

(6)

式中:φ(k)(k=4～7)为对x的k阶求导；φ(7)=d7φ/dx7；s为拉普拉斯变换参数。

式(6)可以写为

(7a)

(7b)

对于分母，即

s8-(η31-η32mω2)s6+(η21-η22mω2)s4+

η1mω2s2-η0mω2=0

(8)

其可以写为关于χ=s2的一元四次方程式，即

χ4+a3χ3+a2χ2+a1χ+a0=0

(9a)

a0=-η0mω2,a1=η1mω2

(9b)

a2=η21-η22mω2,a3=η32mω2-η31

(9c)

由孙琪凯等的研究可知其有一个负根(χ4<0)和3个正根(χ1，χ2和χ3>0)，则由费拉里法可得式(9a)的解为

(10a)

(10b)

p2=a3κ1-a1

(10c)

式中，κ1为式(11)的任意实数解。

8κ3-4a2κ2-(8a0-2a1a3)κ-

(11)

则式(8)的8个根可以写为

(12)

采用查表法并利用Laplace变换的位移定理，做式(7)的逆Laplace变换，可得

φ(x)=A1sinh(λ1x)+A2cosh(λ1x)+

A3sinh(λ2x)+A4cosh(λ2x)+

A5sinh(λ3x)+A6cosh(λ3x)+

A7sin(λ4x)+A8cos(λ4x)-

(13a)

(13b)

(13c)

式中：Ai(i=1～8)为与边界条件有关的待定系数；H(x-xk)为赫维赛德函数，其表达式为

(14)

一般的，工程中较常见的边界条件有悬臂、两端简支、固支-简支、两端固支以及连续梁等。对于四种边界条件的单跨梁，Rk=0，式(13a)退化为仅含Ai(i=1～8)等8个待定系数的阵型函数，与孙琪凯等研究中的结果相同。代入边界条件，并令Ai(i=1～8)的系数矩阵的行列式为0，即可得到各边界条件下，钢-混组合梁的频率。

1.2 简支梁自振特性

对于简支梁和连续梁，其梁端边界条件均为

(15)

把式(15)和Rk=0代入式(13)，并令Ai(i=1～8)的系数矩阵的行列式为0，即可的

(16b)

(16c)

(16d)

(16e)

(16f)

(16g)

式(16)中当且仅当sin(λ4L)=0时才成立，即λ4=nπ/L。因此简支钢-混组合梁的振型为

(17)

把λ=±λ4i=±nπ/L代入式(5)即可得钢-混组合梁的自振圆频率ωn显式表达式为

(18a)

(18b)

(18c)

(18d)

(18e)

1.3 连续梁自振特性

把连续梁的梁端边界条件式(15)代入式(13)可得待定系数Ai(i=1～8)如下

A2=A4=A6=A8=0

(19a)

(19b)

因此，式(13)变为

(20)

再由连续梁中间支撑的边界条件φ(xk)=0，可得关于中间支座反力的n个方程，如下

(21)

对式(21)进行讨论，如下：

(1)对于跨径为n×L的等跨度的连续钢-混组合梁，当其振型为反对称模式时，中间支座反力恒为0，即Ri=0恒成立。此时，等跨连续梁的振动特性与同跨径的简支组合梁相同。两跨等跨连续组合梁的情况，如图2所示。因此，等跨连续梁的反对称模态对应的自振频率可由式(18a)求得。即n跨等跨连续组合梁的第[1+(k-1)n]阶自振频率与跨径为L的简支组合梁的第k阶自振频率相等。

图2 组合梁振型示意图Fig.2 Vibration mode diagram of steel-concrete composite beam

(2)对于其他工况，由于Ri(i=1～n)不全为0，因此其系数矩阵行列式为0，即detN=0，即可求得连续梁的自振频率及中间支座反力向量{R}。把自振频率和向量{R}代入式(13)，即可得到连续钢-混组合梁的振型。

采用MATLAB软件编制本文方法计算程序，具体计算流程如下所示

步骤1对于跨径为n×L的等跨连续梁，其第[1+(k-1)n]阶自振频率与跨径为L的简支组合梁的第k阶自振频率相等，可由式(18a)求得。

步骤2对于等跨连续组合梁的其他模态以及不等跨连续梁。首先，假定一个自振频率增量Δω，设ωj=ωj-1+Δω，且ω1=0。

步骤3把ωj代入式(8)，计算λi(i=1～8)；然后代入式(21)中的矩阵N，得到ωj对应的矩阵Nj。

步骤4求解矩阵Nj的行列式，detNj。若detNj×detNj-1<0，则设置Δω=-Δω/2。

步骤5收敛性判断。当|detNj|<规定误差值后，ωj即为所求；否则，令ωj+1=ωj，并重复步骤2～步骤5。

2 算例验证

本章以1根两跨连续钢-混组合试验梁为例，验证本文中提出的理论，试验梁的构造图如图3所示。试验梁全长为12.4 m，跨径为2×6.0 m。若假定剪力钉均匀分布，则剪力键刚度K为1 398 MPa；若沿梁长按照剪力键疏密度不同进行分段，则试验梁可分为(1.05+4.3+1.7+4.3+1.05)m，相应的剪力键刚度值为(2 247+1 002+2 353+1 002+2 247)MPa。

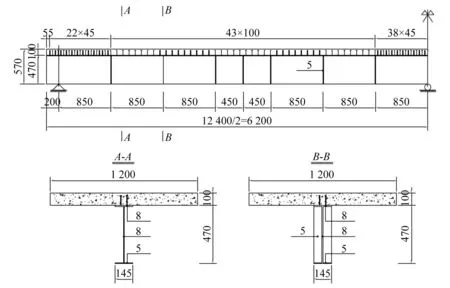
图3 试验梁构造图 (mm)Fig.3 Structural drawing of experimental beam (mm)

试验梁的材料参数见表1所示。

表1 梁材料参数Tab.1 Material parameters of composite beam

在试验梁第一跨的跨中布置测点，测试其在脉动荷载作用下的加速度，并通过自谱分析获得连续组合梁的自振频率。测试工作照及测试结果如图4所示。

图4 室内试验Fig.4 Experiment in the laboratory

使用有限元软件ANSYS建立该连续钢-混组合梁的有限元模型，如图5所示。模型中分别采用采用SOLID65单元、SHELL63单元和COMBIN39三维弹簧单元模拟组合梁的混凝土子梁、钢梁和剪力键，并且混凝土子梁和钢梁之间竖向耦合但纵横向为弹性约束。

图5 计算模型Fig.5 Calculation model

表2为本文理论结果、测试结果、ANSYS计算结果、EBT梁理论结果(Fang等)和子梁相同剪切角假设的TBT梁理论结果(Wang等)的对比情况。括号内数字为文献中方法相对于本文方法的误差。ANSYS剪力键实布表示按照剪力键实际布置疏密度进行分段设置剪力键刚度；剪力键均布表示假定剪力键沿梁长均匀分布。该两跨连续梁的本文理论推导过程见附录。

表2 试验梁自振频率分析结果对比表Tab.2 Comparison of eigenfrequencies obtained by different methods for experimental beam

ANSYS剪力键均布假定的计算结果中，前5阶振型云图如图6所示。

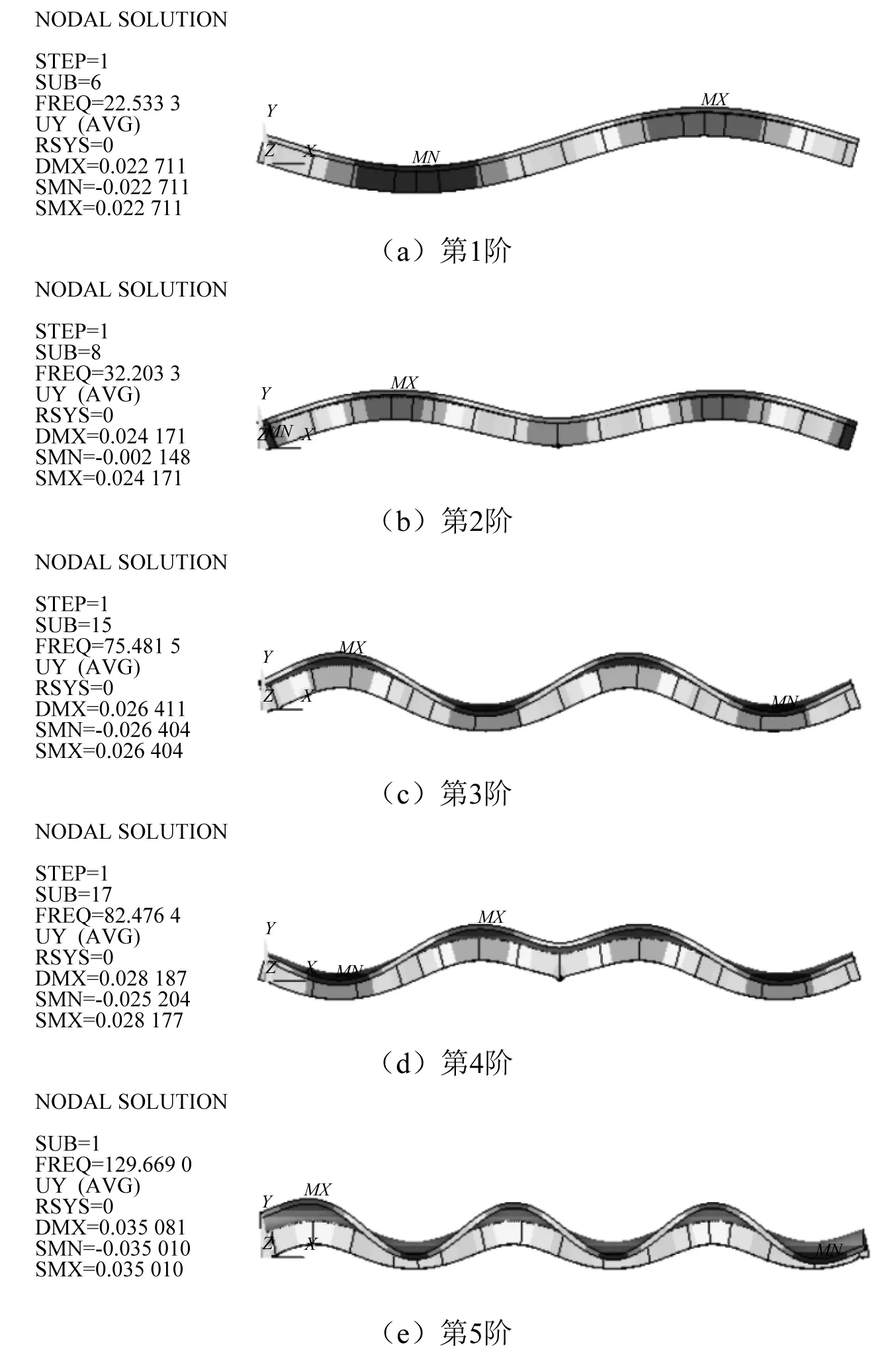
图6 前5阶振型Fig.6 The first five modes

由表2可得：

(1)本文理论计算结果与ANSYS计算结果基本一致。说明本文理论计算方法可用于分析连续钢-混组合梁动力特性的分析；两者结果均略大于测试结果，初步推断是由于试验梁的边界条件并非是理想的。

(2)ANSYS计算结果中，剪力键均布假定与剪力键实布的频率计算结果基本一致，说明本算例假定剪力键沿梁长均匀布置是合适的。

(3)相比于EBT组合梁理论模型和子梁等转角假定的TBT组合梁理论模型，本文中理论模型的计算结果更接近于ANSYS计算结果。

(4)前两种理论计算模型相对于本文计算模型的误差随着阵型阶数而增大。第1阶频率相对误差分别为3.1%(EBT模型)和2.3%(子梁等转角假定模型)，相差不大；但第5阶频率相对误差分别达到了18.1%和7.2%。说明计算连续钢-混组合梁的高阶频率时，剪切变形不可忽略且不可假定子梁转角相等。

3 剪切变形影响分析

本章以第2章中的算例为研究对象，旨在讨论剪力键刚度、跨数、边中跨比和跨高比对连续钢-混组合梁自振频率的影响。通过与Fang等研究中的EBT组合梁模型对比，说明剪切变形是否影响连续组合梁随以上三种因素的变化规律。并最终给出跨高比为何时，可忽略剪切变形的影响。

文献[22]中给出了简支钢-混组合梁的剪力键刚度对是否考虑剪切变形产生误差的影响，分析表明，剪力键刚度越大，是否考虑剪切变形产生的误差越大。对于连续钢-混组合梁，这一结论有待验证。

图7给出了两跨连续组合梁的前4阶自振频率是否考虑剪切变形产生的相对误差随剪力键刚度的变化规律。ωEBT为基于EBT组合梁理论的频率计算结果；ωTBT为本文基于TBT组合梁理论的频率计算结果。可以明显得出与简支组合梁相同的结论：频率阶数越高，剪力键刚度越大，两种理论的相对误差越明显，表明剪切变形的影响越大。

图7 前4阶自振频率误差随剪力键刚度的变化情况Fig.7 The effect of shear connector stiffness on the errors of the first four eigenfrequencies

图8给出了基于EBT组合梁理论的频率折减系数随剪力键刚度的变化情况。图9给出了基于本文TBT组合梁理论的连续钢-混组合梁的边中跨比分别为0.6，0.8和1.0时，频率折减系数随剪力键刚度的变化情况。图中，ωEBTF和ωTBTF分别为采用两种理论计算剪力键刚度为无穷大时的组合梁频率。

图8 频率折减系数与剪力键刚度的关系(EBT理论)Fig.8 The effect of shear connector stiffness on the frequency reduction factor (EBT)

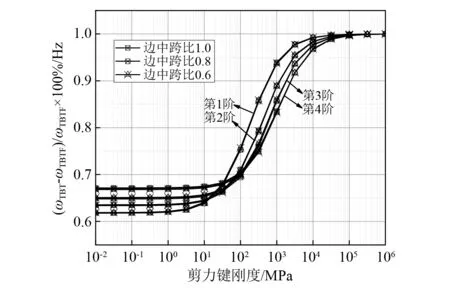
图9 频率折减系数与剪力键刚度的关系(TBT理论)Fig.9 The effect of shear connector stiffness on the frequency reduction factor (TBT)

对比图8和图9的结果可以看出：

(1)剪切变形并不影响频率折减系数随剪力键刚度的变化规律；两种理论存在相同的剪力键刚度敏感区，即在此区段内频率折减系数随剪力键刚度而迅速变化。对于第1～第4阶频率，这一区段分别约为：第1阶(100MPa

(2)当剪力键刚度大于105.0MPa后，前4阶频率的折减系数几乎为1.0。说明当剪力键刚度大于105.0MPa后，可不考虑剪切滑移的影响。

(3)剪力键刚度较小既混凝土子梁和钢梁之间约束较弱时，基于BET组合梁理论的前4阶频率折减系数趋于相同值，约为0.61；而基于TBT组合梁理论的前4阶结果并不趋近于相同值，其值均大于0.61，且阶数越高其值越大。

(4)不同边中跨比连续钢-混组合梁的频率折减系数基本一致。该结论与Fang等 (EBT组合梁理论) 的结论一致，说明剪切变形并不影响边中跨比与频率折减系数和剪力键刚度之间的关系。

在工程应用中，连续梁的第1阶是更为受关注的。综合以上结论，即n×L1的等跨连续组合梁基频与跨径为L1的简支组合梁基频相等；剪切变形、边中跨比对剪力键刚度对频率折减系数的敏感区段范围无明显影响，仅影响频率折减系数的值。因此全长为L的n跨连续组合梁的基频折减系数随剪力键刚度的变化规律与跨径为L/n的简支组合梁相同。孙琪凯等中给出了简支组合梁跨高比大于10时，剪切变形造成的基频频率误差小于5%，即基频分析时剪切变形可以忽略。因此对于全长为L的n跨连续组合梁基频分析，L/(nh)>10时，可忽略剪切变形的影响。其中h为梁截面高度。

4 结 论

本文考虑剪切变形的影响，提出了一种分析连续钢-混组合梁动力特性的新方法。通过试验梁模型对方法的适用性进行了验证，并讨论了剪切变形、剪力键刚度、边中跨比对频率折减系数的影响，主要结论如下：

(1) 本文提出的方法适用于分析连续钢-混组合梁的动力特性。并且相比于Euler-Bernoulli组合梁计算模型和子梁同剪切角假设的Timoshenko组合梁计算模型，本文的方法具有更高的计算精度。

(2) 频率阶数越高，剪力键刚度越大，剪切变形对连续钢-混组合梁频率的影响越大。

(3) 剪切变形、边中跨比对剪力键刚度的频率折减系数敏感区段的范围无明显影响，仅影响频率折减系数的值。

(4) 考虑剪切变形后，剪力键刚度无穷小时(子梁间无连接状态)，连续组合梁的各阶频率折减系数不再趋近于相同值，其各界频率趋近值均大于不考虑剪切变形的情况，且阶数越高趋近值越大。

(5) 全长为L的n跨连续钢-混组合梁基频分析时，若忽略剪切变形的影响且控制误差在5%以内，则需L/(nh)>10。

附录A

对于两跨连续组合梁，式(20)变为

(A.1)

式中，R1为中间支座的未知反力。由φ(x1)=0，可得

(A.2)

如前所述，2×L的等跨径连续组合梁，其第(2k-1)阶自振频率与跨径为L的简支组合梁的第k阶自振频率相等。因此其第(2k-1)阶自振频率由式(18a)求解；其他阶频率由式(A.2)求解。式(A.2)中，支座反力R1不为0，所以中括号中的式子必须等于0，式(A.2)才成立。使用MATLAB软件及前述步骤1～步骤5，即可求得组合梁的自振频率。需要说明的是，此时步骤1～步骤5中的detN=0变为式(A.2)的中括号中的式子等于0。