水平激励下带竖向隔板的二维矩形储箱中流体晃动研究

温国正， 王佳栋， 曹占雪， 赵士琳

(江苏大学 土木工程与力学学院，江苏 镇江 212013)

部分充液的储液系统在受到外部扰动时能够观察到自由液面出现波动。而流体的晃动可能会导致储液系统发生严重的问题，产生巨大的安全隐患。为了控制储液系统中流体的晃动，可以在储液系统中增加额外的子结构。例如，水平隔板和竖向隔板[1]。流体晃动产生的问题涉及各种实际应用与工程问题。比如，由于地震引起的流体剧烈晃动导致的储油罐发生火灾[2]。化工原料的储存、航天飞机的储油箱以及浮式生产、储存、装卸平台等[3]。所以对于储液系统流体的晃动控制研究具有重要的工程意义。

Cho[4]使用格林函数匹配本征函数展开法(matched eigenfunction expansion method,MEEM)研究了底部带孔的弹性隔板的二维矩形储箱中隔板参数对流体晃动的影响。王佳栋等[5]研究了带环形隔板的部分充液的刚性圆柱罐中流体的微幅晃动特性。房忠洁等[6]使用半解析方法研究了带水平隔板的二维矩形渡槽中隔板参数对固有频率的影响。应磊等[7]使用流体子域法研究了带刚性隔板的矩形储箱在水平与俯仰激励下的晃动响应。Wang等[8]研究了带多个刚性隔板的圆柱形储液罐在水平激励下自由液面的波高、液动压力以及力矩。Jin等[9]通过试验的方式研究了矩形储箱中安装水平带孔隔板对晃动的抑制效果。Wen等[10]使用线性波理论和达西定律求解了瞬态和稳态运动的补充解，并且以结构动力学的角度建立了考虑多孔介质引起的晃动阻尼的等效力学模型。Koh等[11]对CPM(consistent particle method)进行了优化，弱化了控制方程中位置的影响，通过与试验对比验证了其方法，然后研究了三维矩形储箱的晃动特性。Meng等[12]研究了安装在矩形储箱底部的竖向隔板对流体晃动的抑制作用。

很多学者研究了竖向隔板对矩形储箱中流体晃动的抑制作用，但是大部分是针对安装在储箱底部的竖向隔板。为了进一步优化隔板的安装位置，本文建立了隔板在自由液面处的解析模型，同时使用了Meng等的方法建立了隔板在储箱底部的解析模型。然后对这两种隔板对流体的晃动控制进行了比较研究，结果表明安装在自由液面处的隔板具备更加显著的流体晃动控制能力。

1 物理模型

图1 储箱隔板安装示意图Fig.1 Schematic diagram of container baffle installation

图2 水平激励下带竖向隔板的二维矩形储箱Fig.2 Rectangular container with vertical baffle under horizontal excitation

本文将采用流体子域法求解图2所示的晃动频率与模态，设图2(a)中的流体的速度势函数为φ(x,z,t)，由于储箱中流体为理想流体，因此φ(x,z,t)满足拉普拉斯方程

(1)

流体速度在x和z两个方向上的分量满足如下条件

(2)

储箱中流体做线性微幅晃动，速度势函数满足自由液面条件

(3)

(4)

速度势函数在相邻的子域间的界面上Γk(k=1,2,3)满足速度和压力连续条件

(5)

式中:n为相邻子域间的界面Γk(k=1,2,3)上的法向单位矢量；p,q为相邻的子域。

2 自由晃动频率与模态

首先假设储箱处于静止状态，储箱中流体做自由晃动。如图2(a)所示，各个流体子域的速度势函数在储箱壁面上满足如下边界条件

(6)

在储箱底面上满足如下边界条件

(7)

在隔板上满足如下边界条件

(8)

流体在做微幅晃动时，流体的摄动速度势函数可以设为如下形式

φ(x,z,t)=jωejωtΦ(x,z)

(9)

(10)

将式(9)分别代入式(6)、式(7)和式(8)，通过使用分离变量法即可求得每个流体子域所对应速度势函数的形式解

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

将式(13)和式(14)代入自由液面条件式(3)可得

(21)

(22)

将式(15)～式(22)通过加权积分消去方程中的空间坐标，截断展开项即可得到关于待定系数的线性方程组

([D]-Λ2[K]){A}=0

(23)

(24)

式中，N为式(15)～式(22)中无穷级数的截断项数。通过式(23)可以求出矩形储箱的固有频率。为验证本文方法的正确性，将隔板在自由液面处的解与ADINA(automatic dynamic incremental nonlinear analysis)进行比较研究，隔板位置取为xb=0.5 m，考虑三个不同的隔板高度h=0.7 m,0.8 m,0.9 m。表1给出了本文方法与ADINA解的前10阶的固有频率的比较。如表1所示，本文方法的结果与ADINA的结果基本吻合。

表1 本文方法解与有限元解的比较Tab.1 Comparison study of Λ for present and ADINA’s solution

3 水平激励下的初始条件和边界条件

因为储箱壁面与隔板均为刚性，所以流体不能渗透和脱离，当储箱在水平方向上受到水平激励s(t)时，流体速度势函数在左右两侧壁面上应满足如下边界条件

(25)

在隔板上应满足如下边界条件

(26)

在储箱底面应满足如下边界条件

(27)

流体运动的初始条件如下

(28)

在此考虑自由液面的波动，根据线性晃动理论，可得

(29)

式中，f为自由液面波高。速度势函数φ可以分解为两部分：流体的刚体速度势φA(x,z,t)和摄动速度势φB(x,z,t)，即

φ=φA(x,z,t)+φB(x,z,t)

(30)

根据式(1),φA(x,z,t)和φB(x,z,t)分别满足拉普拉斯方程

∇2φA(x,z,t)=0，
∇2φB(x,z,t)=0

(31)

将φA(x,z,t)和φB(x,z,t)分别代入式(25)～式(31)得

(32)

(33)

(34)

(35)

(36)

(37)

(38)

根据φA所满足的控制方程和边界条件，设流体的刚体速度势为如下形式

(39)

将式(38)和式(39)代入式(37)可得

(40)

(41)

4 动力响应方程

将式(38)和式(41)代入式(40)可得

(42)

(43)

(44)

(45)

使用多哈梅积分对式(43)进行求解，可得其一般形式的解

(46)

(47)

将式(47)代入式(29)可得储箱中流体的自由液面波高

(48)

根据伯努利方程可得流体晃动液动压力

将作用在储箱侧壁与隔板上的液动压力进行积分可得储箱的基底剪力。对于如图2(a)所示的隔板在自由液面处的情况，其基底剪力如下

(50)

液动压力在储箱壁面、隔板以及底面上产生的力矩为

(51)

(52)

(53)

式中，Sbottom为储箱底面与流体的接触表面。

将式(51)～式(53)相加即可得倾覆力矩

M=Mwall+Mbaffle+Mbottom

(54)

5 比较研究

为了验证本文方法的准确性，将本文方法解与有限元软件ADINA的仿真结果进行比较研究。模型参数取为H=1 m,b=1 m,xb=0.5 m,h=0.5 m, 在储箱上施加如下激励

(55)

式(55)中，所选激励频率为储箱无隔板时的第1阶流体晃动频率。本文针对两种方法得到的自由液面波高的时程曲线进行了比较研究。图3和图4分别给出了隔板在自由液面处和隔板在储箱底部的比较结果。显而易见，二者具有较高的一致性。从而验证了本文方法的准确性。

图3 隔板在自由液面时波高时程曲线Fig.3 The time history of the wave height when the baffle is at free surface

图4 隔板在底部时液面波高时程曲线Fig.4 The time history of the wave height when the baffle is at bottom

6 稳态响应

s(x)=X0sin(ωxt)

(56)

(57)

6.1 自由液面波高

将式(57)代入式(48)可得自由液面波高的稳态解。图5和图6给出了自由液面波高幅值随隔板高度的变化规律，在此考虑了三个不同的隔板位置。

图5 隔板在自由液面，波高随隔板高度的变化图Fig.5 The wave height varies with the height of baffle when the baffle is at free surface

图6 隔板在底部，波高随隔板高度的变化图Fig.6 The wave height varies with the height of baffle when the baffle is at bottom

从图5可以看出，隔板安装在自由液面时，随着隔板高度的增加，fmax迅速减小到零点。经过零点之后，fmax随着隔板高度的增加缓慢增加。对应于三个不同的隔板位置，隔板高度分别取h=0.655 m,h=0.29 m,h=0.2 m时，波高幅值为零。

从图6可以看出，隔板安装在底部的矩形储箱的fmax随着h的增大单调递减。对应于三个不同的隔板位置，能够达到的最小值为0.073 m，0.045 m，0.043 m。

图7和图8给出了自由液面波高幅值随隔板位置的变化曲线，在此考虑了三个不同的隔板高度。

图7 隔板在自由液面，波高随隔板位置的变化图Fig.7 The wave height varies with the position of baffle when the baffle is at free surface

图8 隔板在底部，波高随隔板位置的变化图Fig.8 The wave height varies with the position of baffle when the baffle is at bottom

从图7可以看出，隔板安装在自由液面时，随着xb的增加，fmax逐渐减小到最小值，对于h=0.3 m，h=0.7 m的fmax的曲线会到达零点。之后，fmax随着xb的增加逐渐增加。对于两个不同隔板高度h=0.3 m，h=0.7 m时，隔板距离左侧壁面的距离为xb=0.295 m，xb=0.48 m时，波高幅值为零。

从图8可以看出，隔板安装在底部的矩形储箱的fmax随着xb的增大逐渐减小到最小值后逐渐增大。

通过对比图5～图8可以发现，在h和xb都一样的情况下，安装在自由液面处的隔板对自由液面波高的抑制效果要远远优于安装在储箱底部的隔板。

6.2 基底剪力

将式(57)代入式(50)可得基底剪力的稳态解。图9和图10给出了基底剪力随隔板高度的变化规律，在此考虑了三个不同的隔板位置。

图9 隔板在自由液面，基底剪力随隔板高度的变化图Fig.9 The hydrodynamic force varies with the height of baffle when the baffle is at free surface

图10 隔板在底部，基底剪力随隔板高度的变化图Fig.10 The hydrodynamic force varies the height of baffle when the baffle is at the bottom

从图9可以看出，隔板在自由液面时，Fmax随着隔板高度的增加呈现出先减小后增大的非单调变化趋势，对应三个不同位置的隔板，隔板高度分别取h=0.14 m，h=0.125 m，h=0.14 m时，基底剪力幅值到达最小值。除此之外，当隔板高度大于0.4 m时，基底剪力幅值的变化趋于平缓，隔板高度的继续增加对其影响不大。xb=0.3 m和xb=0.7 m对应的曲线完全重合，这主要是因为这两个位置关于储箱的中轴线(x=0.5 m)对称，与之对应的晃动频率是相等的，相应的晃动模态也是关于中轴线是对称的。

从图10可以看出:当xb=0.5 m和xb=0.7 m时，Fmax随着h的增大单调递减；当xb=0.3 m时，Fmax先随h的增大缓慢增加至最大值，然后再逐渐减小。隔板安装在底部时，高度较小的隔板对晃动的抑制效果不明显，此时刚体速度势是影响基底剪力的主要因素，这就造成了xb=0.3 m和xb=0.7 m对应的曲线在开始时有较大的差异。隔板的抑制效果随着高度的增加而增加，xb=0.3 m和xb=0.7 m对应的曲线的差异也随之减小，当隔板高度大于0.63 m时，两条曲线基本吻合。

图11和图12给出了基底剪力随隔板距离左侧壁面距离的变化规律，在此考虑了三个不同的隔板高度。

从图11可以看出，隔板安装在自由液面时，随着xb的增加，Fmax逐渐减小到最小值后逐渐增大。且曲线关于x=0.5 m基本对称。这是因为隔板安装在自由液面处，其晃动抑制的效果非常显著，此时摄动速度势是影响基底剪力的主要因素。从图12中可以看出，隔板安装在储箱底部时，Fmax先随着xb的增大逐渐减小到最小值，然后再随之增大。

通过对图9～图12的分析可得，隔板安装在自由液面比隔板安装在底部对基地剪力的抑制效果更显著。

6.3 倾覆力矩

将式(57)代入(54)可得倾覆力矩的稳态解。图13和图14给出了倾覆力矩随隔板高度的变化规律，在此考虑了三个不同的隔板位置。

图13 隔板在自由液面，倾覆力矩随隔板高度的变化图Fig.13 The hydrodynamic moment varies with the height of baffle when the baffle is at free surface

图14 隔板在底部，倾覆力矩随隔板高度的变化图Fig.14 The hydrodynamic moment varies with the height of baffle when the baffle is at bottom

从图13可以看出，隔板在自由液面时，Mmax随着h的增大呈现出先减小后增大的趋势。对应于三个不同的隔板位置，隔板高度分别为h=0.12 m，h=0.105 m，h=0.12 m时，倾覆力矩幅值达到最小值。除此之外，当隔板高度大于0.4 m时，倾覆力矩幅值的变化趋于平缓，隔板高度的继续增加对其影响不大。xb=0.3 m和xb=0.7 m对应的曲线完全重合，图9中对应的基底剪力曲线也是重合的，其原因是一致的，说明安装在自由液面处的竖向隔板对基底剪力和倾覆力矩同时具备较为显著的抑制能力。

从图14可以看出，Mmax随着h的增大缓慢减小到最小值后出现短暂的缓慢增加。对应于xb=0.3 m和xb=0.7 m的曲线之间的差异随着隔板高度的增加而减小，当隔板高度大于等于0.5 m后，两条曲线基本吻合，这说明隔板对倾覆力矩的影响主要取决于其高度。

图15和图16给出了倾覆力矩随隔板高度的变化规律，在此考虑了三个不同的隔板位置。从图15可以看出隔板安装在自由液面时，随着xb的增加，Mmax逐渐减小到最小值后逐渐增大。且曲线关于x=0.5 m呈现一定的对称性。这是因为隔板安装在自由液面处，其晃动抑制的效果非常显著，此时摄动速度势对倾覆力矩起主导作用。从图16可以看出，Mmax都随着xb的增大逐渐减小到最小值后逐渐增大。

图15 隔板在自由液面，倾覆力矩幅值随隔板高度的变化图Fig.15 The hydrodynamic moment varies with the position of baffle when the baffle is at the free surface

图16 隔板在底部，倾覆力矩幅值随隔板位置的变化图Fig.16 The hydrodynamic moment varies with the position of baffle when the baffle is at bottom

综合分析图13～图16可以得到，隔板安装在自由液面比隔板安装在底部对倾覆力矩幅值的抑制效果更显著。

6.4 不同流体深度下隔板高度对晃动响应的影响

为了研究在不同液体深度下竖向隔板的高度对晃动响应的影响，在此考虑三个不同的液体深度：H=0.6 m,H=0.8 m,H=1 m。当液体深度取H=0.6 m时，隔板高度h不能超过0.6 m，为了便于分析，对于不同的液体深度，隔板高度h的取值范围统一为：0.1 m≤h≤0.5 m。隔板水平位置固定在xb=0.5 m处。图17～图19分别给出了自由液面波高、基底剪力和倾覆力矩随着隔板高度的变化趋势。

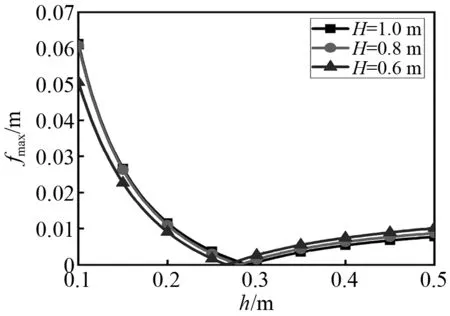
图17 隔板在自由液面，不同流体深度下，自由液面波高随隔板高度变化图Fig.17 The wave height varies with the height of baffle when the baffle is at free surface and the liquid depth is 0.8 m

图18 隔板在自由液面，不同流体深度下，基底剪力随隔板高度变化图Fig.18 The hydrodynamic force varies with the height of baffle when the baffle is at free surface and the liquid depth is 0.8 m

图19 隔板在自由液面，不同流体深度下，倾覆力矩随隔板高度变化图Fig.19 The hydrodynamic moment varies with the height of baffle when the baffle is at free surface and the liquid depth is 0.6 m

如图17所示，为矩形储箱内液体深度分别为1 m，0.8 m和0.6 m时的自由液面波高的变化趋势图。显而易见在不同流体深度下自由液面波高随着隔板高度的变化趋势是相同的。并且，在相同的外部激励作用下，在波高幅值达到最小值之前，自由液面波高随着流体深度的降低而降低；在波高幅值达到最小值之后，则与之前相反。

如图18所示，不同流体深度下基底剪力的变化趋势是相同的，随着隔板高度的增大，基底剪力先迅速降低到最小值，然后呈现缓慢增大的趋势。

如图19所示，在液深为H=1 m,0.8 m时，倾覆力矩先随着隔板高度的增大迅速下降到最小值，然后呈现缓慢的上升。在液深为H=0.6 m时，倾覆力矩随着隔板高度的增大而缓慢增大。

7 结 论

本文通过半解析的方法研究了带垂直隔板的二维矩形储箱在水平激励下的晃动响应。研究了垂直隔板的安装位置、隔板的高度和隔板就离左侧壁面的距离与自由液面波高、基底剪力和倾覆力矩的关系。得到了如下的结果：

(1)隔板安装在自由液面时，隔板对自由液面波高、基底剪力、倾覆力矩同时具备较为显著的抑制能力，并且可以通过调整隔板的高度和位置可以使自由液面波高幅值为零。

(2)隔板安装在底部时，隔板必须具备一定的高度(h>0.5 m)才能对流体晃动产生一定的影响。

(3)通过比较分析，当隔板高度(h)和隔板位置(xb)完全相同的情况下，安装在自由液面处隔板对流体晃动控制效果要远好于安装在储箱底部的隔板。

附录A