例谈“空间角”的求解策略

张 宇

江苏省常熟市浒浦高级中学

“空间角”是近年高考中的高频考点，求解空间角的常用方法就是“空间向量法”，此外，还可以利用几何法求解空间角.此类问题侧重考查学生的空间想象能力、化归能力以及运算能力.

1类型一:求解异面直线所成的角

解决异面直线成角问题，可利用空间向量方法，也可利用几何法——先画出图形，通过作平行线，将异面直线所成角放置在某个三角形中，再借助余弦定理加以求解.

例1已知直三棱柱ABC-A1B1C1的所有棱长都相等，M是A1C1的中点，N是BB1的中点，求异面直线AM与NC1所成角的余弦值.

图1

解法1：空间向量法.

图2

解法2：几何法.

把直三棱柱补形为直四棱柱(各条棱长相等)，如图2.设直三棱柱的棱长为4，取B1E=1，连接EN，故EN∥AM,所以∠ENC1为异面直线AM与NC1所成角.

于是，在△ENC1中，由余弦定理得

2类型二：求解直线与平面所成的角

解决线面成角问题，可利用空间向量方法，也可利用几何法——适当作辅助线，利用线面角的概念，先将线面角放置在某个直角三角形中，再通过求解直角三角形即可获解.

(Ⅰ)求证：直线AB⊥平面DEF；

(Ⅱ)求直线BE与平面DAB所成角的正弦值．

解析：(Ⅰ)略.

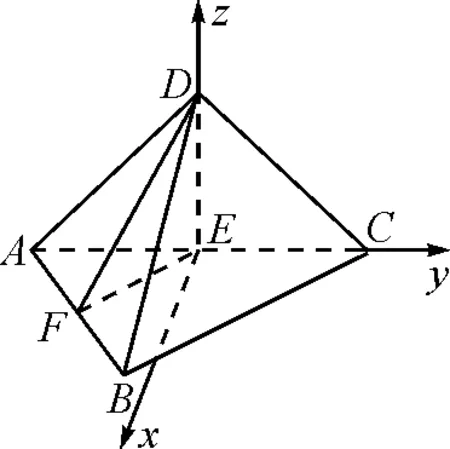
图4

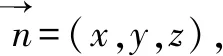
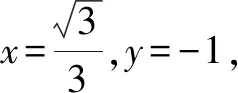
方法2：几何法.作EO⊥DF，垂足为O，连接OB.由(Ⅰ)可知AB⊥平面DEF，又EO⊂平面DEF，则AB⊥EO.又DF∩AB=F，所以EO⊥平面DAB，从而直线BE在平面DAB内的射影为OB，因此∠OBE就是直线BE在平面DAB所成的角.

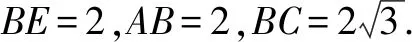
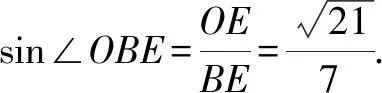
评注：处理立体几何中有关“翻折”问题的关键是抓住“翻折”前后两个图形的特征关系，往往需要先理清哪些量发生了变化，哪些量没有发生变化；然后再灵活运用空间向量法或几何法，化繁为简，可有效降低试题难度.

3 类型三:求解两个平面所成的角

解决面面所成角问题，可利用空间向量方法加以求解，也可利用几何法——适当作辅助线以及推理论证，先得到二面角的平面角，再将该平面角放置在某个三角形中，通过解三角形求解.

图5

(Ⅰ)求证：直线BE∥平面PDF；

(Ⅱ)求二面角P-DF-C的余弦值.

解析：(Ⅰ)略.

图7

(Ⅱ)方法1：空间向量法.

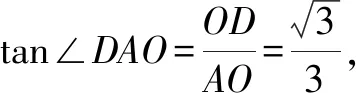
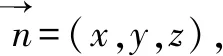
方法2：几何法.

因为BD⊥PC，AC是PC在平面ABCD内的射影，所以BD⊥AC，则四边形ABCD是菱形.

又由F是AB的中点，可知DF⊥AB.因为PA⊥平面ABCD，所以PA⊥DF.又PA∩AB=A，所以DF⊥平面PAB，于是DF⊥BF,DF⊥PF.故∠PFB就是二面角P-DF-C的平面角.

通过以上归类解析可知，处理“空间角”问题时，若选用“空间向量法”，则关键在于恰当建系、准确计算直线方向向量的坐标或平面法向量的坐标，其优点是思路简单、明了，缺点是运算量较大.若选用“几何法”，则关键在于借助图形、将空间角问题等价转化为平面角问题，其优点是计算较少，缺点是往往需要巧作辅助线，思维量较大.Z