利用均值不等式求函数最值的六种方法
2023-02-11 03:35洪家凤
中学数学杂志 2023年1期
曹 昕 洪家凤
安徽省涡阳县第二中学 安徽省涡阳县第四中学
均值不等式是高中数学的一个重要公式,常出现在填空、选择题中,结合不等式的性质进行考查,部分大题解答过程中也常用到.下面结合实例给出求函数最值的6种方法.
1 整体代换法
在利用均值不等式求最值时常会遇到一些较复杂的运算,直接运算可能比较复杂甚至无法得出结果,而采用整体代换的方法.有时可以简化运算.







2 取平方法


解:由2x-1和5-2x的和为定值,得

≤4+(2x-1)(5-2x)=8.

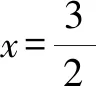
3 变量变换法

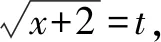

当t=0时,y=0.

4 凑系数法
凑系数是使用配凑法解题的一个重要思路,常用在形如y=x(a-bx)(a,b为常数)的函数求最值,只需要将x(a-bx)配凑成和为定值的式子,即在x前面配上一个系数b使bx+(a-bx)=a,从而使等式满足求最值的条件进而解决问题.
例4当0 分析:在利用均值不等式求最值时,目标等式中需要满足和或者积为一个定值.本题由已知条件0 解:y=x(8-2x) 当且仅当2x=8-2x时,上式等号成立. 即当x=2时,y=x(8-2x)的最大值为8. 解:因为x =-2+3=1, 所以当x=1时,函数f(x)的最大值为1. 所以,所求函数值域为(-∞,1]∪[9,+∞). 总而言之,利用均值不等式求解最值问题时,要熟练掌握变形技巧,积极地为利用均值不等式求解创造条件;要善于总结归纳解题方法,多加练习提高解题能力,提升利用均值不等式求最值问题的解题技巧.5 凑项法
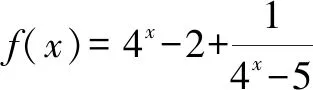



6 分离法


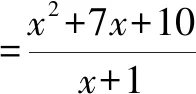
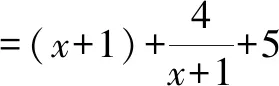
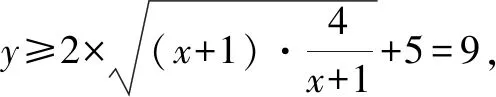

猜你喜欢
中学生数理化(高中版.高二数学)(2022年3期)2022-04-26
中学生数理化(高中版.高二数学)(2022年1期)2022-04-26
新世纪智能(教师)(2021年2期)2021-11-05
中学生数理化(高中版.高考数学)(2021年12期)2021-03-08
河北理科教学研究(2020年3期)2021-01-04
中学生数理化(高中版.高二数学)(2020年11期)2020-12-15
数学小灵通(1-2年级)(2020年9期)2020-10-27
新高考·高一数学(2018年5期)2018-11-22
电子制作(2018年10期)2018-08-04
电子制作(2018年12期)2018-08-01

