具有下界约束混料试验的Monte-Carlo渐近最优设计

杨晓珍

（凯里学院理学院 贵州凯里 556011）

自20世纪二十年代初，由Fisher.R.A等人提出试验设计的统计方法，许多统计学家根据不同的情况提出了各种试验设计方案，例如，正交试验设计，均匀试验设计，回归混料试验设计等[1-2]。这些重要的设计方法已在社会生产和实践中得到了广泛的应用和推广。

近年来，最优试验设计逐渐发展，称为一门新学科，基于最优试验设计所产生的数据不仅能够便于统计推断，而且还能简化计算，提高效率。最优试验设计的应用非常广泛，遍及工农业的生产和科学实验的各项领域[3-4]。其中D-准则和MV-准则是评价最优设计的常用准则，关于D-准则下的最优设计也有很多的推广。然而，对于含有较多未知变量的试验设计，由于难以求得其信息矩阵的行列式或逆矩阵的显式表达，所以难以得到各类最优准则下的精确最优设计解。为此，许多学者提出了不同的算法，Fedorov最先提出了D-最优设计的算法[5]，Evans提出了Dn-最优设计的直接扩张法[6]，1974年，Mitchell给出了D-最优设计的DETMAX算法[7]，通过增加或删除设计点的方式使得信息矩阵行列式达到最大，直到它满足试验的精度要求.后来，Galil和Kiefer对该算法进行了优化[8]，进一步节省了算法空间和时间。这一算法能有效获得设计域内的D-最优准则下的设计点，并且误差可控。对于其他一些准则，例如MV-准则，G-准则，Ds-准则，E-准则[9]等等，关于MV-准则下的有效算法的文献不多，而不同的准则下所涉及到的算法也不同，在使用的过程中需要区别使用。

许多文献都尝试构造随机搜索算法来得到最优设计[10-14]，本文在此基础上，尝试在D-准则和MV-准则下，使用相同的方法——Monte-Carlo方法，通过大量随机数模拟的方式，求出不同准则下的近似最优解，并且通过验证，说明模拟效果良好。

一、具有下界约束的混料模型

混料是指若干种不同成分的物质混合或合成一种稳定的物质或产品。这些产品的每种成分的多少是用相对量表示的，这种相对量就是所用成分在总量中所占比例。很多情形下，我们所需要考虑的是完全混料模型，即各成分所占比例都要大于零。有甚者，通过实践经验可以首先规定各中成分所占比例的下界，这一类模型称之为具有下界约束混料模型。

对于q分量有下界约束的混料系统，响应是各分量比例x1,x2,…,xq的函数，各个分量的约束下界分别为a1,a2,…,aq，由各分量比例所确定的q-1维单纯形[15]可表示为:

η(xj,Θ) 是含有未知参数且形式已知的函数，Θ=(θ1,θ2,…,θm)T是未知待估的参数向量，ε=(ε1,ε2，…,εN)T为随机误差向量，并且假设E(εj)=0，Var(εj)=σ2，j=1,2,…,N，且Cov(εi,εj)=0(i≠j)。一般还假设随机误差向量服从正态分布，即有ε～N(0 ,σ2IN)，其中IN为N阶单位阵。

记Y=(y1,y2,…,yN)T为试验结果，(x1,x2,…,xN)∈X为给定的试验条件，X为拓扑空间上的紧集，称之为设计域。我们将N次试验的试验点记作，其中共有k个不同的设计点，记为x1,x2,…,xk.假设在试验点xi处进行了ri次试验，记wi=ri/N为试验点xi的权系数。

称ξ∈为一个具有测度的k点设计，称为设计空间.如果函数η(x,Θ )是关于参数与各分量函数的一个线性组合，即可以表示为：

当det(M(ξ))≠0时，称ξ为一个非奇异的设计。一般考虑的设计都假定为非奇异的。在试验设计中，很多准则都是由关于信息矩阵的判定函数来衡量的。记在准则φ下的判定函数为Φφ(M(ξ))。

D-准则[1]的原理是将信息矩阵的行列式最大化，从而使得参数向量Θ的置信椭球体积最小。D-准则可表述为：

在D-准则下，关于信息矩阵的判定函数为:

若模型(2)可以表示为参数向量线性组合的形式，即:

以Mij表示M-1(ξ)中第i行j列的元素，则有

在MV-准则下，关于信息矩阵的判定函数为:

信息矩阵在最优设计中扮演这重要的角色。当变量较多时，信息矩阵的行列式或是逆矩阵难以求得显式结果，所以要解得精确的最优设计是比较困难的。以下先使用Monte-Carlo方法来构造随机试验点样本，然后在随机样本中求取信息矩阵的行列式的近似极大值，并找到相对应的试验点。

二、Monte-Carlo方法构造试验点样本

对于(1)所示的q-1维单纯形Sq-1，若Sq-1不是一点或是空集，则称混料问题是非退化的有下界约束问题。构成非退化的混料问题的充要条件是：

且各分量还应具有隐上界约束：

设A是非退化的有下界约束的混料单纯形中的任意一点，我们可以通过线性变换的方式将Sq-1中的自然分量坐标转换为无约束的混料单纯形中的坐标。记点A的自然分量坐标及拟分量坐标分别为：

令Ιq为q阶单位阵，a=(a1,a2,…,aq)T为约束下界值构成的向量，再记1表示元素全为1的q维向量。

则两种坐标间的变换关系为：

若D-1存在，(6)式的逆变换为：

这样，经过线性变换后拟分量的全集就构成一个无约束的混料单纯形，记作：

MC1步:生成n组无约束的随机混料试验点。

由U[0,1]生成n个随机数，记作Z=(z,z,…,z)T。

111121n由于总体Z为连续型随机变量，为了尽可能的使抽取的随机数互不相同，我们可以将抽取随机数的精度提高，例如要求抽取的随机数保留小数点后6位，这样以来能使得抽到相同的随机数的概率变得很小。再令

Z1,Z2,…,Zq-1都是随机向量，且满足j=2,3,…,q-1；Zq是由前q-1个随机向量所确定的常值向量。

矩阵Z=(Z1,Z2,…,Zq)是一个n×q阶矩阵。容易验证Z各行元素和为1，记矩阵Z的第k行为：

这里，τk中各个元素间并不独立，对于任意的zjk(j=2,3,…,q-1)都是由前j-1个元素所共同确定的。τk中各元素的联合密度函数可以表示为：

其中I{⋅}为示性函数。

又因为Z1中各元素相互独立，由此可知Z2,Z3,…,Zq-1中各个元素也相互独立。则各τk，k=1,2,…,n是相互独立的，即有。

当n→∞时，τ1,τ2,…,τn能均匀地充斥在整个单纯形内部。记

是τk为中心δ为半径的邻域，对于任意的δ＞0，应有

MC2步：由(7)将无约束的随机混料试验点转换为具有下界约束的拟分量坐标。

例如，三分量和四分量混料系统取下界约束值分别取a=(0.1,0.2,0.1)T，a=(0.3,0.2,0.1,0.1)T，由MC1步生成500个无约束随机混料试验点，再转换为具有下界约束的拟分量坐标，使用文献[16]中的映射方法，得到如下图所示。

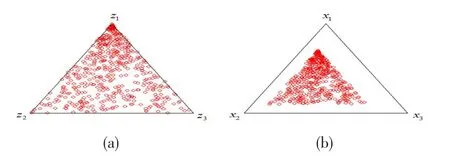
图1 无约束的随机混料试验点(a)(c)；转换后具有下界约束的拟分量坐标(b)(d)

MCS步:对于混料试验k点设计，在生成的随机点τ1,τ2,…,τn中随机抽取k点组成一个样本，重复抽取m次，记第j次抽取的样本为在τ(j)下的设计为：

将生成的各组随机数按组分别代入设计阵中，再计算信息阵为

表示第j个随机样本下的信息矩阵。

设若存在一个在测度(w1,w2,…,wk)最优设计ξ*，对于关于信息矩阵的某种最优准则Φ(M(ξ))，应有：

MCM步:在各M(ξj)(j=1,2,…,m)分别计算Φφ(M(ξj))值，按准则φ在ξ1,ξ2,…,ξm中选择出最优解，记作，将其作为全局最优解ξ*的个种近似解。

这里需要说明的是，如果在可行域上存在一个精确的最优解

由MCS步生成的随机点集为Ω={τ1,τ2,…,τn}，n＞k.F(Ω)表示由Ω生成的离散Borel域。下面分两种情况讨论。将简记为ξ*∈F(Ω)。

（1）如果ξ*∈F(Ω)，那么一次抽样恰好取到ξ*的概率为，m次抽样中能取到ξ*的概率为

理论上，可以由固定的α值确定需要抽样的次数m(α)，例如当m＞m(0.95)时，有α＞0.95，也就是我们总能找到一个确定的值m(α)使得取到最优设计点的概率充分的大。

（2）如果ξ*∉F(Ω)，进一步假设在准则φ下的判定函数Φφ(M(ξ))是关于变量(τ1,τ2,…,τk)的 连续函数，令是关于τ*的球形邻域，若对于任意的ε＞0，都存在一个常数δ(ε)＞0，使得当(τ1,τ2,…,τk)∈U(τ*,ε)时，有恒成立。则一次取样下的试验点组合τ=(τ1,τ2,…,τk)能落入U(τ*,ε)的概率为:

m次取样有试验点组合落入U(τ*,ε)的概率为α'=1-(1-p)m。所以当ε固定时，我们可以确定一个正整数m(ε)，使得当m＞m(ε)时，有成立。

虽然，不论是哪种情形，我们总可以得到这样一个结论：就是当m充分大的时候，能保证取到最优设计点或是随机试验点落入最优试验点的某个邻域的概率趋近于1，但是存在一个严重的问题，当随机点数n较大时，需要取的样本数量会大得惊人，而n如果较小，就不能保证随机试验点充分接近最优解。关于如何优化随机点数与抽样次数的问题仍有待进一步研究。以下我们讨论使用Monte-Carlo方法求出具有下界约束的三分量混料试验的近似最优解。

三、模拟近似最优设计

对于形如(3)中所示的回归模型的设计，按照Monte-Carlo方法构造随机试验点样本。经过转换后得到n个具有下界约束的随机混料试验点，令X为n×q阶矩阵，其中每一行对应了一个试验点的个分量坐标。然后将每一行元素代入设计阵，再由MCS步随机取出m个样本，计算出各组随机样本下的信息矩阵的行列式，并按升序排列为:

由于有随机数精度的要求，由各detM(ξ(j))(j=1,2,…,m)组成的样本中，一般不会出现打结的情形，如果该样本中存在结点，只需满足detM(ξ(m-1))＜detM(ξ(m))就可保证结点对结果不会造成影响，此时detM(ξ(n))的样本秩就等于n。再由detM(ξ(n))在原样本中的位置，例如detM(ξ(m))=detM(ξj)，那么就是对应的第j组随机试验点，使得样本信息矩阵的行列式在n次模拟中达到最大，从而可以将τ(j)视作最优设计点的一种近似.设若存在最优精确设计为ξ*，应有detM(ξ(m))→ detM(ξ*)，τ(j)→τ*(n→ ∞)成立。

下面我们通过一个实例来说明Monte-Carlo方法在求解渐近最优设计的有效性。

考虑三分量二阶Scheffé多项式回归模型

给定下界约束值向量为a=(0.1,0.2,0.1)T，在D-准则下，求解饱和设计的试验点。

按照2中所给出的步骤，首先生成1000组无约束的混料随机数，再将其转换为具有下界约束的随机数，由于设计的行列式值很小，为了便于比较，在计算行列式时将信息阵乘以100，即det(1 0 0M(ξj)).在MCS步随机抽取10000个随机试验点的样本，并重复MCM步若干次(由于随机取样不能完全取遍所有随机数的组合)，以确定在各种组合下的最优设计，经过计算可得到：

假设模型(11)参数真值为:

在模型中加入标准差为0.1的高斯噪声作为误差项，所得y值作为试验的结果，并假设在每个试验点重复三次试验，在所对应的试验点下列出对应的响应值，结果如表1所示:

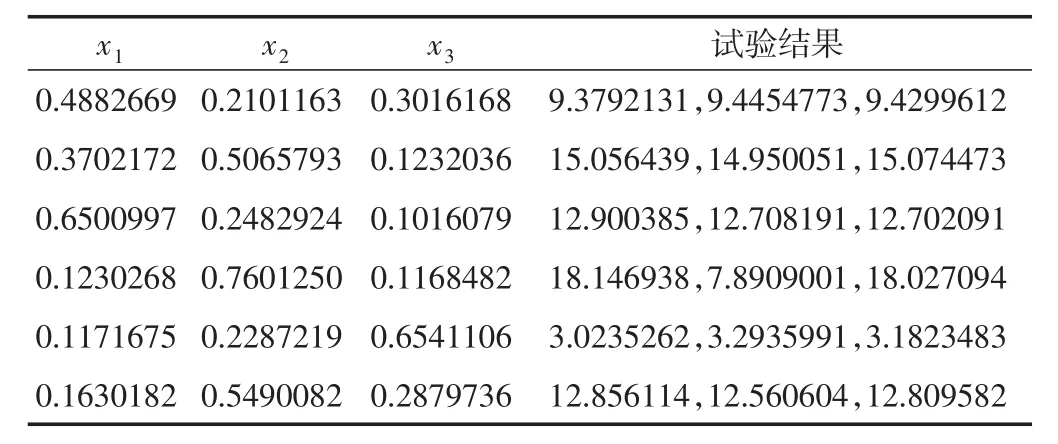
表1 饱和近似D最优设计

此时响应曲面及等高图如下图所示。

图2 饱和近似D最优设计的响应曲面与等高图

如果考虑带有测度的7点设计，假设含测度的设计为:

通过计算可得到参数的最小二乘估计为:

记表2和表3的设计分别为ξ6和ξ7，以上结果中，两种设计对一次项系数的估计值与真值偏离都不大，但交互项的系数估计值与真值之间都存在一定的偏离。导致这一结果的因素主要有两个:一是源于随机误差项的干扰：二是由于试验受约束条件限制，使得可行区域较小，所以得到的响应曲面的估计也是局部的。

表2 含测度的7点近似D最优设计

表3 饱和近似MV最优设计及试验结果

下面考虑在MV-准则下的近似最优解，此时关于信息矩阵的判定函数为:

与之前的讨论类似，由MC1步和MC2步生成具有下界约束的随机混料试验点，再有MCS步随机抽取其中的m个样本，计算出各组随机样本的信息矩阵及对应的逆矩阵，再计算出各组随机样本下的信息矩阵的逆矩阵的迹，记为：

并按升序排列为:

与D-渐近最优中的讨论类似，由各trj(j=1,2,…,m)组成的样本一般不会出现打结的情形，如果该样本中存在结点，只需满足tr(1)＜tr(2)，结点对结果就不会产生影响。此时tr(1)的样本秩就等于1，再由tr(1)在原样本中的位置，由tr(1)=trj=trM-1(ξj)确定对应的第j组随机样本，即使得。

此时，ξj下的设计点τ(j)可以作为MV-准则下最优设计点的一种近似，设若存在最优精确设计为ξ*，应有成立。我们仍考虑模型(11)，假设回归系数真值仍为(13)，生成1000个具有下界约束的混料随机数，然后重复取样10000次，重复MCM步若干次，计算出饱和设计下的的近似MV-最优解，并在模型中加入标准差为0.1的高斯噪声，由于信息矩阵中的元素较小，在循环过程中常会出现奇异设计，为避免这一情形，我们将设计矩阵乘以一个常数使之不易出现奇异情形，在此我们把信息矩阵乘以100再进行后续运算。

通过计算得到：

所得y值作为试验的结果.若在每个试验点重复三次试验，在所对应的试验点下列出对应的响应值，结果如表3所示:

图3 饱和近似MV最优设计的响应曲面与等高图

四、讨论

本文讨论了Monte-Carlo方法来求解D-准则和MV-准则下的近似最优解，并给出了实例模拟。虽然关于Scheffé多项式在各种最优性下的设计的文献已有很多，但对于含有约束条件的混料试验设计，在不同的准则下求解最优解的算法都是不同的，并且有的算法需要占用大量的内存。而Monte-Carlo方法原理相对简单，各种不同的最优准则可视作“选取条件”，在大量随机样本中抽取出符合这一条件的最优解，并且所得结果并不差，虽然这一结果并非精确解，但可以作为在该准则下最优解的一种参考。

使用Monte-Carlo方法求解最优准则下的精确解尚处于探索阶段，有很多问题还不能有效的解决。比如，随着分量的增加，需要生成的随机样本数就会呈指数次增长，只有这样才能保证近似解的有效性；此外，随机抽取混料试验点样本再进行比较的方法，效果不及全局搜索算法的结果，对于n个随机混料试验点，从中选取k点的设计，使用全局搜索需要运行的循环次数是，并且根据不同的信息阵需要编写不同的字典序程序，而Monte-Carlo方法则是在n个随机混料试验点中随机搜索，就像是“在茫茫数据中漫无目的地搜寻着最优点。”所以这种方法仍存在很大的局限性.关于以上问题都有待进一步研究。