具有群体性行为的捕食者-食饵系统稳定性分析

李梦婷，周 文

（安徽师范大学 数学与统计学院，安徽 芜湖 241002）

在自然生态系统中，大多数生物以群体形式活动，如鱼类[1]、浮游生物[2]等，这种现象引起了众多学者的关注。许多研究人员分析了具有群体性行为的捕食者-食饵系统[3-6]，并寻找合适的功能反应函数来描述这些群体性行为。Gause[7]指出食饵的群体性行为是一种防御模式，捕食者只能沿着食饵种群的边缘与之相互作用从而保护了内部的食饵群体，并提出了用平方根功能反应函数。Pal等[8]考虑了一种食饵具有群体性行为的捕食-食饵系统，用平方根模拟功能反应函数，分析了系统的局部稳定性和分支问题。平方根型功能反应函数的使用恰当地解释了相互作用是发生在种群边界上的现象。Liu等[9]研究了具有更加复杂的平方根型功能反应函数的捕食者-食饵系统：

其中，u表示t时刻食饵的密度，v表示t时刻捕食者的密度，β表示捕食者的死亡率，α表示食饵逃避攻击的能力，χϕ(v)v∇u表示捕食者向食饵移动的速度。

在生物数学中，具有时滞效应的生态系统稳定性和种群的空间分布是一项重要的研究课题。一般来说，在生物学系统中加入时滞会使模型更加符合实际，也会产生更加丰富的空间动力学行为[10-14]。Yan等[15]研究了如下的一类具有种群行为和Allee效应的捕食系统的复杂动力学：

其中，α,β,γ,d1,d2均是正常数，τ是时滞，表示食饵和捕食者的妊娠时间。

本文将通过理论和数值模拟来研究如下具有时滞和平方根功能反应函数的捕食者-食饵系统：

其中，u表示t时刻食饵的密度，v表示t时刻捕食者的密度，k0表示恐惧效应参数，m1表示捕食者的死亡率，m2表示捕食者的拥挤效应参数，b,ρ分别表示食饵逃避攻击的能力和转化率，d1,d2分别表示食饵和捕食者的扩散系数，τ是时滞，表示食饵的妊娠时间(x,t)∈Ω×R+，Ω ∈R2为边界光滑的有界区域，ν为∂Ω上单位外法向量。

系统（3）对应的常微分系统为

本文亮点工作有：将时滞与平方根功能反应函数相结合，探讨时滞对于系统平衡点稳定性的影响；与已有文献相比，Hopf分支曲线展示了转化率ρ与系统稳定区间的非线性关系现象为Hopf分支临界值）；通过数值模拟生动展示了时滞对于螺旋波斑图生成的影响。

1 平衡点的稳定性

为考虑模型具有的生物学意义，本文只研究系统（4）的正平衡点，令

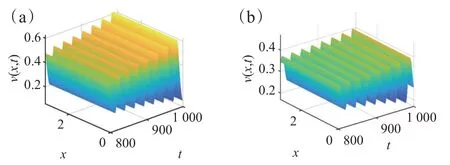
则系统（4）至少存在一个正平衡点E∗=(u∗,v∗)，满足v∗>0和0

图1 系统（4）在E∗=(u∗,v∗)处的等倾线图（k0=1.74,b=0.5,m1=0.2,m2=0.8）

接下来考虑系统（3）在正平衡点E∗处的稳定性，首先在(u∗,v∗)处引入小扰动：

系统（3）在正平衡点E∗=(u∗,v∗)处的线性化方程为

由以上分析可得，系统（3）的线性近似系统特征方程为

作出假设：H1:a11+ρa22<0；H2:a11a22-a12a21>0；H3:a11d2+ρa22d1<0。

定理2对任意波数k∈{0,1,2,…,}，当τ=0时，若H1-H3成立，则系统（3）的正平衡点E∗局部渐近稳定。

证当τ=0时，特征方程（8）变为

对任意k∈{0,1,2,…,}，由H1知M1>0，由H2,H3知M2+M3>0，由Routh-Hurwitz准则知E∗局部渐近稳定。

注记1由于ρ影响条件H1，H3是否成立，结合上述定理可知，若不考虑时滞，ρ影响正平衡点的稳定性。

2 Hopf分支分析

以时滞为Hopf分支的参数，利用线性稳定性理论对系统（3）进行稳定性和Hopf分支分析。设iω是方程（8）的纯虚根，则ω满足下列方程：

分离上述方程的实部和虚部，推出

将方程（11）两边平方再相加，得到

定理3对任意的τ>0，k∈{0,1,2,…,}，若满足条件H2-H5，则系统（3）的正平衡点E∗局部渐近稳定。

证设方程（13）有两个根Z1，Z2，由韦达定理，得到

综上，当条件H2-H5成立时，方程（13）有两个具有负实部的根，由Routh-Hurwitz准则可知定理成立。

注记2由于ρ影响条件H4是否成立，结合上述定理可知，若考虑时滞，ρ影响正平衡点的稳定性。

通过以上分析得到下列定理。

定理5若H1-H3,H6成立，则下述命题成立：（i）当τ∈时，系统（3）的平衡点E∗=(u∗,v∗)是局部渐近稳定的；（ii）当τ∈时，系统（3）的平衡点E∗=(u∗,v∗)是不稳定的。

通过以上稳定性分析和分支理论，得到如下ρ-τ关系（图2），其参数设置为k0=1.74,b=0.5,m1=0.2,m2=0.8,d1=0.02,d2=0.04。Hopf分支曲线将整个区域分成两个参数空间，即稳定区域和不稳定区域，可以看出转化率ρ与稳定区间呈正相关，且转化率越大稳定区间越大。

图2 系统（3）的Hopf分支

3 数值模拟

通过数值模拟直观展现出系统（3）在正平衡点E∗处的动力学行为，以此来验证理论推导的正确性。在本文所有数值模拟中，因为捕食者和食饵的空间斑图是类似的，所以这里仅研究食饵空间斑图的形成，部分参数设置为：k0=1.74,b=0.5,m1=0.2,m2=0.8,d1=0.02,d2=0.04。

3.1 平衡点的稳定性

当系统（3）的转化率ρ=0.8时，计算可知此时系统正平衡点E∗=(0.348 9,0.320 0)，Hopf分支临界值为=2.269 7。根据定理5 可知，若则系统正平衡点稳定；若则系统正平衡点不稳定。图3展示了时滞τ=1.9 和τ=2.32 时的食饵与捕食者的密度演化。图3（a）表示时滞为τ=1.9时的密度演化（蓝色为食饵密度演化，红色为捕食者密度演化），在t>500 后的密度值几乎不变，且数值均为平衡时的值，即u=0.348 9，v=0.320 0，这说明系统正平衡点是稳定的。图3（b）表示时滞为τ=2.32时的密度演化，随着时间的变化，捕食者与食饵的密度呈现振荡的变化趋势，系统正平衡点是不稳定的，这符合定理5的结果。因此，在足够长时间内捕食者与食饵的空间斑图都会朝着不规则的趋势变化。可以看出，在正平衡点稳定和不稳定的情况下捕食者和食饵的密度演化都基本相同。图4展示了时滞τ=1.9和τ=2.32时系统的相图。图4（a）表示时滞为τ=1.9 ∈时的相图，其呈现为一个点（0.348 9,0.320 0），即食饵和捕食者的密度值是一个固定值，其不随时间变化而改变，即该点为正平衡点E∗，这说明系统在正平衡点处呈稳定状态，也进一步说明了正平衡点是稳定的。图4（b）为时滞τ=2.32 ∈时的相图，为一个极限环，这表明在附近会产生Hopf分支现象，进一步证实了理论结果。

图3 系统（3）的捕食者与食饵的密度演化。（a）τ=1.9；（b）τ=2.32

图4 系统（3）的相图。（a）τ=1.9；（b）τ=2.32

3.2 Hopf分支

图5 τ=2.1，平衡点是稳定的

图6 τ=2.32，平衡点是不稳定的

3.3 二维空间斑图

参数设置同图3。图7和图8展示的是上述两种仅时滞τ取不同值情况下食饵的空间斑图演化过程，其中各子图右侧的颜色栏可作为食饵密度值的参照。图7表示的是时滞为τ=1.9 ∈情况，各子图分别展示了时间（a）t=0，（b）t=1500，（c）t=2 500，（d）t=4 500，（e）t=8 000和（f）t=10 000时刻下的空间密度分布。由于初始扰动，t=1500 时食饵的密度分布不均匀，但在t=2 500 时食饵的密度分布开始变得均匀，且一直到t=10 000时密度分布仍然均匀，且由数值结果发现长时间下食饵的密度一直在0.348 9 且与正平衡点u∗=0.348 9 相同，数值结果符合理论，证实了系统的正平衡点是稳定的；图8 展示的是时滞τ=2.32 ∈(+∞)的情况，各子图分别为（a）t=0，（b）t=1500，（c）t=2 000，（d）t=3000，（e）t=7 500和（f）t=10 000时刻下的空间密度分布，此时正平衡点是不稳定的。从图可知，规则的螺旋波随着时间的演化逐渐形成，而后螺旋波由边缘开始破碎，最后不规则的螺旋波斑图占据了整个区域。上述结果不仅证实了定理5的结论，而且揭示了时滞会对系统空间分布产生影响并使其出现螺旋波斑。

图7 τ=1.9时食饵的空间斑图

图8 τ=2.32时食饵的空间斑图

4 结论

时滞对捕食者-食饵系统的统动力学行为有重要的影响，本文分别从理论推导和数值模拟两方面研究了时滞对具有平方根型功能反应函数的捕食者-食饵系统的影响。结果表明：（1）无论有无时滞，转化率都会影响系统正平衡点的稳定性；（2）以时滞为分支参数时，转化率对Hopf分支的临界值有影响，并且在一定区间内，转化率的增大会导致临界值变大；（3）转化率不影响捕食者与食饵的密度，随着转化率的增加，其对时滞临界值的影响程度越来越小，在实际生物系统中可适当增大转化率来保持系统的稳定。