聚焦核心素养 优化例题设计

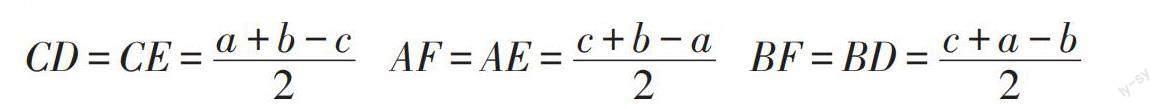
摘 要 核心素养是新义务教育课程改革的主旨理念，也是初中数学课堂教学的目标。例题是培育核心素养的重要途径，教师需要重视例题创新设计。通过“问题前置”，树立模型观念，构建数学模型；“拓展整合”，发散活跃思维，培养推理能力；“多变求同”，建立数形关系，培养几何直观能力；“自主创设”，形成思维网络，培养分析归纳能力等方法，将原生例题重新加工以达到不断优化例题教学，促进数学学科育人价值的实现。

关键词 初中数学 核心素养 例题教学 优化设计

作者简介：牟丽丽（1974— ），女，山东日照人，山东省日照市岚山区虎山镇初级中学高级教师，大学本科，研究方向：初中数学教学研究。

例题教学是数学课堂教学的重要组成部分，也是学生学习数学知识、培育核心素养的重要途径。初中数学例题具有基础性、探究性和典型性等特点，对培育学生核心素养具有非常重要的作用。一般来说，教材中的例題都是经过编者反复推敲后精心编选的，具有一定的代表性。但是在教学中面对的实际情况各不相同（如城乡差别、地域差别、学生认知水平差异等），教师需要根据实际情况，立足学生核心素养培养，对教材中的例题进行全方位剖析。通过更换、补充、拓展、整合或自主创设等方式，有针对性地对例题进行“二次设计”。在设计中重点突出针对学生的“建模”“推理”“几何直观”“综合分析”等能力的培养，以适应不同地区、不同学生的学习需求，从而优化例题教学[1]2-36。

下面以人教版九年级数学中习题设计为例，从培养和发展学生核心素养的角度，来阐述初中数学例题的优化设计策略。

一、“问题前置”，树立模型观念，构建数学模型

模型是数学学习中的一个重要概念，是例题设计不可或缺的关键要素。学生的数学学习过程，实际上是一个持续地建构模型和应用模型的过程。教师要重视学生已有经验，善于搭桥铺路，将问题前置，让学生体验从具象中抽象出数学问题、构建数学模型、得到结果、解决问题的过程。

例如，在“垂直于弦的直径”一节中，教材通过探究“圆是轴对称图形”得到“垂径定理”及其推论后，直接安排了一个实际应用的例题——求赵州桥主桥拱半径。

赵州桥（如图1所示）是我国隋代建造的石拱桥，距今约1400年的历史，是我国古代人民勤劳与智慧的结晶。它的主桥拱是圆弧形，它的跨度（弧所对的弦的长）为37 m，拱高（弧的中点到弦的距离）为7.23 m，求赵州桥主桥拱的半径（结果保留小数点后一位）。

根据题中描述的信息，学生能够在教师的指导下画出图形。但是通过图形直接构建模型，理解并掌握模型的思想方法，这对于理解能力与应用能力较弱的学生是非常困难的。所以，在对例题进行重新设计时，教师可以小梯度设置几个有梯度的问题，并将问题前置，让学生拾级而上，使其在层递式的观察、思考、讨论及体验中，逐渐掌握例题所呈现出来的数学思想与方法，建立相应的数学模型，并应用模型[2]。具体做法如下：

1.条件判别

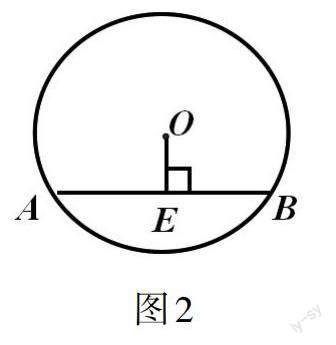
问题1：如图2所示，圆中一条弦AB，OE垂直于AB，垂足为点E，此图形中条件是否符合垂径定理的条件？若符合，可得出哪些结论？

问题1的设计是根据建构主义理论，启发学生调动已有学习知识和经验，使已有知识对新知识发生正向迁移。

2.建立模型

问题2：如图3所示，若半径R = 5，OE = 3，则AB = ____。

问题3：如图3所示，若AB = 8，OE = 3，则半径R = ____。

问题2和问题3的设计在于引导学生回顾勾股定理，使“垂径定理”与“直角三角形”等相关知识在意义上发生关联。引导学生以原有知识经验作为新知识的“生长点”，进行知识转换和处理，形成对问题的理解和解释，从而树立模型观念。

问题2和问题3解决后，学生就会发现：弦长、弦心距、半径三者关系恰好是直角三角形三边关系。学生初步建立起“垂径定理的应用转化为直角三角形求边长”的数学模型。

3.理解模型

模型建立后，需要进一步引导学生对模型所体现出的思想与方法深入理解。继续对原图形进行变形。

问题4：如图4所示，延长OE交圆于点F，若AB = 8，EF = 2，则半径R = ____。

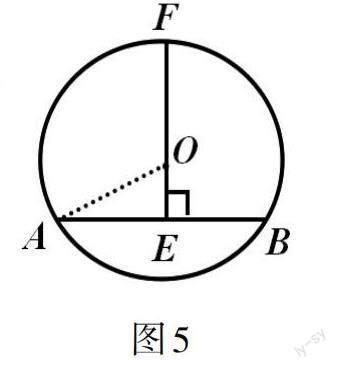
问题5：如图5所示，反向延长OE交圆于点F，若AB = 8，EF = 8，则半径R = ____。

问题4和5的设计意在拓展学生对垂径定理的变形应用，让学生直观感受垂径定理，并从本质上理解这一模型。

4.应用模型

此时呈现教材中的例题——“求赵州桥主拱桥的半径”。由于前面几个有梯度的问题铺设，学生很容易理解此模型的思想与方法。由“图形”得“模型”，赵州桥主拱求解问题也就很容易得到解决。

二、“拓展整合”，发散活跃思维，培养推理能力

教材中的例题均具有典型性，示范意义很强。但是教材中有些例题往往是一题一问，赋予学生的思维空间较小，不利于培养学生的思维深度和广度。《义务教育数学课程标准（2022年版）》强调要逐渐拓展和加深课程内容，适应学生的发展需求。因此在充分发挥例题示范功能的基础上，将例题加以引申、拓展是非常必要的。

例如，在“直线和圆的位置关系”一节中，内切圆的相关例题可以做如下设计。

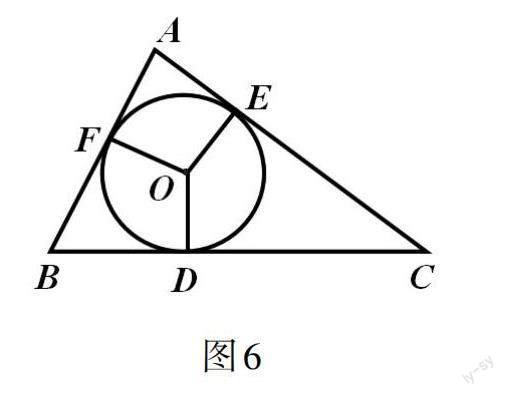
原题：如图6所示，△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F，且AB = 9 cm，BC = 14 cm，CA = 13 cm，求AF、BD、CE的长。

原题是在学习了切线性质、切线长定理及内切圆定义后给出的一道综合例题，例题融合了多个知识点，渗透了多种数学思想和方法，综合性强，关联度高，延伸性好，对拓展学生思维、提高学生分析问题、解决问题能力有很好的帮助[3]。

首先，引导学生探求解题思路。该题可以用方程思想设所求的这三条线段中一条长为x，根据题中的线段关系列方程求解；还可以设这三条线段的长分别为x、y、z，根据线段关系列方程组来解。

然后，让学生总结规律。若AB = c，BC = a，CA = b，继续求解上述三条线段的长。引导学生总结得到：

用字母来代替数值，其意义在于帮助学生在具象中抽象出数学问题，及时建立起一种“已知三角形三条边求切线长”的数学模型。

（一）拓展一：深化条件，探求新结论

学生在解决上述问题时，关注点往往在求切线长的方法上，思维太单一，而数学知识是相互联系的，这时教师可引导学生思考：由题设中的这些条件能否求解出其它的相关量？

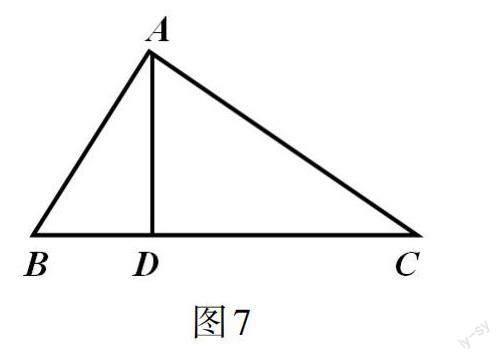
1.求面积。通过教师引导后学生就会发现，如图7所示，作BC边上的高，利用勾股定理关系AB2 - BD2 = AC2 - CD2，设BD = x或CD = x，列方程求出BD或CD，就可求得题设中三角形ABC的面积。代入数值，得出S△ABC = [1810]cm2。

基于此，学生可得出已知三角形三条边长，求三角形面积的结论，并掌握其求解方法。

2.求半径。由三角形面积公式，能够联想到底边与高的求解问题。教师可以进一步引导：如图8所示。已知三角形的面积为[1810]，能求出此三角形内切圆的半径吗？（即OF、OE、OD的长），思路是什么？

学生通过观察能够得出△ABC的面积为△AOB、△BOC、△AOC面积之和，于是得到[12（9+14+13）r=1810]，得r =[10]，进而得到三角形内切圆半径r、周长l、面积s的关系式[s=12lr]，将公式变形得到[r=2sl]。

通过深化条件，学生完成了内切圆半径与三角形边长、切线长以及面积等内在关系的探究，获得了新发现，形成了新结论，学生思维的触角得以向更深层次延伸和发展。

（二）拓展二：改变条件，化一般为特殊

教师改变题设条件，引导学生观察思考。如图9所示，把三条线段的长改为AC = 6 cm，BC = 8 cm，AB = 10 cm，求其内切圆的半径？应该怎么求？有几种方法？

1.求面积法。由以上条件，学生能够判断此三角形为直角三角形。根据“拓展一”的结论可知，它的面积既可用[12ab]（a，b表示直角边，c表示斜边）表示，又可用[12（a+b+c） r]表示，即ab = （a + b + c） r，由此得到求直角三角形内切圆半径的一般公式：[r=aba+b+c]。

2.求切线长法。有了直角这个特殊条件，引导学生继续观察思考。①四边形FCDO是什么图形？（正方形），能得到什么结论？（r = OF = OD = CF = CD）。②CD、CF是什么特殊线段？（表示切线长的线段）③应用前面的规律能得出什么结论？[r=CD=CF=a+b-c2]。

对r的两种求法都是建立在直角三角形条件之下的，这种特殊性的出现能够促进学生思维的转化，使学生更加充分地认识模型的本质和涵义，从而更好地培养学生“从一般到特殊”的数学思维觀念和推理能力。

这道常规例题经过一系列拓展整合，不仅让学生在知识上“能求三段相等的切线长，一般三角形与直角三角形内切圆的半径长”，而且在方法上“能用方程模型的思想解决图形问题，学会从一般到特殊、从特殊到一般的思考问题方法”。在一定程度上深化了学生认知，培养和训练了学生归纳、演绎等数学推理能力，学生思维的深度和广度得到提升。

三、“多变求同”，建立数形关系，培养几何直观能力

一题多变是数学学习中的普遍现象，通过动态思维寻求例题的多种变化。多变求同，并借助数形关系，在学生思维的最近发展区内进行多角度、多渠道探究，是例题教学的一种常态。

例如，在“二次函数与一元二次方程”教学时，利用函数图象求方程x2 - 2x - 2 = 0的实数根（结果保留小数点后一位）。因为图象与x轴交点横坐标为近似值，学生对此一元二次方程的图象解法感受不直观，理解也不深刻。另外，一元二次方程的图象解法不唯一，灵活多变，但万变不离其宗，方程的解不会改变。所以通过变换、补充等形式对此类例题进行改编，通过建立数形关系，让学生在多变中寻求不变，体会函数图象与方程的紧密关系，培养学生的几何直观能力。

1.变换方程。利用函数图象，求方程x2 - 2x - 3 = 0的解。此处变换方程的原因是此方程的解为整数。对应函数y = x2 - 2x - 3的图象与x轴交点横坐标为整数，如图10所示。

通过图象与x轴的交点横坐标与方程的解作对比，学生能直观地得到此方程的解为对应函数与x轴交点的横坐标，并能更好地理解它们之间的联系。

2.变形方程。对不同形式进行思考、演示、类比。

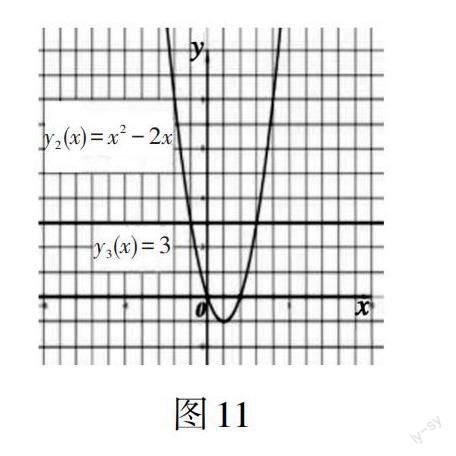
（1）教师引导。若把方程x2 - 2x - 3 = 0变形为x2 - 2x = 3，方程的解是什么？如何利用函数图象求方程x2 - 2x = 3的解？类比于“变换方程”中的思路，学生可以把此方程的解理解为函数y = x2 - 2x的图象与y = 3的图象交点的横坐标，并进行验证，如图11所示。

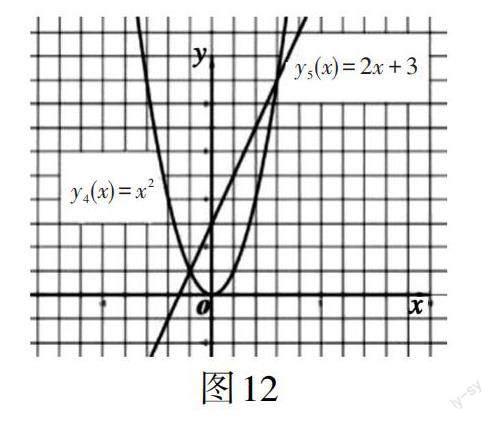
（2）学生创设。方程变形为x2 = 2x + 3，则它的解是否为y = x2的图象与y = 2x + 3的图象的交点横坐标？如图12所示。方程变形为x2 - 3 = 2x，它的解是否为y = x2 - 3的图象与y = 2x的图象的交点横坐标？能不能利用图象求y = x2 - 3与y = 2x所联立的方程组的解？这些猜想都要由学生自主创设，由教师利用几何画板进行验证。

此题设计意在引导学生建立数形关系，并从中发现同一个方程的解是不变的，但是它有多种变化形式，而每一种变化所对应的函数是不一样的。方程无论转化为何种形式，它的解都可以理解为两个对应函数图象的交点横坐标。而且通过这一建构过程，更好地夯实学生对一元二次方程图像解法的理解与掌握，培养发散思维，开拓解题思路，增强解题能力。

3.方程一般化。在学生有前面的认知和体验后，启发学生继续探究。给一个任意的一元二次方程ax2 + bx + c = 0，是否可以用不同的图象法求解？

继续探究的目的是让学生学到“从特殊到一般”的数学思想和方法，并能由此进行逻辑推衍，培养举一反三能力。

数学是思维的体操。在几何画板中，学生通过同一方程的不同变形，直观地感受函数与方程的关系。“一题多变”“多变求同”让学生认知重塑，思维放大，几何直观能力得到有效地提升。

四、“自主创设”，形成思维网络，培养分析归纳能力

新课标要求组织学生经历图形的分析与比较过程，引导学生关注事物的共性，形成合适的“类”。例题设计也要充分地考虑到共性问题，以“例”带“类”，通过对相关知识的梳理、整合，进行“自主创设”。

例如，二次函数图象中字母与系数的关系是学习二次函数重要内容之一，也是中考的高频考点之一，考点多，灵活多变，学生不易掌握；尤其在对图象认知、思考的过程中，学生得到的知识是散乱无序的，没有形成系统的知识结构，学生的思维空间是狭窄的，解题能力是有限的。其实，很多考题的设置都与二次函数的对称轴的含义有关，“对称轴”是解题的关键。在实际教学中教师要善于根据知识点之间的联系，引导学生找到二次函数的解题突破口——“对称轴”，深挖、细挖对称轴的含义，然后以它为主干，添枝加叶，联想其定义、轴对称性、最值等内容；再从学生的最近发展区出发，去激发学生的思维生长点，由此带出相关知识点及考点，有针对性地帮助学生对二次函数图象和性质等知识进行梳理、归纳，引导其建立起自己的思维导图，形成思维网络，提高分析归纳能力。

1.建立思维主干

如图13所示，对称轴x = 1，可得到哪些信息？引导学生把得到的信息进行归纳整理：

（1）定义。由x = 1既[-b2a=1]得b = - 2a，或[a=-b2，]或2a + b = 0。

（2）轴对称性。与x轴一个交点坐标是（3，0），根据轴对称性得到与x轴另一个交点为（ - 1，0），并把图象补充完整，如图14所示。

（3）最值。当x = 1时，二次函数有最小值，即ymin = a + b + c；

2.建立思维支干

由（1）定义得出的等量关系可以联想到哪些知识点？

联想一：不等关系，即有[-b2a=1]时，b = - 2a，则当[-b2a<1]或[-b2a>1]时，b与 - 2a有什么大小关系？在根据不等式性质进行变形时，要考虑a的正负，如本题中a > 0，则 - 2a < 0，所以由[-b2a<1，可得b>-2a;]

联想二：字母替换，对含有字母系数的代数式进行变形，即由b = - 2a，或[a=-b2，]可得a + b + c = - a + c，或[a+b+c=b2+c，]这可以解决含有两个字母系数或一个字母系数的代数式值的问题。

由（2）知道二次函数图象与x轴交点坐标，可得一元二次方程ax2 + bx + c = 0有两个不相等的實数根，分别是x1 = - 1，x2 = 3，进而根据图象上点的横纵坐标关系得a - b + c = 0，9a + 3b + c = 0。

由（3）可知y值中a + b + c的值最小，即当x = m （m≠1）时，函数值都比a + b + c大，所以可得a m2 + b m + c > a + b + c，即am2 + b m > a + b。

3.建立思维分支

如图14所示，由（2）支干继续观察联想：

联想一：由方程联想不等式，考察方程与不等式的区别与联系。已知ax2 + bx + c = 0的两个根为x1 = - 1，x2 = 3，那么不等式ax2 + bx + c > 0与ax2 + bx + c < 0的解集分别是什么？

联想二：由特殊值联想一般值，考察二次函数图象的连续性。已知x1 = - 1时，a - b + c = 0，x2 = 3时，9a + 3b + c = 0，那么x = - 2时，对应的函数值如何表示？如何通过图象去判断正负？x = 4呢？引导学生对4a - 2b + c及16a + 4b + c等相关代数式值的正负做出判断。

联想三：运用字母替换来变形字母代数式，考察字母系数相关代数式的多变性。由定义可知b = - 2a，所以得4a - 2b + c = 8a + c > 0；也可由[a=-b2]得4a - 2b + c = - 4b + c > 0，或c - 4b > 0。

因为（3）中函数的最小值还可以表示为[4ac-b24a，]所以在二次函数最值方面多角度去思考，如果顶点纵坐标为 - 4，则会得到a + b + c = - 4，或4ac - b2 = - 8a等相关等式。

由此，借助对二次函数对称轴的多层次、多角度思考，学生头脑中已经形成关于对称轴相对完整的知识体系，思维导图随之建立，如图15所示。

核心素养培养是教学目标，而例题教学是落实核心素养培养的关键一环，必须予以重视。在日常教学中，教师要立足核心素养，着眼例题优化设计，根据学生实际精选例题，不断地创新例题优化策略，使学生在体验数学发现和创造的过程中，训练思维，发展能力，实现学科育人价值。

[参 考 文 献]

[1]钟启泉，崔允漷.核心素养研究[M].上海：华东师范大学出版社，2018.

[2]黄世贵，刘贤虎.基于问题串从浅层走向深度：小学数学“分段计费”教学设计[J].中小学教学研究，2021，22（4）：86 - 91.

[3]刘海涛.基于核心素养的“问题链”课堂教学实践研究：以“基本不等式”第一课时教学为例[J].中小学教学研究，2021，22（3）：21 - 27.

（责任编辑：姜显光）