基于GeoGebra软件的立体几何数学实验*
李必船 何园园
(合肥市庐阳高级中学 安徽合肥 230000)
一、研究背景
现代意义的数学实验是以信息技术和专业数学软件的应用为特征,通过构建实验模型,在信息化和智能化环境中进行的探究型教学模式。实验过程中强调学生的独立操作和自主探究,有利于培养学生的创新精神,促进学生数学核心素养的发展,因而是一种适应课程改革与发展,体现立德树人精神的新型数学教学模式。所以,在中学数学课程中引入数学实验可谓是正当其时。
《普通高中数学课程标准(2017年版2020年修订)》强调数学教学要以六大核心素养为统领,其中“直观想象”是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,理解和解决数学问题的素养。主要包括:借助空间形式认识事物的位置关系、形态变化与运动规律;利用图形描述、分析数学问题;建立形与数的联系,构建数学问题的直观模型,探索解决问题的思路。
反思我们的教学,普遍存在不重视直观想象素养的培养问题,教师往往更愿意将时间花在逻辑推理和数学计算上,对于没有图形的例题,直接通过课件给出,然后再引导学生探究。这样的教学直接剥夺了学生训练直观想象素养的机会,也为其他素养的发展埋下隐患。为了调查即将升入高三的学生的直观想象素养,笔者将2022年高考数学试卷中的两道立体几何试题发给学生进行测试,从测试的结果看,学生的直观想象素养严重不达标,最直接的体现是不能根据语言描述绘制准确的图形,从而导致后续的逻辑推理和数学计算没有依托,成为空中楼阁。这引发了笔者对即将到来的高三数学教学的思考。
二、基于GeoGebra软件开展立体几何实验的可行性
(一)实验的理论依据
《普通高中数学课程标准(2017年版2020年修订)》指出:立体几何的教学重点是帮助学生逐步形成空间观念,应遵循从整体到局部、从具体到抽象的原则,提供丰富的实物模型或利用计算机软件呈现空间几何体,帮助学生认识空间几何体的结构特征,进一步掌握在平面上表示空间图形的方法和技能。所以,解决问题的关键是提供空间几何体的模型,模型的直观性一方面降低了思维的难度,另一方面提高了学生探究的有效性,避免部分学生陷入空想,增强学生的学习信心,提高探究的兴趣。
立体几何中的实物模型难以呈现空间几何体的动态变化,也难以保证让所有学生都能得到动手操作的机会,所以利用计算机软件建立数字化的模型就成为首选的方法。2019年版人教A版普通高中数学教科书推荐的GeoGebra软件是一款专业的数学软件,其3D视图功能可以实现空间几何体的动态演示,是立体几何教学的好帮手。该软件是一款跨平台的免费软件,可以安装在各种电脑、手机和智慧课堂的平板电脑中,为实现立体几何实验提供了可靠的工具。
(二)实验的硬件设备
智慧课堂系统为实验操作、成果提交、交流和讨论提供了便捷的平台,教师在系统中发布实验任务,学生在平板电脑上进行实验操作,得到实验结果后通过截图提交成果,提交后即可在班级中进行展示与交流,通过与其他同学的实验作品进行比较,学生可以获得更多的实验感受。交流与展示可以由教师在大屏幕上进行点评,还可以通过智慧课堂系统中“学生讲”的功能实现,它能够让学生的平板投屏到教室的主屏幕上,学生只需在自己的平板电脑上操作就可以在全班展示实验操作与实验结果。所以,智慧课堂系统是理想的实验平台。
(三)实验的教学模式
基于GeoGebra软件的立体几何实验模式的基本内容包括制订实验目标、制订实验内容、制订实验步骤、建立实验模型、学生自主实验、提交实验结果、实验原理分析与验证、实验总结与拓展。
实验目标和内容要有明确的核心素养导向性,要处理好与数学常规教学的关系。作为数学课程的有机组成部分,数学实验课为学生提供了动手实践、动眼观察、动脑思考的时间和空间,是常规课堂教学有益的补充,重点是在真实的情境中通过循序渐进的训练提高学生运用信息技术解决数学问题的能力,提高数学核心素养。实验步骤要追求简洁性和确定性,避免因为操作步骤烦琐而造成时间上的过度消耗,使教学方向出现偏差,影响教学目标的实现。实验步骤的确定性是有效教学的重要保证,步骤的设计要反复推敲,考虑各种可能,既要保证学生在实验操作中的创造性,又要保证能得到准确的实验结果。
实验模型的建立有两种形式,对于平面上的函数与几何问题,应该以学生自主建立模型为主,既提升学生的信息技术素养,又提高实验过程的完整性;包括立体几何在内的其他实验,以教师建立实验模型后分享给学生的形式为主,提高实验的有效性和准确性。
实验结果的交流展示与实验原理分析以学生讲评和讨论为主,教师做好串联、并联与总结,改变填鸭式的教学方式,推进探究式的教学,这是核心素养目标实现的关键环节。实验原理的验证环节是指学生运用数学知识、方法与技能,建立问题的数学模型,进行逻辑推理与数学计算,从理论上检验实验结果的正确性。因为已经通过实验感知到几何元素之间的依存关系,学生能够在较高的层面上理解问题的本质,为使用数学方法验证结论提供了素养方面的支持,验证结论的过程也是数学素养锻炼与提升的过程。
数学实验要实现上述目标,绝不是一两节课就能够实现的,学生的实验操作能力、教师的实验设计与实验教学能力都需要通过多次的实践才能提高。所以,数学实验不能流于表演,要落到实处,形成稳定的校本课程,才能真正发挥实验教学对于核心素养的提升作用。
三、基于GeoGebra软件开展立体几何实验的案例研究
(一)高考试题呈现
2022年全国乙卷理科数学第9题(文科第12题):已知球O的半径为1,四棱锥的顶点为O,底面的四个顶点均在球O的球面上,则当该四棱锥的体积最大时,其高为( )

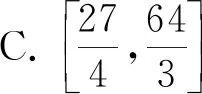
这两道试题属于立体几何中的典型试题,基于棱锥和球面考察学生的空间想象能力、逻辑推理能力和数学计算能力。从课程标准的角度看,这两道试题的解决步骤完美呈现了课标的要求,第一步是借助直观图认识棱锥与球的位置关系、形态变化,学生需要根据语言描述绘制直观图;第二步是利用直观图或轴截图建立形与数的联系,构建几何问题的函数模型,确定棱锥的底面外接圆的半径与球的半径满足的关系;第三步是对函数模型进行计算,运用导数求出函数模型的最值,得到几何问题的答案。
参试学生中有约30%的学生因不能正确画出直观图而导致失分,在能画出直观图的学生中,只有约60%的学生能够正确分析几何元素的关系,推出棱锥的底面外接圆的半径与球的半径满足的关系并建立函数关系式。所以,较高的直观想象素养是发现和提出问题、分析和解决问题的重要前提,是探索解题思路、进行数学推理、构建数学模型、形成数学结论的思维基础。
(二)实验设计整体思路
数学实验内容的选择要体现数学的抽象性,不能局限于一题一例,好的实验内容应该是以解释一类现象为目标的综合性问题,背景比较复杂,通过实验抽象出数学模型,数学模型在不同的条件下产生不同的实验结果。数学六大核心素养是一个有机的整体,解决综合性问题最能体现核心素养的水平,对核心素养的提升作用也最显著。
事实上,各种棱锥的外接球问题大多可以转化为圆锥的外接球问题,如2022年高考全国乙卷理科数学第9题中的四棱锥的体积问题可以转化为图1中圆锥OO′的体积问题,2022年新高考数学Ⅰ卷第8题中四棱锥的体积问题也可以转化为图2中的圆锥PO′的体积问题,只需要求出棱锥的底面外接圆的半径就可以实现转化。所以,本案例的实验模型主体为球的内接圆锥,其一般性体现在两个方面:一是圆锥的顶点和底面可以通过拖动实现变化,让学生在真实的环境中直观体验几何体的演变过程。二是可以在圆锥内构造各种正棱锥,其底边边数通过一个整数型滑动条n控制,如图1是四棱锥,图2是三棱柱,以提高实验的普适性,还可以呈现当边数n→+∞时,棱锥趋近于一个圆锥的过程。

图1
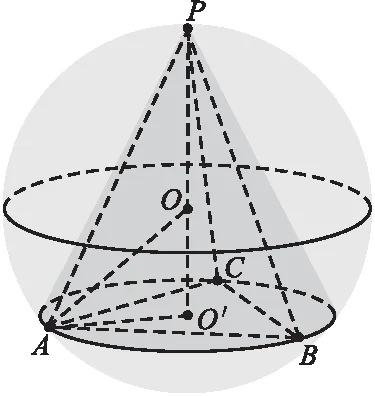
图2
数学实验的设计还要体现数学的严谨性,通过观察获得结论的正确性,需要通过逻辑推理和数学计算进行验证,所以,实验设计不能仅限于观察,还要有分析原理和验证结论的环节。
基于以上的分析,本案例的整体思路是利用GeoGebra软件制作实验模型:球的内接圆锥和内接棱锥,其中圆锥PO′的底面圆在球面上运动,正n棱锥(底面边数n可通过滑动条控制)的底面顶点在圆锥的底面圆上。
实验活动甲:如图1所示,当顶点P与球心O重合时,观察并验证圆锥和棱锥的最大值。
实验活动乙:如图2所示,当顶点P在球面上时,观察并验证圆锥和棱锥的最大值。
(三)建立实验模型
第1步:在“3D绘图区”作点O=(0,0,0),以O为球心、半径为1作球面a,以O为圆心,作半径为1的圆c。
第2步:在z轴上作点O′,过O′点作与z轴垂直的平面p,与球面交于圆d,隐藏平面p。
第3步:在“2D绘图区”建立整数型滑动条n,取值范围为[3,10]。在圆d上任取一点A,以z轴为旋转轴,将点逆时针旋转(360/n)°,得到点B。作以A、B为顶点,边数为n的正多边形poly1。拖动滑动条n可以改变圆d的内接正n边形的边数。
第4步:在z轴上取一点P,以多边形poly1为底面,P为顶点建立棱锥b。
第5步:以O′为底面圆心,P为顶点,线段O′A为底面半径建立圆锥e。
第6步:连接线段OO′、线段OP、线段OA、线段O′A,隐藏坐标系。
(四)实验过程设计
1.实验活动甲:顶点与球心重合的圆锥和棱锥
(1)实验操作:将n的值设置为4,P与球心重合,得到四棱锥P-ABCD(四棱锥b)和圆锥PO′(圆锥e),在球O内拖动点O′改变棱锥和圆锥的形状。
(2)实验观察:通过观察,说出四棱锥b与圆锥e的体积的最大值。
通过实验与观察获得结论:如图3和图4所示,在实验模型中拖动圆锥的底面圆心O′可以实现圆锥和棱锥的连续变化,图3中的棱锥和圆锥体积较小,将O′向上拖动时棱锥和圆锥的体积逐渐增大,到图4的位置时,体积分别为0.26和0.4,再向上拖动O′点时棱锥和圆锥的体积逐渐变小,所以四棱锥b体积的最大值是0.26,圆锥e体积的最大值是0.4。
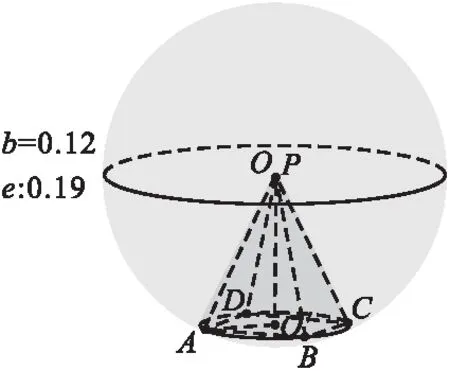
图3

图4
(3)数学建模:已知球O的半径为1,设圆锥PO′的底面半径为r,请结合实验模型推出四棱锥b的体积V1和圆锥e的体积V2。

数学建模是最高层次的数学核心素养,通过实验设计,为数学建模问题提供一个直观的观测和实践平台,利于学生领悟问题的本质、建立元素之间的整体联系。通过循序渐进的实验步骤,将复杂的问题转化为一个较为简单的“问题串”,学生通过“问题串”形成的思维阶梯可以到达思维的最高一级。较高层次的数学素养不是一朝一夕能够实现的,循序渐进、螺旋式上升才是正确的途径。
(4)验证结论:

因为f′(t)=2t-3t2=t(2-3t),

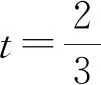

结论的验证就是基于数学模型进行逻辑推理和数学计算,因为有实验的辅助,推理和计算的过程不再抽象和枯燥,难度相对降低。对比来看,上文引用的高考题如果采用常规的教学方式进行分析讲解,大部分学生能够掌握,但缺乏举一反三的能力,因为习题教学往往难以延伸扩展,对学生解决一般性问题的素养提升作用有限。采用实验方式进行教学的优点是学生能够体验到更多的情况,学生的理解程度和素养提升幅度比常规教学更大。
2.实验活动乙:顶点在球面上的圆锥和棱锥
(1)实验操作:将n的值设置为3,P在球面上,坐标为(0,0,1),在球O内拖动点O′改变棱锥和圆锥的形状。
(2)实验观察:通过观察,说出三棱锥b(三棱锥P-ABCD)与圆锥e(圆锥PO′)的体积的最大值。
实验结论:如图5所示,三棱锥b体积的最大值是0.51,圆锥e体积的最大值是1.24。
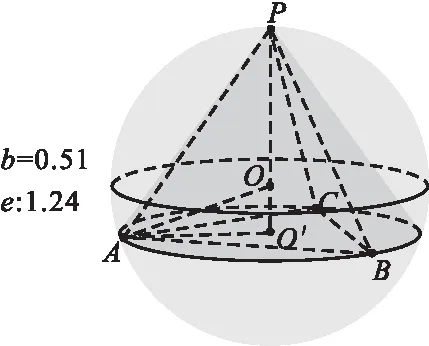
图5
(3)数学建模:已知球O的半径为1,设圆锥PO′的高为h,请用h表示三棱锥P-ABCD的体积V1和圆锥PO′的体积V2。
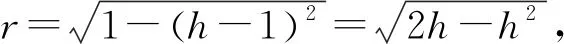
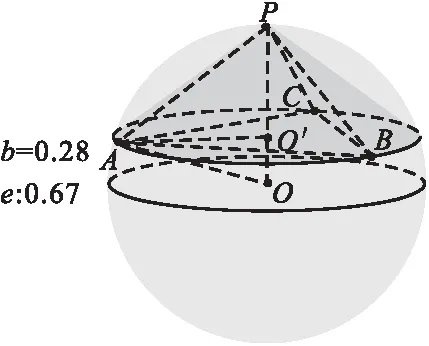
图6

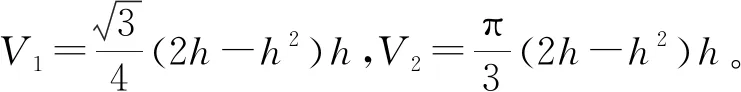
(4)验证结论:
V1和V2可以用函数f(h)=2h2-h3(0 因为f′(h)=4h-3h2=h(4-3h), 实验最后,可以留给学生一个课后的拓展性问题:如果圆锥的顶点在球半径的中点呢? 实验是数学教学的重要形式,是常规教学的必要补充,对于提高教学质量、提升学生数学核心素养有不可替代的作用。数学实验要与信息技术深度融合,考虑学生的差异性,设计合理的实验目标,实验中加强对学生的引导和个别指导,实现真正的手眼脑并用,避免流于形式的表演。立体几何实验模型的制作费时费力,需要教师学习新的软件和技术,这既是教师的职业要求,也是教师的成长之路。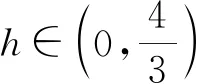


四、结语

