有关教育增值分析模型的应用研究*

穆明

淄博市基础教育研究院 山东淄博 255030

0 引言

“改进结果评价、强化过程评价、探索增值评价、健全综合评价”是《深化新时代教育评价改革总体方案》提出的一项重要的任务，在落实这项任务时，一线教育评价工作者遇到不少挑战，其中的难题之一就是如何实施增值评价测量。笔者在工作实践中，通过对众多教育增值评价案例的对比分析，在掌握统计学理论的基础上，对教育增值分析模型进行了研究，并借助HLM 软件对教育增值进行了精准测量。故此，本文对基于纵向数据的教育增值测量常用模型进行分析，抛砖引玉，以期为一线从事教育测量与评价的同仁深入理解应用增值评价模型提供参考。

1 教育增值的概念与测量方法

教育增值的概念是建构于学校为其学生成绩增加“价值”的假设之上的，其基本思想是测量学生经过一段时间后的进步，需要在一段特定时间的开始和结束时刻测量基线和结果，测量学生学业进步的最关键证据是一段特定时间内的基线和最终成绩数据，当然也可以需要学生个人和学校的其他背景和环境信息。由于学生的自身成长，按正常预期学生都会有进步或改进，平均成绩随之会提高，鉴于此，学校增值界定为在学生可预期的正常成长之外，由教育所带来的额外价值，由此增值评价要考查学校的学生在一段特定时间内是否比其他学校的学生取得相对更大或更小的进步，即为超过预期的学校效能。基于对增值概念的正确理解，学校效能增值并非为学生个体增值，非起始时刻的基线成绩也不必作为协变量引入增值分析模型中。

遵循统计学理论能够分离学校经历和学生原有特征作用于学生个体成绩的统计方法，根据基于的统计技术不同带来的分析灵敏度和复杂度的不同，对教育增值的测量主要归纳为三种主要的方法。

1.1 概要统计

概要统计用来从学生水平数据中计算学校总体水平，通过估计样本中每所学校学生成绩的原始水平，提供学校表现的简单情况。此方法的缺点是不能估算学生的进步，因为是以学校为分析单元，在分析中会损失学生个体的详细信息。

1.2 多元回归分析

多元回归分析是计算观察分数与预期分数残差的标准统计技术，在测量学生进步时，观察分数是一个学生的实际成绩水平，预期分数是其先前基线成绩基础上预测的水平，残差分数用来解释一个学生的表现是高于还是低于预期。这种方法的缺点是分析单元只能是学生水平（即计算学生残差分数的位置）或学校水平（即计算学校残差分数的位置）之一，前一种情况损失了特定学校中学生群体的重要信息（忽视了学校的汇聚作用），后一种情况损失了学生个体的详细信息。

1.3 分层线性模型

分层线性模型是线性回归的拓展和延伸，其计算残差增值分数的原理与多元回归相同，但是，此技术兼顾了嵌套在学校中的学生群体，允许分析单元同时包括学生和学校水平，充分考虑了上层组织的汇聚作用，在分离学校效能时，多水平模型是一种比概要统计和标准多元回归更成熟的方法，应用此方法可以无偏估算学生群体的学校残差，更重要的是检验单个学校结果的统计显著性。

在学业评价增值分析中常用到组织模型和发展模型，两种模型均能体现上层单位如学校的汇聚作用，以此进行上层单位的增值效能分离。针对单一学生年龄群体在收集、记录基线和结果评估的数据时，需要保证个体学生的记录能在以后都能准确匹配，以此为样本建立的模型为组织模型；针对考查跨时间的趋势或在增值表现中的改进，需要收集至少三个连续时间点学生群体的相同结果和基线数据，以此为样本建立的模型为发展模型。在计算学校表现的增值测量时，一般不需考虑教育和学校的过程信息，因此，在进行教育增值测量时，不必引入教育和学校发展过程中的变量因素来实现拟合学校增值的主效应。

2 分层线性模型理论

分层线性模型的建模基本思想为：一是将分层结构数据在因变量上的变异分为组内变异与组间变异两个层次（随机误差方差与参数方差）；二是分别在不同层次上引入自变量对二者进行解释（也可只在其中一层引入协变量）。

如以区域内学校学生的学业成绩建立的二层线性模型为例：组内（层1）模型对同一所学校学生的学习成绩进行线性回归，取得不同学校线性回归方程的模型参数（截距与斜率）估计值；组间（层2）模型分别以层1 模型的线性回归模型参数（截距与斜率）作为因变量进行回归。

分层线性模型可理解为对组内（层1）模型的回归截距与斜率系数的再回归，根据模型方程的表达形式（矩阵或标量）通常应用迭代广义最小二乘法或迭代加权最小二乘法进行模型参数优化，采用HLM 分层线性模型统计软件进行参数估算及显著性检验[1]。

分层线性模型不是一个单一模型，其包括了从最简单到最复杂的多个子模型。与教育增值分析研究相关的基础模型有：零模型、随机截距模型（协方差分析模型）、随机系数回归模型。其中随机截距模型可视为随机系数回归模型的特例。零模型和随机系数回归模型的建模原理阐释如下。

2.1 零模型

零模型也称为空模型，是最简化的分层线性模型，虽然不能直接用来进行分层数据分析，但它是构建分层线性模型分析的起始点。零模型的层1（组内）模型与层2（组间）模型都不包含解释变量。其数学模型为：

层1 模型：yij=β0j+εij

层2 模型：β0j=γ00+μ0j

其中，γ00是样本总体中因变量的平均值，μ0j是与第j个层2 单位相关联的随机效应。

将层2 模型代入层1 模型可得组合模型：

yij=γ00+μ0j+εij

在零模型中结果变量的方差由组间方差与组内方差两个部分组成，根据零模型估算的随机系数方差和随机误差方差，可进行组内相关系数的计算：

ρ=τ00/(τ00+σ2)

其中，σ2为组内随机方差，τ00为组间参数方差。

ρ值表示层2 单位之间的差异在层1 结果变量的总方差中所占的比例。如果ρ值很小（通常小于0.059），说明层2 单位之间的差异不大，不需要采用分层线性模型，采用常规的一元或多元线性回归方程进行统计建模就可以进行统计分析，如硬性采用分层线性模型可导致统计数据的不精确；反之，则需要采用分层线性模型。通常在应用带有协变量的分层线性模型进行统计分析之前，一般都需要建立零模型来进行判断是否需要采用分层线性模型。

2.2 随机系数回归模型

随机系数回归模型是完整分层线性模型的最简形式，它在零模型的基础上，将层1 模型的截距和斜率系数设定为在层2 单位之间是随机变化的，但层2 模型不引入协变量对层1 模型的截距与斜率系数中存在的变异进行解释。与随机系数模型密切相关的一项统计技术是协变量的测量定位，一般采用对中方式,对中在分层线性模型中具有非常重要的作用。在经典的协方差模型中通常选择基于总均值对中,即采用标准测量方法。其数学模型为：

层1 模型：yij=β0j+β1j(xij-)+εij

层2 模型：

β0j=γ00+μ0j

β1j=γ10+μ1j

其中，γ00是层2 模型所有层2 单位的回归截距的均值，γ10是层2 模型所有层2 单位的回归斜率的均值。μ0j、μ1j分别是层2 模型在回归截距和回归斜率上与第j个层2 单位有关的特性增量。

将层2 模型代入层1 模型，可得组合模型：

τ00表示层1 所有截距假定服从先验正态分布的无条件方差，τ11表示层1 所有斜率假定服从先验正态分布的无条件方差，τ01表示层1 所有截距与斜率的无条件协方差。在对回归截距均值γ00和回归斜率均值γ10的估计值进行统计检验（t检验）为显著时，说明研究总体中的固定效应不为0；同样对随机效应参数μ0j与μ1j进行统计检验（卡方检验），如果无法拒绝二者都等于0 的原假设，就意味着研究总体中的各单位的层1 系数大致相等，即为固定值不存在随机变化，可取消层2 单位中的随机项μ0j与μ1j。

随机系数回归模型的误差项包括三部分：

εij为层1 误差；

μ0j为层2 截距模型的误差；

μ1j(xij-)为层2 斜率模型的误差μ1j与层1 协变量的乘积。

层2 单位的平均效能（用μj表示）为组合模型的总残差减去层1 的平均随机误差的剩余部分，因层1 随机误差的不可测性，根据经典测量真分数理论的数学模型，故定义层2 效能方差（层1 真值方差）与总残差方差（样本均值总方差）的比率为可靠性系数（λj）即信度，用可靠性系数（信度）与总残差的乘积作为层2 单位的效能，从而分离提取层2 单位的增值量。

3 模型案例分析

分层线性模型的一项重要的应用就是检测单个组织效应，其常见的应用大致分为在组织研究中的应用和个体变化研究中的应用，有关组织如何影响个人的问题可采用组织模型实现，有关多个时点上个体变化现象的问题可采用发展模型实现。

3.1 组织模型

对学校增值的测量是以该校学生的背景和基线能力而预测的平均成绩为回归数据值，如果实测学校平均成绩分值高于此预测值，这样的学校被认为是好学校。每个学校的效能增值指标可以从其实测平均成绩与其预测的平均成绩的差中分离提取。考虑到残差效应估计值的稳定性，出于追求统计有效和计算稳定性的目的，通常采用经验贝叶斯估计方法，能够提供判定测量学校增值的稳定指标，借鉴国内外增值评价成功案例的增值效能算法，优选采用随机截距模型进行学校增值分析。另外，在计算学校表现的增值量时，一般不用教育和过程信息，常用的学校业绩增值分析模型为随机截距模型，它是完全模型的一个特例。其数学模型为：

层1 模型：yij=β0j+β1j(xij-)+εij

层2 模型：β0j=γ00+μ0j

将层2 模型代入层1 模型，可得组合模型：

yij=γ00+β1j(xij-x)+μ0j+εij

类似“水涨船高”的原理，因学校j的所有学生都在该学校上学，所以都有一个增值效应μ0j叠加到他们的预期回归分值上，j个学校在单因素随机效应协方差分析中构成为独立的组，模型的实现目的是提取每个层2 单位效应的估计值。每个学校的OLS（最小二乘法）估计效应为：μ_j是协方差分析中的校平均残差，对于样本少的学校产生的μ_j估计值不稳定。为此，采用分层线性模型的经验贝叶斯残差作为学校效应估计值（用μj表示），用前文提到的可靠性系数（λj）作为提取因子，计算公式为：

μj=λjμ-j

其中：

λj=τ00/[τ00+σ2/nj]

根据贝叶斯推断理论，在给定学校的平均成绩后每个学校的随机效能μ0j的后验分布都服从均值为μj，方差为Vj的正态分布[2]。

其中：

Vj=1/[1/τ00+nj/σ2]

据此可以估计μ0j的95%置信区间（可能值域）：

μj±1.96Vj1/2

通常只有置信区间的最大值在0 值以下的，表明学校效能低于平均水平，通常只有置信区间的最小值在0 值以上的，表明学校效能高于平均水平，置信区间包含0 值的表明学校效能并无统计学意义上的差异。因此，可以借助置信区间来实现增值结果的呈现，根据置信区间的端点值进行学校效能分类，达到学校对数据的所有权和保证结果的保密性要求。

作为组织模型应用研究实证案例，以淄博市2022年高三数学模考（入口成绩）和一模（出口成绩）成绩进行分析建模，将两次成绩进行线性等值处理后，以学生为层1、学校为层2 建立两层线性模型，先建立空模型进行可行性分析。空模型检验结果如表1所示。

表1 空模型检验结果

由零模型估算的跨级相关系数（ICC）达到47.59%，说明47.59%以上的总变异是由层2 学校之间的差异引起，也即学校的差异是影响成绩的主要原因，因此，必须建立分层线性模型进行统计分析，所建立的随机截距模型检验结果如表2所示。

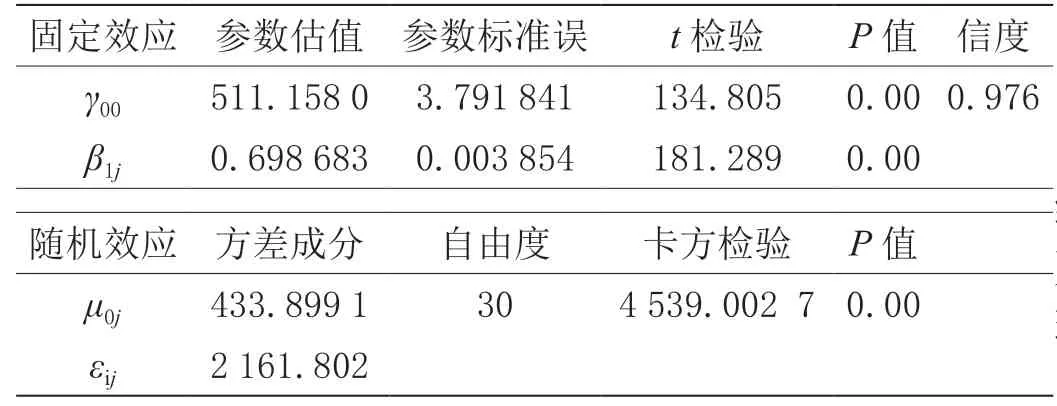
表2 随机截距模型检验结果

3.2 发展模型

为了考查跨时间的趋势（效能）或在增值表现中的改进，需要建立把多次观察结果作为时间的某种数学函数的模型，即发展模型。本模型的输入为学校的平均成绩，过程是时间变量，结果输出学校的平均成绩增值效应。通过对连续几个年度（至少3 个年度）的学校平均成绩建模，实现测量每个学校在年度变化中的进步程度。基于所采集到的数据，建立包含时间和学校变量的分层线性模型。作为发展模型应用研究实证案例，以淄博市连续3年中考平均总分建立随机系数回归为例，两层数据分别是第一层的时间水平和第二层的学校水平。模型为：

层1 模型：Yti=π0i+π1i*yearti+εti

层2 模型：π0i=β00+γ0i

π1i=β10+γ1i

组合模型：

Yti=β00+β10*yearti+γ0i+γ1i*yearti+εti

其中，Yti代表学校i的第t 时刻考试平均分，对时间变量2019年、2020年、2021年的编码可以为0,1,2。εti为学校i的第t 时刻与线性回归的离差（随机误差）。

t 时刻残差、方差为：

eti=γ0i+γ1i*yearti+εti

Var(eti)=τ00+2yearti*τ01+yearti²*τ11+σ²

由学校引起的差异效能计算：鉴于要比较学校不同年度之间的增值这一目的要求，基于发展变量的线性模型，学校的某年度总残差由学校给定年度线性回归当年度（层1）的随机误差εti与学校（层2）之间因教育发展引起的差异γ0i+γti*yearti两部分组成。由学校发展引起的残差即学校效能可靠性系数（信度）为：

λ t i=τ00+ 2 y e a rti τ01+ y e a rti²*τ11/τ00+2yearti*τ01+yearti²*τ11+σ²

i学校某年度的净效能提取公式为：μti=λtieti

i学校t 时刻相对零时刻的效能增值=μti-μ0i

作为发展模型应用研究实证案例，以淄博市连续3年（2019—2021年）中考平均成绩进行分析建模，将3 个年度的中考平均成绩进行线性等值处理，如表3所示。

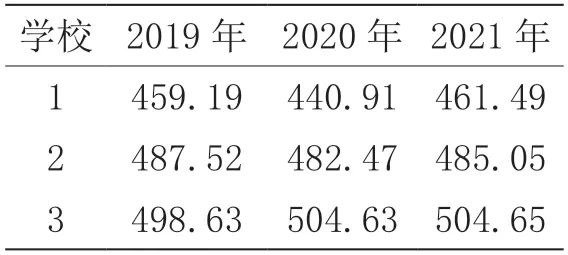
表3 淄博市中考成绩等值分

先建立空模型进行可行性分析。空模型检验结果如表4所示。

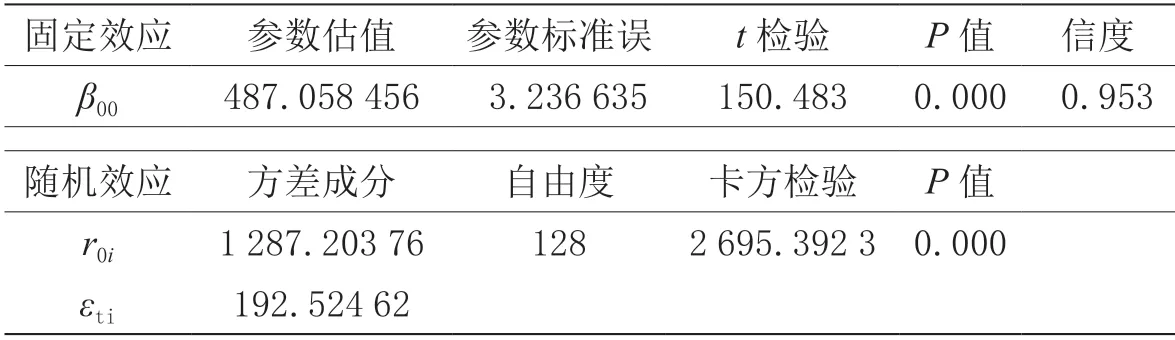
表4 空模型检验结果

由零模型估算的跨级相关系数（ICC）达到86.99%，说明86.99%以上的总变异是由层2 学校之间的差异引起，也即学校的差异是影响中考成绩的主要原因。因此，必须建立分层线性模型进行统计分析，所建立的随机系数回归模型检验结果如表5所示。

表5 随机系数回归模型检验结果

从固定效应看出，初始时刻（2019年）的学校平均分（截距）回归值为489.812，斜率系数为-2.753 834，检验结果达到显著性水平（P＜0.05），层1 的误差变异为143.590，说明学校在每年中考成绩之间的变异程度较大。

从随机效应看出，截距和斜率在不同学校之间的变异非常显著（χ2值分别为1 424.171 和203.299），说明学校之间在初始年度平均分和不同考试年度间变异比较明显，并且从方差成分的大小可以看出，变异主要发生在截距上，即学校在初始年度平均分的变异远大于不同考次之间的变异。从层1 系数的信度估计结果来看，截距项估计的信度比较高（0.910）。一般来讲，如层1 方程某系数的信度较小，在进一步的分析中可以把它设为没有随机成分的固定参数。最后进行历年中考学校增值比较分析：随机抽取某区县的3 所学校作为分析样本对2019—2021年学校中考平均成绩的增值情况进行评估，增值评估数据结构如表6所示。

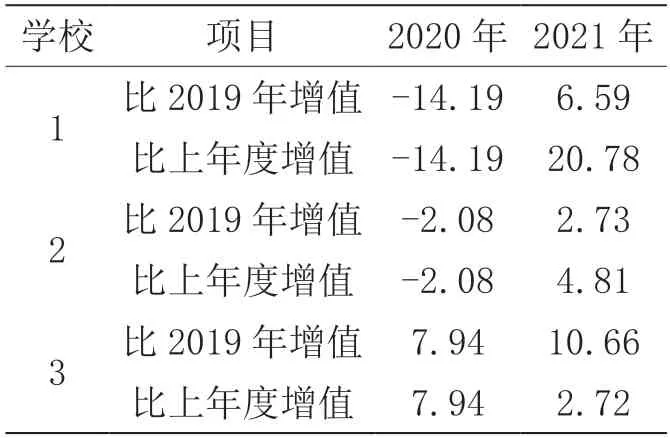
表6 区县学校的增值评估数据表

4 结束语

总之，分层线性模型是当前教育测量处理增值评价问题的最新技术，随着教育评价和教育督导关于学校增值评价政策措施的进一步出台及落地实施，学校增值指标必将作为学校评价与自我评价的有效工具，参照本文提供的增值分析测量模型，可以为教育增值评价的有效实施提供可借鉴的思路。