一种风向监督双流神经网络——以一维Burgers方程求解为例*

耿浩冉, 田 浩, 王成龙, 宋 宁, 魏志强, 冯毅雄, 郭景任, 聂 婕**

(1. 中国海洋大学信息科学与工程学部, 山东 青岛 266100; 2. 中国海洋大学数学科学学院, 山东 青岛 266100;3. 浙江大学机械工程学院, 浙江 杭州 310058; 4. 深圳中广核工程设计有限公司, 广东 深圳 519000)

近些年来,众多科研人员对偏微分方程数值求解工作进行了研究,其中Burgers方程作为描述流体动力学过程的模型有着一定的优势,首先Burgers方程包含了具有平衡作用的雷诺数,以及粘性项等元素,已经作为典型方程应用于各个领域;其次Burgers方程作为Navier-Stokes方程的简化数学方程,纳维斯托克斯方程删除压力项以及外力项后与Burgers方程高度相似,在实践方面具有重要意义。在计算流体力学中,迎风格式[1]作为求解偏微分方程的一类数值离散方法得到了广泛的应用。长期以来许多研究人员对Burgers方程的求解方法进行了研究,目前传统的偏微分方程数值求解方案主要包括有限差分法[2-3]、有限体积法[4]、有限元法[5]以及谱方法[6]等,这些方法的提出有效地推动了偏微分方程求解工作的发展。但是以上方法总是在计算速度与精度之间存在权衡,求解精度越高,计算成本越大。还有部分学者在有限体积框架下提出了基本无震荡(ENO)方法[7-8],其中ENO方法主要分为两类:单元平均型和通量型,前者主要是通过自适应地选取插值节点,再采用拉格朗日(Lagrange)插值来对边界通量进行逼近;后者则是在此基础上引入了龙格-库塔(TVD-Runge-Kutta)时间离散的思想,该方法的重点主要在于空间处理过程。由于ENO方法存在大量的逻辑判断过程,可能会导致收敛速度缓慢,计算效率低下等问题,因此有学者在ENO的工作基础上提出了加权本质无振荡格式(WENO格式)的思想[9],该方法作为一种重构或插值过程可以有效地应用于有限差分以及有限体积格式中进行求解,此方法主要是通过引入加权因子,同时保持了ENO格式的分辨能力,以此提高截断误差的阶数,进一步提高了计算效率。Guang-Shan以及Youngsoo等[10-11]开发了一种新的WENO方案,称为WENO-JS。有研究学者基于三阶WENO方法与先验知识相结合进行求解Burgers方程[12],有效的捕捉了数值解的结构,同时最大程度上避免了激波附近伪振荡现象的产生,从而提高了计算效率。

随着工业领域的快速发展,传统数值求解方法在计算网格上获得收敛解所花费的时间成本巨大,因此计算速度是亟需解决的问题。有研究团队在传统数值求解方法的基础上展开了研究,对多重网格技术也燃起了兴趣。在20世纪70年代,有研究学者开始通过使用多重网格提高复杂区域网格化流动问题的收敛速度。Vsparis等人最初得到了跨声速势方程的第一个多重网格流动解[13],多重网格方法也因此开始应用于各种结构网格求解器中。Caughey D,Mavriplis D等专门将中心差分方法与多重网格结合开始进行多重网格求解器工作的研究[14-17],这项工作也成为了多重网格求解器工作的重大突破。

目前流体的数值模拟在模拟诸多物理现象时起着不可替代的作用,大规模求解方程却存在着不小的挑战。Jiawei Zhuang等[18]开始将数据驱动离散化思想应用于湍流中被动标量的一维或二维平流方程的研究中,该工作首先在一维平流中使用神经网络学习平流方程中的有限差分系数,使得预测解与真实解尽可能地匹配,在一维和二维的平流测试工作中均获得了较为完美的结果,而传统的数值求解器则发生了明显的扩散误差。为了更好的改进计算流体动力学中的近似值,以高质量完成对二维湍流的建模工作,Dmitrii Kochkov等[19]研究了一种新型数据驱动的数值方法,该方法有效的扩展了计算流体动力学中的模拟边界,可以使得在粗糙分辨率网格上仍然可以获得与传统有限差分方法同样的精度,它可以很好的适用于不同的函数。Ameya D等[20]、Rodriguez-Torrado R等[21]先后提出了保守物理信息神经网络(CPINN)以及基于注意力的物理信息神经网络(PIANNs),他们在不同角度进一步提高了物理过程建模的准确性,打破了以往工作所存在的局限性,有效提供了一种高质量的物理过程建模解决方案。

在以上工作基础上,国内外研究者开始基于神经网络的偏微分方程进行求解工作的研究,受到了很大启发并提出了突破性方法,如基于物理驱动与数据驱动相结合的偏微分方程求解方法。Raissi 等[22]通过将神经网络与物理信息方程相结合,构造出一种新的求解高效的函数求解器,可以将物理定律转化为物理先验信息,有效的提高了求解速度。在此基础上,机器学习与传统数值求解方法结合的工作取得了一定的进展[23-26],在保持原有求解精度的同时提高了计算速度。O. Obiols-Sales等提出了一种耦合的深度学习物理模拟框架[27],实验结果表明此框架可以有效加速Navier-Stokes方程模拟的收敛。Bar-Sinai 等[28-29]使用数据驱动的思想来解决代价高的问题,以获得更高的收敛速度和准确性。他们主要通过将神经网络模型嵌入到偏微分方程求解的复杂步骤,以代替偏微分方程求解过程中系数求解部分,空间导数以及时间导数的计算仍然使用传统的数值求解方法,它允许求解是端到端的优化的过程,此工作在小尺度的网格下进行模拟并应用到大尺度的网格,在Burgers方程、KDV方程以及KS方程上进行了实验并获得了不错的结果,但是该工作只能应用在指定的方程中。对于方程的微分环节,Bar-Sinai的工作中使用了Bradbury等所提出的JAX框架[28],该框架本质上是一个函数转换的高性能数值计算库,支持任意数值函数的前向和反向模式的自动微分。

虽然以上工作均取得了一定的进展,但是这些方法仍然存在着以下不足:在数据驱动离散化建模过程中通常未考虑迎风格式对求解精度的影响;对于上下风向节点的信息平等对待,难以充分考虑不同阶段风向对系数的影响比重,无法有效获得各节点间关联信息。

针对以上不足,本文提出并设计了风向监督双流神经网络以及风向判断模块,实现了对预测得到有限差分系数的权重融合。通过风向监督双流神经网络,并结合先验知识对学得的系数分配一定的权重,以突出上下风向对预测结果的不同影响,可以有效实现对不同风向上的点分别进行预测,使得空间结构特征信息挖掘更加充分,从而提高差分系数预测的精度。

1 风向监督双流神经网络

该部分将从整体系统架构、卷积神经网络及结构、风向判断模块以及损失函数对模型的整体架构展开论述。

1.1 风向监督双流神经网络架构

本篇论文的风向监督双流神经网络架构如图1所示。Burgers方程最初用作对流与扩散之间相互作用下的建模工作,此方程将波动方程与热传导方程相结合,并且具有守恒定律、非线性方程等特点。此外,Burgers方程与纳维斯托克斯(Navier-Stokes,N-S)方程有着密切的联系,纳维斯托克斯方程删除压力项以及外力项后与Burgers方程高度相似,而N-S方程是描述天气、洋流、航天飞行器物理过程的关键方程组,这也使Burgers方程有着很高的研究价值。此工作先将该方法在Burgers方程上进行验证,在未来工作中会将该方法推广至纳维斯托克斯方程等复杂的方程组求解中,以更好的实现天气、洋流、飞行器气流等预测工作。对于Burgers方程(公式(1)所示)求解的标准流程在架构图中由浅蓝色框表示。

(1)

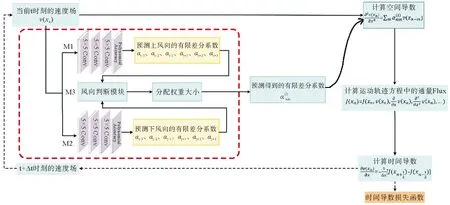
图1 风向监督双流神经网络图

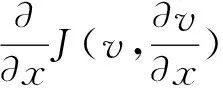
(2)

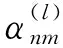
(3)

(4)

针对本论文中的空间离散化方案,设计了如架构图1中红色框所显示的内容。该部分主要包括三部分,其中M1与M2是风向监督神经网络部分,M3为风向判断模块。M1和M2模块分别考虑上风向和下风向对速度场的影响,利用卷积层分别提取受不同风向影响的速度场空间特征,得到上风向有限差分系数和下风向有限差分系数,将预测得到的有限差分系数同时进入到M3模块,通过风向判断模块给予上下风向系数不同的权重,得到最终受风向影响的空间离散化有限差分系数。下面针对这三个模块进行详细介绍。

1.2 M1及M2部分

本工作结合物理先验知识设计了如图所示的卷积神经网络,M1与M2是完全相同的神经网络,均是由5层卷积层以及1个精度约束层构成。其中网络的输入为Burgers方程的高精度解v,输出为方程中的有限差分系数α。

1.2.1 卷积神经网络 该网络结构主要是在迎风格式的启发下设计的,迎风格式认为在对流项主导的运动里,某个点所受到上游的影响远大于下游所产生的影响。因此对速度值采用了两部分网络进行处理,其中M1作为上风向有限差分系数的预测模块, M2为下风向有限差分系数的预测,对于M1与M2两部分的差分系数将在M3模块进行处理。

1.2.2 卷积神经网络结构 由于M1与M2所设计的网络结构相同,因此本部分只对于M1模块进行详细描述。对于两个分支的卷积神经网络,本工作统一采用的是5层的网络卷积层,内核大小为7×7,有限差分系数使用的网格大小为6,在训练过程中,采用分批训练,批大小为128,模型参数优化的初始学习率设置为10-3,并将Relu作为激活函数进行训练。同时在卷积层之后还加入了精度约束层,主要目的是若差分阶数过低时,通过此约束层使得多项式的精度达到一定的阶数,进一步保证了计算空间导数时的准确性。通过Tensorflow来对神经网络结构进行设计,这样做最主要是因为Tensorflow作为深度学习框架已被广泛应用,并且它有对复杂微分方程的自动微分功能,因此很容易得到计算步骤中所需的方程信息。

1.2.3 M2风向判断模块 本文在以上工作的基础上加入了风向判断模块,对于此模块的设计主要是受到迎风格式思想的启发。下面对此模块的设计细节进行描述,对于一维Burgers方程的解而言,存在着方向的差异性,因此本工作采取了下面的思想进行实验,首先是通过每一时刻所有点的速度方向来确定该时刻整体的风向,该思想主要是通过对每个点周围6个点的速度方向来判断该点的速度方向,若超过1/2的点速度值为正值,则认为该点的速度为上风向,否则为下风向。架构图如图2所示,其中P代表512个网格点,即P={P1,P2,……,P512},C′i代表上风向对于每个网格点所预测的系数,同理,C′j代表下风向对于每个网格点所预测的系数,Ci代表上下风向随预测系数经过风向判断模块后所得到的最终预测系数。对于此模块,风向判断公式如下:

(5)

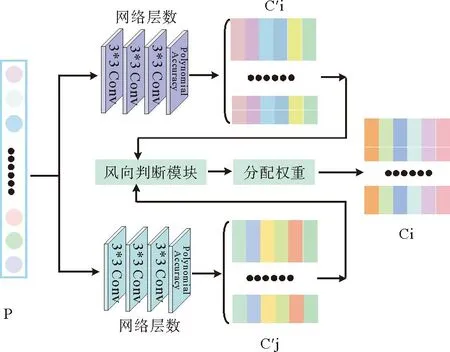
图2 风向判断模块示意图

(6)

式中:N代表风向判断系数;v-代表网格点速度值为负数的情况;num(v-)代表网格点速度值为负数的数量;同理v+代表网格点速度值为正值的情况;num(v+)代表网格点速度值为正数的数量;wu代表上风向差分系数;wd代表下风向差分系数。

若所有点中负速度值的个数不足一半,则认定该时刻的风向为上风向,同时设置风向判断系数为0(如公式(5)所示),在此情况下,给上风向所预测的差分系数(即M1模块)赋予权重为0.9,则下风向预测差分系数值(即M2模块)赋予权重为0.1(如公式(6)所示);同理,若所有点中负速度值的个数超过一半,则认定该时刻的风向为下风向,同时设置风向判断系数为1,在此情况下,给上风向所预测的差分系数(即M1模块)赋予权重为0.1,则下风向预测差分系数值(即M2模块)赋予权重为0.9。

1.3 损失函数及训练工作

为了更好的衡量模型的预测能力,本工作选取MSE损失函数通过利用预测值与真实值之间的差异进行反向传播,然后开展模型训练。公式如下所示:

(7)

2 实验过程及实验结果

为了验证本方法的有效性,该部分将从数据集、训练优化工作以及实验设计等部分验证模型的性能。

2.1 数据集

为了能够生成大量高精度的解,本研究工作选取了五阶WENO方法对Burgers方程进行数值求解,并进行了多次模拟以生成10 000个高分辨率的解,每次模拟均采用了512个网格点,其初始速度场的状态图如图3所示。

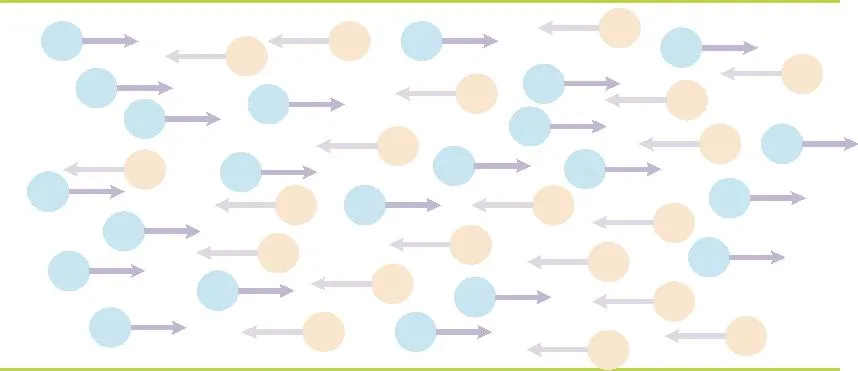
图3 初始速度场状态图

2.2 训练优化方法

为了更好的验证方法的有效性,随机选取了其中的8 000个解作为训练样本,选取2 000个解作为测试样本,通过对神经网络进行了多次模拟,并将最终计算结果与偏微分方程的真实时间倾向项进行比较,此方程的真实时间倾向项,是通过在512个网格点上使用五阶WENO方法计算获得。

为了有效的验证模型的性能,所有工作均通过开源的Tensorflow框架进行模型构建以及完成模型的训练,所有实验均在Tesla V100 SXM2 16 GB GPU上进行的。另外,还选择了由JetBrains打造的Pycharm作为实验开发环境。同时选用Adam优化器对网络进行训练,设置迭代次数(epoch)为40 000,基础批量大小(base_batch_size)为128。在此工作中,采用如下策略进行训练,迭代次数在0～20 000之间时,学习率设置为10-3,当迭代次数在20 000～40 000之间时,学习率设置为10-4,同时每250轮评估一次训练结果。

2.3 评价指标

为了有效的说明工作的有效性,本文选取了Mean Absolute Error(MAE)、Mean_Abs_Relative_Error(MARE)、RMS_Error(RMSE)作为模型性能的评价指标。下面对于每一个指标进行详细说明。

其中MAE为平均绝对误差,其计算公式如下:

(8)

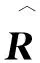
(9)

设计原理同MAE,同样保证了其预测的准确性。RMSE为均方根误差,其计算过程如下:

(10)

同理,RMSE很好的保证了预测结果的精度。

2.4 实验设计

为了能够清晰的表明方法的有效性,设计了一组对比实验以及两组消融实验,分别通过MAE、MARE、RMSE三项指标进行验证。

2.4.1 对比实验和分析 本部分的目标主要是训练神经网络中所需要的参数,所选取的损失函数是经过神经网络预测得到的时间倾向项与传统数值方法所求时间倾向项之间的平均绝对误差,此工作主要是为了优化最后的时导数项,而不是其他项。为了能够充分考虑到方程中的物理信息,在神经网络训练过程中考虑了物理约束对求解精度的影响,从而可以直接对最终的结果进行预测。在该实验中,模型训练大约需要20 min即可完成。在模型训练完成后,对模型进行了测试工作,以检测此模型的预测能力。预测结果如表1所示,其中表中的v代表速度值,v_t代表的是时间倾向项,v_x代表的是空间导数,这充分表明了此方法对于模型的预测能力是可接受的,同时进一步验证了方法的有效性。

表1 对比实验结果表

本文基于五阶WENO方法生成512×512高分辨率网格下高精度解,然后通过降维得到128×128低分辨率网格下高精度解。表1中5th-WENO方法、WENO_NN方法与本工作的误差均代表与上述128×128低分辨率网格下高精度解进行对比的结果。本工作比5th-WENO方法和WENO_NN方法有着更高的精度,从而实现了求解的加速。基线工作在通过神经网络预测差分系数过程中未考虑上下风向对模型预测的影响。通过实验结果表不难发现,该工作明显优于基线方法,这主要是因为该研究方法充分考虑了不同阶段风向对于系数的影响,使得上风向特征信息在系数预测过程中起到关键作用,空间结构信息挖掘更加充分,从而使最终误差减小。

2.4.2 消融实验和分析 此外,本文进行了两组消融实验,第一组实验验证神经网络层数对于模型预测能力的影响;第二组是验证卷积核大小对模型的影响。接下来对这两组实验的实验结果以及实验分析展开描述。

从表2中可以看出当网络层数为5时,模型的预测效果是最好的,这是由于随着网络层数的增加,模型获得的信息越丰富,但是网络层数过多可能会导致信息的冗余,正如网络层为9时的结果。

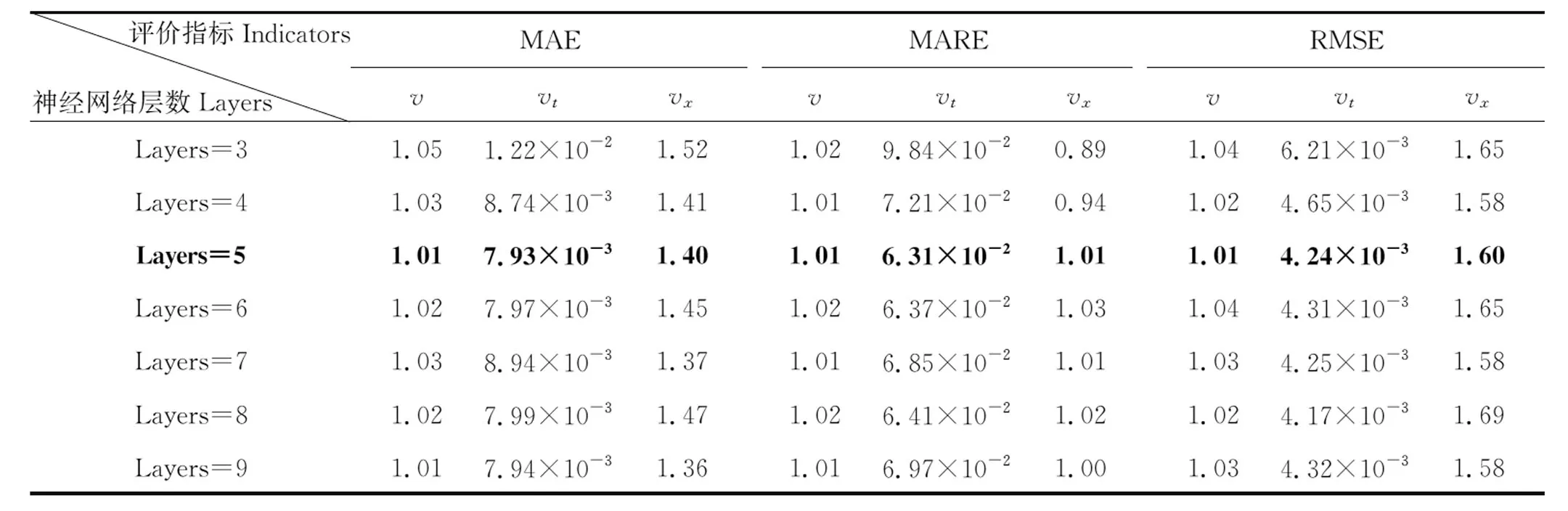
表2 神经网络层数的消融实验

从表3中可以看到,当卷积核大小过小时,会使得卷积核的感受野太小,从而无法有效获取完整的空间信息,进而无法有效提取特征。研究过程所选取的卷积核大小是5,虽然卷积核大小为7时,结果也是可以接受的,但是当卷积核过大时,计算容易出现暴涨现象,计算成本会大幅度增加。

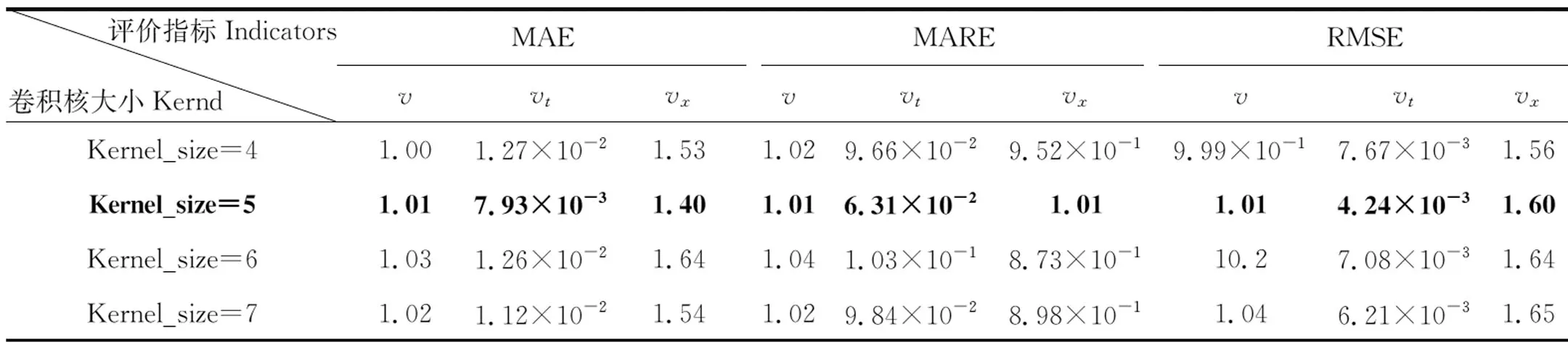
表3 卷积核大小的消融实验

虽然对于方程的计算过程过于复杂,但是本文的工作所得到的结果是满意的,这说明了利用神经网络对方程进行端到端求解是可行的,在提高求解精度的同时,也提高了求解的速度,这个工作思想值得去进一步探索研究。

3 结论与展望

本文介绍了一种使用神经网络与物理信息相结合而进行的数据驱动方法。根据Burgers方程的特点,在原来数据驱动离散化方法基础上做的改进工作,构建了神经网络模型,并对该模型进行了对比实验以及消融实验。由于一维Burgers方程研究工作中受到迎风格式的影响,上风向节点所具有的物理信息在建模过程中占主导地位,同时下风向节点信息也对中心节点有一定的影响,本文经过对比实验以及消融实验得出以下结论与展望:

(1)针对单一建模方式往往难以充分考虑不同阶段风向对系数的影响比重,无法有效获得各节点间关联信息的挑战,研究了迎风格式思想的建模方法,提出并设计了风向监督双流神经网络以及风向判断模块,实现了对预测得到有限差分系数的权重融合。针对此问题,本文提出了风向监督双流神经网络以及风向判断模块,对预测得到的有限差分系数进行合理的权重分配,突出了上风向节点的重要性。通过风向监督双流神经网络,并结合先验知识对学得的系数分配一定的权重,以突出上下风向对预测结果的不同影响,可以有效实现对不同风向上的点分别进行预测,使得空间结构特征信息挖掘更加充分,从而提高差分系数预测的精度。通过与传统数值方法的对比实验可以看出,本工作在MAE、MARE以及RMSE三项指标中均有明显的改善,从而验证了该研究方法充分考虑了不同阶段风向对于系数的影响,使得上风向特征信息在系数预测过程中起到关键作用,空间结构信息挖掘更加充分,从而使最终误差减小。

(2)利用本文的思想对偏微分方程进行求解得到了不错的结果,同时也解决了传统数值求解方法存在计算成本大的问题,这是由于强大的神经网络的模拟能力以及所考虑的物理信息符合Burgers方程所包含的信息所致。在偏微分方程求解的工作中,本文所做的工作将会是一个不错的思路,它将会对偏微分方程的加速求解带来深远的影响,甚至可能会助力该研究领域的发展。

(3)本文所做的工作目前仅在一维情况下进行的实验,但是将本文思想应用于二维甚至更高维的情况下的研究可能会遇到更大的挑战,这也是本研究接下来的重点。此外,在将来的工作中将会更细致的研究偏微分方程的物理信息,尽可能将计算精度与计算效率进一步提升。