三维 Brinkman-Forchheimer 方程解的渐近稳定性

宋雪丽,谢晓甜

(西安科技大学 理学院,西安 710054)

本文研究了如下三维Brinkman-Forchheimer方程全局解的渐近稳定性

(1)

其中Ω表示R3中具有光滑边界的有界开区域,u=(u1,u2,u3)表示流体的速度向量,p表示流体的压力项,f是外力项,ν>0是Brinkman系数,r>0是Darcy系数,b>0,c>0是Forchheimer系数,β>1是一个常数.

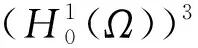
宋雪丽等[10]使用Fourier分解方法研究了当β>10/3时三维全空间上Brinkman-Forchheimer方程弱解的L2衰减性,并讨论了在大初值扰动下弱解的渐近稳定性.MOHAN[11]研究了两时间尺度随机对流Brinkman-Forchheimer方程解的大偏差行为.YU[12]讨论了三维不可压缩对流Brinkman-Forchheimer方程轴对称解的存在及唯一性.

目前,关于流体方程原始方程组解的稳定性研究得到广泛关注.如,文献[13]讨论了三维具有非线性阻尼项的Navier-Stokes方程的解与对应的广义稳态椭圆方程的解之间当t→∞时的收敛性.文献[14]讨论了柱形区域上带震荡随机力的大尺度海洋三维原始方程组的连续依赖性,证明了解对黏性系数的连续依赖性.文献[15]利用微分不等式技巧和能量估计的方法证明了大尺度海洋大气动力学三维黏性原始方程的解连续依赖于边界参数.

由于三维Brinkman-Forchheimer方程与三维具有非线性阻尼项的Navier-Stokes方程(更多Navier-Stokes方程理论可参看文献[16-17])物理背景相似,受文献[13]的启发,本文将研究t→∞时,方程(1)的解与下述广义稳态椭圆方程的解之间的关系.

(2)

其中f∞与t无关,可以看作时间t趋于无穷时f(x,t)的极限.同时,受文献[14-15]的启发,也将讨论方程(1)的解关于初值及Brinkman系数ν的连续依赖性.

1 预备知识

在本节中,主要对接下来要用到的符号及函数空间做一简单说明.

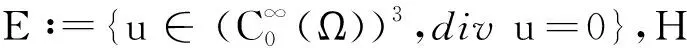
H和V是可分的Hibert空间,H=H′,H′是H的对偶空间,V′是V的对偶空间.‖·‖和〈·,·〉分别表示V′中的范数和对偶积.字母C是正常数,在不同行,甚至在同一行可能表示不同的值.

2 方程(1)与方程(2)的解之间的收敛性

2.1 方程(2)平稳解的存在唯一性

定义1设f∞∈V′,若u*∈V∩Lβ+1(Ω)满足νa(u*,υ)+r(u*,υ)+b(|u*|u*,υ)+c(|u*|β-1u*,υ)=〈f∞,υ〉,对于所有的υ∈V∩Lβ+1(Ω),则称函数对(u*(x),p*(x))是方程(2)的一个弱解.此外,若弱解u*满足u*∈D(A),称(u*,p*)为方程(2)的一个强解.

定理1考虑广义的稳态椭圆方程(2),有

(i)对于所有的f∞∈V′,β≥1,方程(2)存在一个弱解(u*,p*);

(ii)如果f∞∈L2(Ω),β≥1,那么(u*,p*)是一个强解;

(iii)方程(2)有唯一弱解.

(3)

下面应用Brouwer固定点定理(文献[18]中定理4.3)来证明式(3)存在一个解.

设ξ={ξ},对于1≤i≤m,记

(4)

记P(ξ)=∶η={ηi},可以得到

(5)

容易验证对充分大的ρ,

(P(ξ),ξ)≥0,在|ξ|=ρ上,

(6)

(7)

这意味着

(8)

这里C是一个常数与m无关.

(9)

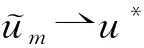
(10)

(11)

(12)

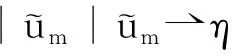
(13)

(14)

当m→+∞时,有u*∈V∩Lβ+1∩L3.

应用文献[18]中的引理1.3并且结合式(9)、(13)和(14),能得到ζ=|u*|β-1u*,η=|u*|u*.因此,对式(3)两端取极限,得到u*是方程(2)的一个弱解.

(15)

(16)

通过简单计算,有

(17)

故

(18)

因此

(19)

故u*∈D(A)是方程(2)的强解.

(iii)设u1和u2是方程(2)的两个弱解,有

νa(u1-u2,υ)+r(u1-u2,υ)+b(|u1|u1-|u2|u2,υ)+c(|u1|β-1u1-|u2|β-1u2,υ)=0.

(20)

对∀υ∈V∩Lβ+1(Ω).取υ=u1-u2,有

(21)

2.2 方程(1)与方程(2)弱解之间的指数收敛性

定理2对于任意的T>0,β≥1,假设初值u0∈H,f∈L2(0,+∞;V′),且存在f∞∈V′,使得对于足够小的μ>0,有

(22)

(23)

假设u(x,t)是方程(1)的弱解在下文用u(t)表示,初值为u0,外力项为f,u∞是方程(2)对于外力项为f∞的唯一弱解.则存在两个足够小的正常数C和λ(C仅依赖于ν,λ仅依赖于λ1,ν和μ)使得

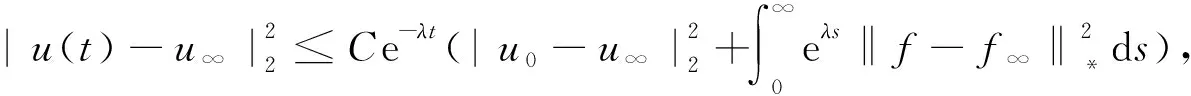
(24)

证明记ω=u(t)-u∞,易得:

c(|u|β-1u-|u∞|β-1u∞,ω)=〈f-f∞,ω〉.

(25)

由式(25)可得:

(26)

对于任意固定的λ>0,

(27)

应用Poincaré不等式,有

(28)

对于任意的0<λ<λ1ν对式(28)关于时间变量t进行积分,得到:

(29)

对于足够小的0<λ<λ1ν,限制λ<μ,得到:

(30)

两边同时除以eλt,得到:

(31)

定理得证.

3 方程(1)强解对初值及系数的连续依赖性

假设u和υ是方程(1)的解,满足:

令ϖ=u-υ,α=ν1-ν2则ϖ满足下面的初边值问题:

(32)

从文献[9]中知道当方程(1)的初值在V中取值时,方程强解在H,V,Lβ+1(Ω)及(H2(Ω))3中均存在有界吸收集,这里1<β<5.为了下面讨论方便,假设强解在(H2(Ω))3中的有界吸收集为B.由于VH,Lβ+1(Ω)V,(H2(Ω))3V,因此B也是强解在H,V和Lβ+1(Ω)中的有界吸收集.故对∀u0∈B,|u(t)|2≤A1,|u(t)|2≤A2,|u(t)|β+1≤A3,|Δu(t)|2≤A4,A1,A2,A3,A4均为正常数.

定理3设初值u0,υ0∈B,1<β<5,则问题(32)的解满足下面不等式:

对上述不等式应用Gronwall不等式,有:

因此,当u0→υ0,ν1→ν2时u→υ在H中.

证明将式(32)的第1式两端与-Δϖ做内积,得到:

(c|u|β-1u-c|υ|β-1υ,-Δϖ)-α(Δυ,Δϖ).

(33)

现在对式(33)的右端逐项进行估计.用到如下Sobolev不等式:

|u|p≤d0|u|2,1≤p≤6,∀u∈V.

(34)

(35)

(36)

(37)

(38)