善于观察探思路——以中考平面几何题为例

夏 佳

(江苏省扬州市扬州大学,江苏 扬州 225100)

波利亚在《怎样解题》中将解题步骤分解为“理解题目——拟定方案——执行方案——回顾”.然而,这并不能使每个解题者都能按部就班地解题,有些学生在解题时如无头苍蝇在迷宫中乱撞,浪费了大量时间在试错上却不能将问题解决.从心理学视角来看,问题解决过程中,与新手相比,专家们会将更多时间放在表征问题上,能很快抓住问题的实质,并根据问题的内在结构表征问题.

1 概念界定

观察是一种人类对周围出现的事物或现象进行有目的的考察所表现出来的心理现象,先进行全面而深入的察看,并根据该事物或现象的真实面貌来探究和确定它们的性质和关系[1].而在数学教学活动中的观察,则是指观察由符号、字母、数字或文字所表示的数学关系式、命题、问题及图表、图象、几何图形的结构特点.

2 善于观察探思路

郑步春认为观察能力的特点为目的性、有序性、取舍性、敏锐性、全面性[2].虽然夏宛央在其学位论文中批判了对观察能力特点的分类,指出这些分类不为“观察能力”所特有,因此也就不能表明“观察能力”的质[3].其目的性在于它是指向问题解决的,目的是为了探求解题思路;其有序性在于观察需遵循整体到局部再到整体的顺序;其取舍性在于需对观察到的信息进行取舍,直指问题的本质特征;其敏锐性在于需要注意到易于忽略的信息;其全面性在于需通过观察关注到问题的显性信息和隐形信息.从这些特性也就能得出在数学活动中应如何观察探思路,即带着目的,从问题整体出发,留意问题的已知数据、条件和未知量,找出问题的显性信息和隐形信息,再对局部仔细琢磨推敲,观察不同部分,从不同角度思考同一部分,最终探明从已知数据到未知量的路径,得到解题思路.

3 案例分析

笔者以两道中考题为例,说明如何通过观察题干、已知量与未知量的联系得出问题的求解方法.

例1 (2021年重庆市中考数学B卷第26题)在等边△ABC中,AB=6,BD⊥AC,垂足为D,点E为AB边上一点,点F为直线BD上一点,连接EF.将线段EF绕点E逆时针旋转60°得到线段EG,连接FG.

(1)如图1,当点E与点B重合,且GF的延长线过点C时,连接DG,求线段DG的长;

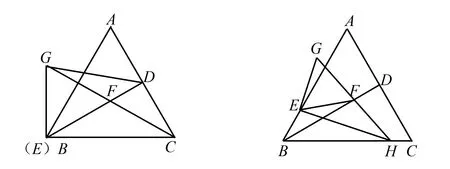
图1 问题(1)图

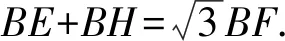
针对问题(1),观察题干:

已知量:△ABC为等边三角形,AB=BC=AC=6,三内角均为60°;由BD⊥AC,垂足为D,易得∠ABD=∠CBD=30°,AD=CD=3;由EF=EG,∠GEF=60°,得△EFG为等边三角形,∠CBG=90°.

未知量:DG的长,易发现DG在△DFG、△CDG、△DEG中,连接AG,则DG还在△ADG中.

观察已知量与未知量的联系:

思路1:△CDG中已知CD,要求DG,需先求出CG长与∠ACG,由隐含信息可求得,继而求DG长.

思路2:△ADG中已知AD,要求DG,需先求出AG长与∠DAG,由隐含信息可求得,继而求DG长.

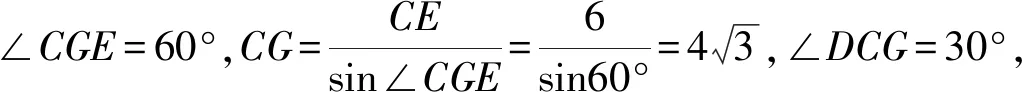
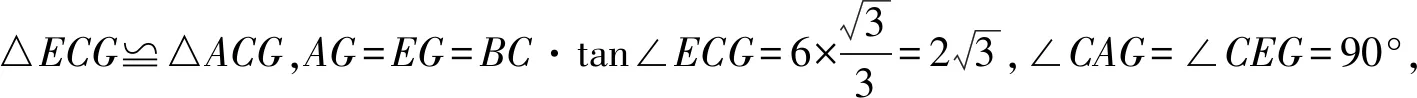
观察题设:先找出隐含信息,△EFG为等边三角形,得出∠EFH=120°,又∠ABC=60°,易发现∠BEF=∠CHF,BE与BF同在△BEF中,HC与BH共线,且∠BEF=∠CHF,不妨作直线FP=FB且与BH所在直线相交,容易得到两三角形全等,BE=HP,达到使与BE、BH长度相等的线段共线目的,这时就可顺理成章地获得.

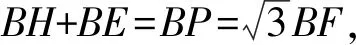
图3 问题(2)求解图

(1)如图4,EF与AC交于点G,连接NG,求线段NG的长;

图4 问题(1)图

(2)如图5,将△AEF绕点A逆时针旋转,旋转角为α,M为线段EF的中点,连接DN,MN.当30°<α<120°时,猜想∠DNM的大小是否为定值,并证明你的结论.

对于问题(2),观察整体:题干中提到许多中点,如D、M、N分别为BC、EF、EC中点.题中要求猜想∠DNM的大小是否为定值,并证明结论,观察题目可知为定值的角有∠ABC=∠BAC=∠ACB=60°,∠EAF=∠AEF=∠AFE=60°.

观察局部:已知量为点D、M、N分别为BC、EF、EC中点,在图中更直观地可以看到DN、MN,从而联想到三角形的中位线定理,不妨连接BE、CF,再有△ABC、△AEF都为等边三角形,不难发现∠BAE=∠CAF,从而得出△ABE≌△ACF.未知量为∠DNM,若想得出∠DNM大小,不妨尝试延长FE与DN相交,但显然此路不通,只能从其他方面入手.

观察已知量与未知量的联系:∠DNM为定值,已知量中为定值的角有∠ABC=∠BAC=∠ACB=60°,∠EAF=∠AEF=∠AFE=60°,试图将∠DNM与这些角联系在一起,∠DNM不可直接求得,可将其转化成求其他角的大小.

解如图6,连接BE,CF.因为AB=AC,AE=AF,∠BAE=∠CAF,所以△ABE≌△ACF,所以∠ABE=∠ACF.因为∠ABC+∠ACB=60°+60°=120°,所以∠EBC+∠BCF=∠ABC-∠ABE+∠ACB+∠ACF=120°.易得∠ENM=∠ECM,∠CDN=∠EBC.因为∠END=∠NDC+∠ACB,从而易知∠DNM=∠DNE+∠ENM=∠NDC+∠ACN+∠ECM=∠EBC+∠ACB+∠ACF=∠EBC+∠BCF=120°.

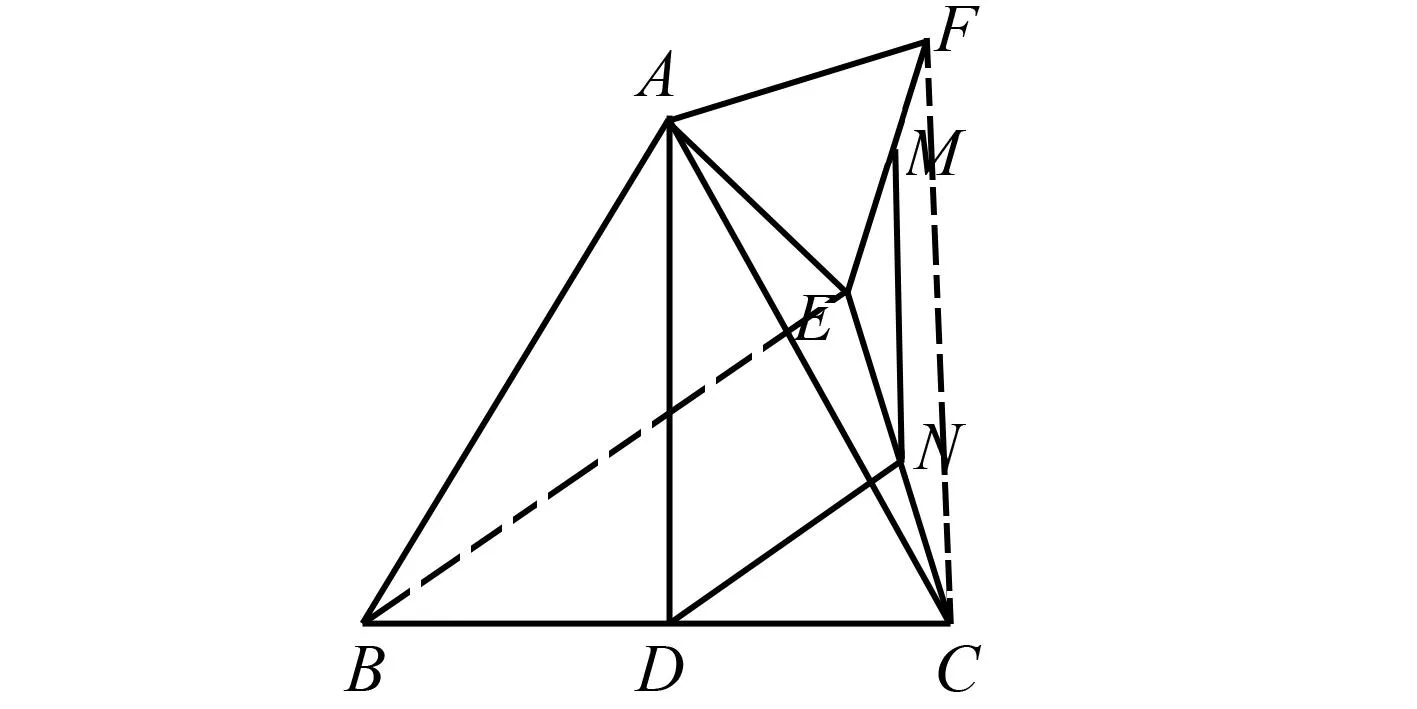
图6 问题(2)求解图

4 观察方法总结

4.1 注意观察整体

观察整体的目的是对问题有一个整体的印象,抓住问题的主要特征.如例2(2),通过观察整体,发现题中有多个角均为定值,要想求得未知量,就要将其与其他定值角联系在一起.若未先观察整体,而先从部分入手,很可能只能获得一些无效信息,解题解到中途发现前面都是在做无用功.

4.2 观察已知量(题设)与未知量(结论)的联系

不论是求解题还是证明题,问题解决的途径就是探明已知量到未知量、题设到结论的路径,因此观察已知量(题设)和未知量(结论)之间的联系显得尤为重要,一种方法是从已知量顺推至未知量.

4.3 观察得到问题中的隐含信息

问题解决过程中往往很难一眼就看出从已知量到未知量的路径,经常需要找到题中的隐含信息,并借助其作为台阶一步一步从已知量走向未知量.当然,并不是盲目地探寻隐含信息,而是要带着问题解决的目的去寻找,还要注意甄别隐含信息中哪些信息是有效信息,哪些信息是无效信息,为问题解决创造条件.

4.4 观察过程中注重联想,大胆试错

联想能力和观察能力一样,都是问题解决过程中不可或缺的思维能力.此外,通过观察、联想,还要大胆试错,因为有时解题思路并不明了,找到一个突破口之后,便要勇于尝试,看能否向下一步推进.这是问题解决过程中解题者需要调动的非认知能力,有的解题者不敢轻易试错,生怕踏错一步,于是便只能踌躇不前.

5 结束语

通过观察、解读题目,找出已知数据和未知量的联系,探求解题路径,在脑海中构思解题思路,是解题过程极重要的环节,而解题困难者则缺失了这一环.在这重要一环中,观察便是解题者需要调动的一种重要的思维能力,因此,教师在平时的教学中应注重培养学生的观察力.