平面应变模具尺寸差对金属流变及其力能的影响
潘红波,唐 荻,胡水平,王潇潇
(北京科技大学高效轧制国家工程研究中心,北京100083)
平面应变模具尺寸差对金属流变及其力能的影响
潘红波,唐 荻,胡水平,王潇潇
(北京科技大学高效轧制国家工程研究中心,北京100083)
采用MARC/Superform有限元软件对平面应变压缩过程进行了二维有限元分析,分析了上下模具尺寸不相等时,对金属流变规律及其力能参数的影响.同时应用滑移线场理论对端部的滑移线场进行了分析,分析了金属的流动情况,进一步验证了有限元模拟结果的可靠性.研究结果显示:模具尺寸相等时,金属流动呈现对称分布;当上下两个模具尺寸不等时,金属流动呈现非对称分布,有剪切变形产生.而且随着模具尺寸差的增大,其交叉剪切变形越严重,总压力也增大,平均压力相对降低,这与异步轧制过程类似.所研究结果为异步轧制过程提供了一种新的物理模拟方法.
平面应变压缩;金属流变规律;滑移线场;非对称流动;异步轧制
由于平面应变技术与板带钢轧制技术的变形条件、边界条件等都一致[1](如图1a所示),因此广泛用来模拟热轧板带条件下金属变形、晶粒长大、变形带、亚晶的形成以及变形织构的进展等[2~3].同时由于在平面应变过程中变形比较均匀,因此在变形抗力(金属变形流动应力)以及轧制力模拟方面也得到了广泛的应用[2,4].而且相对于拉伸以及轴对称压缩而言,平面应变技术的应变量大、变形均匀、变形试样的尺寸大,而且还能研究材料变形过程中的组织变化规律等优点[5,6].但是由于平面应变技术要求相当严格,对试样尺寸、模具尺寸、对称性、摩擦都有严格的要求,大大限制了其应用范围[7].然而研究平面应变技术各影响因素对金属流变特性及力能参数的规律,以拓宽平面应变技术理论的发展鲜有报道.
异步轧制具有轧制压力小,产品精度高,特别适合于轧制薄带和超薄带[8].变形后有利于退火过程中形成强烈的立方织构,因此在高压电容器高纯铝箔生产中具有很大的潜力[9,10].由于其轧制板带薄、精度高,而且变形后有利于硅钢退火过程中,在三次再结晶过程中形成强烈的高斯织构,因此在取向硅钢方面获得了很广泛的应用[11].同时由于异步轧制在变形区中形成“搓轧区”,从而使变形金属发生强烈的剪切变形,对一些塑性不好的金属(如密排六方金属)可以进行大变形而不产生裂纹.采用异步轧制时,由于搓轧区强烈的剪切变形作用,从而改善了变形条件,使柱面滑移系也参与滑移,产生多系滑移与交滑移现象,有利于变形量的增大,使基面织构与孪晶大为减少.当变形量很大时,将不产生孪晶,而为等轴晶粒,晶粒细小,从而有利于进一步后续变形[12,13].
目前实验室对异步轧制过程的模拟均在试验轧机上进行,温度很难控制,而且很多实验室的轧机为同轴传动,因此需要做很大改动,投资费用大.由于异步轧制过程的几何条件、边界条件等与模具尺寸有一定差值的非对称平面应变压缩一致(如图1b所示),但是对此方面的研究与应用国内外还未见报道.因此本工作对模具尺寸不同的平面应变流变特性以及力能参数进行分析,为异步轧制过程物理模拟提供理论基础,对异步轧制过程的物理模拟提供新的切实可行的方法.
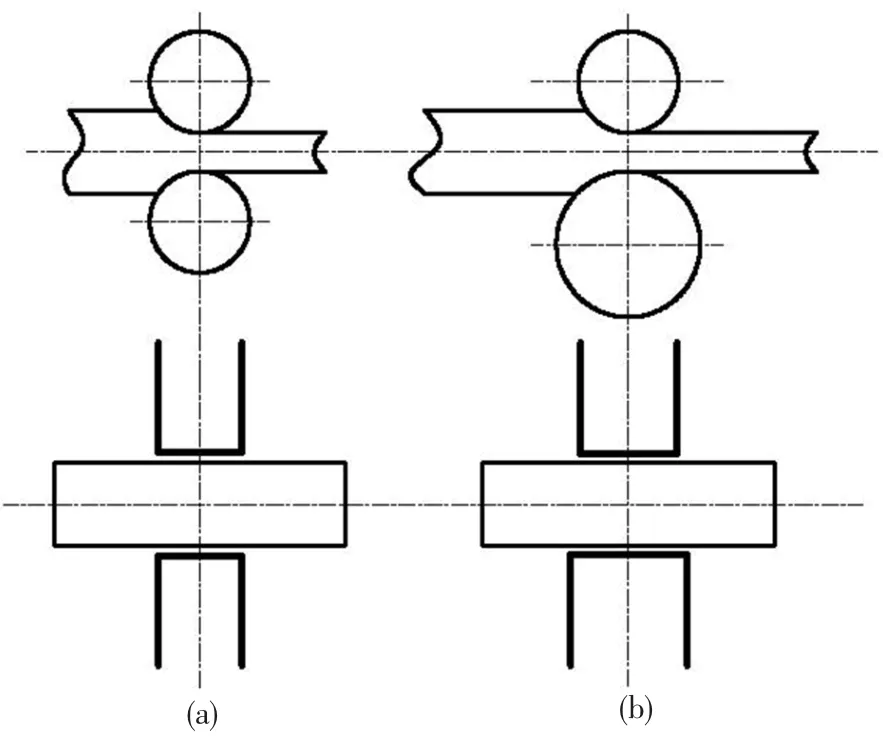
图1 轧制过程与对应的平面应变压缩过程示意图
1 试验方案
本文采用数值模拟及理论分析相结合的手段,对平面应变过程中上下模具尺寸差对应变场和金属流动、力能情况进行了研究分析.在研究过程中,采用不同模具尺寸差别,研究其差值对应变场、金属流动状况以及力能的变化.由于本研究是为随后的大试样平面应变热模拟试验机提供理论基础的,因此模具尺寸较宽,以便试验后的试样能对其进行圆棒拉伸以及冲击等力学性能试验.在数值模拟过程中上模尺寸保持不变,恒为30mm.根据下模尺寸的变化,对其结果进行比较分析,同时结合异步轧制流变状况,对其金属流动及力能参数进行分析.最后,采用滑移线场理论对其端部滑移线场进行分析,来进一步证实金属流变状态.
2 有限元模型及其结果分析
2.1 有限元模型及其边界条件
在数值模拟方面,利用具有强大非线性大变形能力的MSC/Superform有限元软件,由于主要是研究应变分布及其金属流变状态,在模拟过程中忽略热传导以及对流等传热过程,只对其进行力分析.由于其对称性,以及减少运行时间,故对其只进行二维力分析.研究不同模具尺寸差(= 0,10mm,20mm,30mm)对应变分布及流变状态的影响,其有限元模型如图2所示.

图2 不同模具尺寸差有限元模型
模拟坯料尺寸为40×60 mm,将坯料从原始40 mm变形到10 mm.将原始坯料进行网格划分,其划分结果如图2所示.由于变形比较大,在计算过程中,对网格参数进行设置,采用网格重划分.在变形过程中,初始条件为温度恒定,其值为1000℃.试验材料的物理特性由软件直接提供,直接从其材料库中读取,其材料为C60.在建模过程中,忽略模具的弹性变形等微量变形,将上下模具均设置为刚体,只考虑材料的变形过程,模具与变形体接触面间遵循库仑摩擦,它们之间的摩擦系数取为0.1.在处理过程中,下模固定不动,上模运动;在工况选择过程中,选择“液压冲击”对其进行分析,在时间与步长方面,采用自适应的方式.
2.2 有限元结果与分析
2.2.1 应变场与金属流动分析
上下模具尺寸差别对金属的流动以及应变分布的影响是显著的.图3为不同不同尺寸差值下,试样变形后的形状和等效应变分布等值带的情况.可以看出,当上下模具尺寸相等时,也即= 0mm情况下,金属流动、试样尺寸、应变分布均是对称的,如图3(a)所示.当上下模具尺寸不等时,也即存在一个差值时,金属流动、试样尺寸、应变分布将呈现出不对称分布,如图3(b)(c)(d)所示,而且随着值的增大,其非对称性越来越严重.其等效应变等值带呈现出“V”字型,其等效应变将向模具尺寸较小的一侧发生弯曲,呈现出强烈的剪切变形状态.而且随着值的增大,其“V”字型分布越来越严重.同时,从图3中的尺寸标注可得出,随着值的增大,模具较小侧的深度越大,模具较大侧的深度越小,也即金属偏向模具较小一侧流动.当下模尺寸达到60mm,也即=30mm时,下模一侧的金属几乎没有发生变形,而完全由上模对试样进行冲压.结合轧制过程,当=0mm时,其金属流动、应变分布与常规轧制过程一致;当在零到小模具尺寸变化时,其金属流动、应变分布与异步轧制过程一致,可以结合试样尺寸与模具尺寸差,即可模拟异步轧制过程不同速比情况.当大于等于小模具尺寸时,靠近下模侧金属将不发生变形,而完全是小模具对试样进行冲压的过程.

图3 变形体总的等效应变分布及其几何形状

图4 Δ=0时等效应变与金属流动随时间步的变化分布

图5 Δ=10mm时等效应变与金属流动随时间步的变化分布
发生上述现象并不是变形开始就产生的,而是与试样厚度、模具尺寸差有着很大的关系.图4、图5、图6分别为=0、10 mm、20 mm情况下随变形深入的应变分布示意图.从图4看出,当=0时,在整个变形过程中,金属流动、应变分布始终呈现对称分布;当=10 mm时,也即图5所示,变形开始阶段,金属的流动状态、应变分布开始均匀的,到60步长时,还保持着对称形状;当进行到一定程度之后,也即达到94步之后,等效应变开始呈现出“V”字型,而且随着变形的继续深入,其“V”字型越来越严重.当=20mm时,只有刚开始一小段时间内,金属流动与应变保持对称分布,到60步之后,等效应变就开始出现非对称分布,当进行到96步时,其等效应变就呈现呈强烈的“V”字型.也即随着值的增加,其等效应变呈现“V”字型越厉害,而且开始呈现“V”字型所需的变形越小,也即越容易发生“V”字型分布.这种情形与轧制过程也一致,常规轧制的金属流动与应变分布在整个过程中始终是对称的,与对称平面应变过程的情形一致.而异步轧制,随着速比的增加,金属流动与应变分布呈现非对称的时间越早,最后剪切变形越严重,这与有一值平面应变过程时是一致的,也即可以采用不同值,就可以模拟异步轧制情况下,不同速比的物理模拟过程.
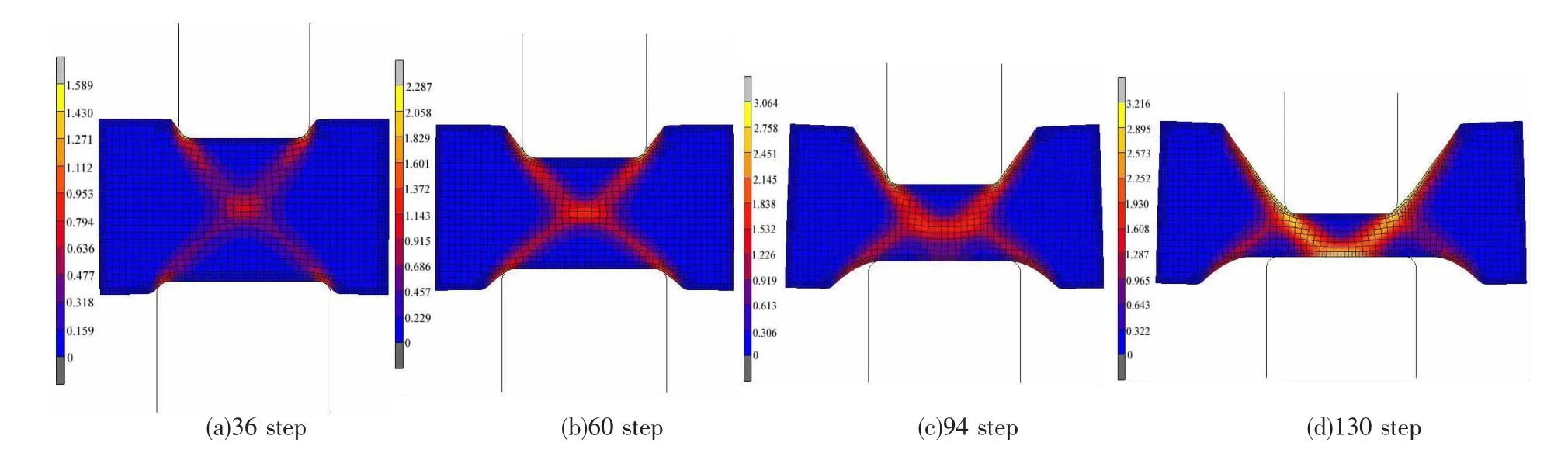
图6 Δ=20mm时等效应变与金属流动随时间步的变化分布
2.2.2 力能分析
不同值下,其压力曲线如图7所示.从图可看出,随着值的增加,也即随着下模尺寸的增大,其总压力也相应增大.这是因为随着值的增大,试样将发生剪切变形,而且试样越容易偏向小模具一侧流动,从而使金属的流动路径增大,阻力也相应增大,因此表现在压力曲线上,就是如图7所示情形.同时从图可看出,=0与=10mm时,其压力差别很小,当值增大时,其差别更加显著.这是由于金属流动形成加长、剪切作用加强的缘故.当= 30mm,也即小模具尺寸时,其压力异常增大,其值是=0时的4倍左右,这是因为此时金属在下模具侧不发生流动,而呈现出纯冲击过程,将导致试样的应力状态发生明显的变化,从而表现在压力上,呈现出异常增大的现象.因此,在采用不同模具尺寸差来模拟异步轧制过程时,要注意上下模具之间的差值大小.在0≪30mm范围内,虽然总压力随着值的增大而增大,但是表现在下模具(即宽模具)上的单位压力比对称模具尺寸单位压力小,即总压力的增大没有模具增大速度快,这一点与异步轧制过程较常规轧制过程压力小的结论是一致的;这进一步证实了用不同模具尺寸差值来模拟异步轧制过程是可行的.
3 理论分析
为了对不同模具尺寸差值的金属流动情况进行理论分析,在此采用上下模具尺寸相等以及上下模具尺寸之间有一定差值进行滑移线场分析,以分析前面所产生的金属流动原因.在平面应变情况下,最简单的滑移线为模具尺寸相等、严格对中且光滑情况下,其滑移线场与平砧压缩薄件类似,此时端部的滑移线场为与模子水平面成45°,且相交于试样中心线的一簇等腰直角三角形组成.为了分析模具尺寸差值的影响,在此将别的情况都简化为最简单的情况.图8为Δ=0与Δ≠0两种情况下试样边界处的滑移线.当Δ=0时,其滑移线场为关于试样中心以及模子中心呈现对称分布,刚塑性出口边界为关于试样中心以及垂直轴线对称分布的流动模式,在上模具侧与下模具侧的滑移线场是一致的.当Δ≠0时,其滑移线场是不对称的,而且与模具水平截面的夹角也不成45°,在宽模具侧(本研究中为下模具),其夹角小于45°;而在窄模具侧(本研究中为上模),其夹角大于45°.从而导致向上模具方向流动的金属比例大于向下模具方向流动的金属比例,而且随着值的增大,其比例差值越来越大[3].这证实了图3中的数值模拟结果.当值与大于等于试样厚度的2倍时,其端部滑移线将起源于窄模具(本研究中为上模具)端部,垂直于宽模具(本研究中为下模具),此时Φ=0,也即此时金属将完全向窄模具方向流动,也即此时的变形相当于在一个厚厚的试样中冲出一定大小尺寸孔洞过程.
将试样作为参照物,假设试样是不动的,在变形过程中,上下模具相对其作相对运动,并且上模具的相对运动速度为VA,下模具的相对运动速度为VB.由上面的分析可得出,当Δ=0时,试样的滑移线场是对称的,也即变形金属向两个模具侧流动的比例是一致的,此时VA=VB;当≠0时,根据其滑移线场可知,流向上模具金属的比例大于流向下模具金属的比例,表现在模具速度上,即为VA〉VB;当偏移量大于或者等于试样厚度的两倍时,宽压头的速率VBΔ将为0,而且下凹变形也停止进行[3].此情况与异步轧制过程时相反,但是其流变规律、剪切变形等均与异步轧制过程一致,因此出现此情况并不影响其模拟异步轧制过程.

图7 不同模具尺寸差值情况下压力曲线
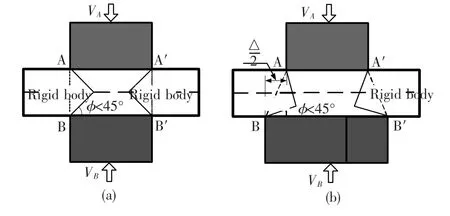
图8 Δ=0与≠0两种变形情况下刚塑性出口边界的滑移线示意图
4 结论
(1)平面应变过程中,上下模具尺寸差的大小对金属流变、应变分布有很大的影响,而且存在着强烈的剪切应变.当=0时,其流变规律与应变分布将呈现对称分布;当≠0时,将呈现非对称分布,而且随着值的增大而增大,其剪切变形的作用也将增大.在较小的值下,刚开始变形过程还是对称的,随着变形的深入,将呈现出非对称分布状态;在较大的值下,在刚开始的变形阶段就会产生非对称分布,完全为剪切变形作用.
(2)随着模具尺寸差值的增大,其总压力相对增大.在较小的值下,其总压力增加值很小,分布在宽模具上的单位压力相反减小;当值增大一定值后,其压力将异常增大,此时为完全剪切变形作用,改变了变形体的应力状态,使其压力增大.
(3)由于不等模具尺寸平面应变的金属流变状态、应变分布等规律与异步轧制过程一致,因此可以根据异步轧制速比、试样厚度的不同,选择不同的模具尺寸差,即可模拟异步轧制过程中金属的流变情况、材料组织与织构在变形过程中的进展规律等.为异步轧制过程开辟了新的物理模拟方法,也拓宽了平面应变理论的应用范围.
[1]牛济泰.材料和热加工领域的物理模拟技术[M].北京:国防工业出版社,1999.
[2]HAND R J,FOSTER S R,SELLERS C M.Temperature changes during hot plane strain compression testing[J].Materials Science and Technology,2000,16(4):442-450.
[3]GLEZ J Ch,DRIVER J H.Substructure development in hot plane strain compressed Al-1%Mn crystals[J].Acta Materialia,2003,51(10~11):2989-3003.
[4]SILK N J,VAN M R.der Winden.Interpretation of hot plane strain compression testing of aluminium specimens[J].Materials Science and Technology,1999,15(3): 295-300.
[5]MIRZA M S,SELLARS C M.Modelling the hot plane strain compression test Part 2-Effect of friction and specimen geometry on spread[J].Materials Science and Technology,2001,17(9):1142-1148.
[6]WONG S F,HODGSON P D,THOMSON P F.Comparison of torsion and plane-strain compression for predicting mean yield strength in single-and multiple-pass flat rolling using lead to model hot steel[J].Journal of Materials Processing Technology,1995,53(3-4):601 -616.
[7]刘雅政,任学平,王自东,等.材料成形理论基础[M].北京:国防工业出版社,2004.
[8]朱 泉.异步轧制实验研究[J].钢铁,1980,15(6):1-6.
[9]吕爱强,蒋奇武,王福,等.异步轧制对高纯铝箔冷轧织构的影响[J].金属学报,2002,38(9):974-978.
[10]黄涛,曲家慧,胡卓超,等.高纯铝箔在异步轧制和再结晶过程中取向的演变[J].金属学报,2005,41 (9):935-957.
[11]高秀华,齐克敏,邱春林.硅钢极薄带三次再结晶退火过程中的组织演化[J].材料热处理学报.2006,27(4):92-95.
[12]Su-Hyeon Kim,Bong-Sim You,Chang Dong Yim.Texture and microstructure changes in asymmetrically hot rolled AZ31 magnesium alloy sheets[J].Materials Letters,2005,59(29~30):3876-3880.
[13]张文玉,刘先兰,陈振华,等.异步轧制对AZ31镁合金板材组织和性能的影响[J].武汉理工大学学报.2007,29(11):57-61.
Effect of die geometry on metallic rheology and pressure during plane strain compression
PAN Hong-bo,TANG Di,HU Shui-ping,WANG Xiao-xiao
(National Engineering Research Center for Advanced Rolling Technology,University of Science and Technology Beijing,Beijing 100083,China)
With the aid of FE code MARC/Superform,2-D mechanical analyses of different die size during plane strain compression were conducted and metallic rheology,force and energy parameters in the process of deformation were analyzed.The slip line field of the ends was analyzed by using theory of slip line field,the flowage of metal was analyzed,and the result of simulation was further verified.It is shown that the flow pattern of metal is symmetrical when the sizes of upper die and down die are identical,however,the flow pattern of metal is asymmetrical and cross shear deformation is arised when the sizes of upper die and down die are different.With the increment of size difference between upper die and down die,cross shear deformation becomes more serious and total pressure becomes greater,but average pressure decreases.These conclusions are identical with those of cross shear rolling.The research provide for a new physical simulation method cross shear rolling.
plane strain compression;metallic rheology;slip line field;asymmetric flow;cross shear rolling
TG335.1文献标识码:A文章编号:1005-0299(2010)02-0284-05
2008-06-13.
教育部211工程重点资助项目“物理模拟系统——大试样平面应变热模拟试验机的研究“.
潘红波(1978—),男,博士研究.
(编辑 张积宾)

