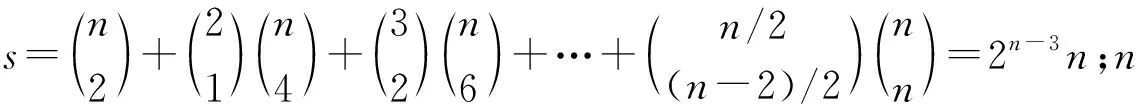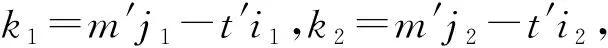关于切比雪夫型方程组的研究
黎海燕,吴 康
(华南师范大学数学科学学院, 广东广州 510631)
以俄国著名数学家切比雪夫(Tschebyscheff,又译契贝雪夫等,1821—1894)的名字命名的重要的特殊函数,第一类和第二类切比雪夫多项式Tn(x)和Un(x),源于多倍角的余弦函数和正弦函数的展开式.
目前对切比雪夫多项式构成的方程组(也称为切比雪夫型方程组)有了初步的研究成果[1-2],更为一般的切比雪夫型方程组的解,目前尚未见有报道.本文主要讨论2类二维切比雪夫型方程组的解.
1 预备知识
定义1[3]第一类切比雪夫多项式定义为:
Tn(x)=cos(narccosx)=

定义2 第I类二维切比雪夫型方程组定义为:
(1)

定义3 第II类二维切比雪夫型方程组定义为:
(2)

引理1[4]设f(x,y),g(x,y)是2个复系数的二元多项式,
f(x,y)=a0(y)xn+a1(y)xn-1+…+an(y),
g(x,y)=b0(y)xm+b1(y)xm-1+…+bm(y),
其中ai(y)(i=0,1,…,n)和bj(y)(j=0,1,…,m)是y的多项式.R(f,g)为f(x,y)与g(x,y)的结式[3].如果(x0,y0)是方程组
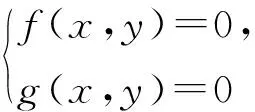
(3)
的一个复数解,那么y0就是R(f,g)=0的一个根;反过来,如果y0是R(f,g)=0的一个复根,那么a0(y0)=b0(y0)=0,或者存在一个复数x0,使(x0,y0)是方程组(3)的一个解.
为了求解方程组(3),先求高次方程R(f,g)=0的全部根,再把R(f,g)=0的每个根代入方程组(3),再求x的值.从而得到方程组(3)的全部解.


(aj-i)t=k-j.
(4)
当i=aj且k=j时,对任意t,都有式(4)成立.所以,对于任意t,当j=j0时,有k=j0.
2 结果

(cos(-mk1δ+jπ),cos 2k1δ)
及 (cos(-mk2φ+jπ),cos 2k2φ),

(cospk1δ,cosk1δ),(cos(π-pk1δ),cosk1δ)
(k1=0,1,2,…,p2-1),
(cospk2φ,cosk2φ), (cos(π-pk2φ),cosk2φ)
(k2=1,2,…,p2),
其中,δ=π/(p2-1),φ=π/(p2+1).
定理2 若切比雪夫型方程组(1)有解,则其全体复数解中,相异解的个数至多为m2个.

定理3 若切比雪夫型方程组(2)有解,其中t≥2,则当2t>m时,方程组(2)有2t个复数解;当2t 注2 由于m<2t时,方程组(2)的全体复数解类似m>2t时讨论可得,往下只讨论m>2t的情形. 定理4 当t≥2,m>2t时,方程组(2)的全体复数解有m个,解通式为 (cos(k1δ+2jk1π)/t,cosk1δ), j=f(k)= 其中〈a1,a2,…,at〉为J的一个排列,且有以下结论成立. 结论3 若m≡(modt),当j=j0时,若k属于k0类,则k0满足j0′≡k0(modt′),其中,′=/d. 总结第II类二维切比雪夫型方程组全体复数解的求解步骤如下: (1)求出如定理4所述的解的通式及相应j,k的可取数集J,K. (2)根据j0′≡k0(modt′),求出j所对应的k0,用结论3所示的方法对j进行分类(求解过程中,只要求得每一类的一个j值,则可根据结论1所示j的等差性求出该类的所有j值). 解得: (5) (6) (7) (8) 解(αn,βn) (n=1,2,3,4)分别为 (mβ1/2+j1π,2(2i1-mj1)π/(m2-4)), (mk1δ+j1π,2k1δ),(mk2φ+j2π,2k2φ), (cos(mk1δ-(mk1/(m2-4))π),cos 2k1δ) 或 (cos(-mk1δ+(1+(mk1/(m2-4)))π),cos 2k1δ). 由 cos(mk1δ-(mk1/(m2-4))π)=cos(mk1δ), cos(-mk1δ+(1+(mk1/(m2-4)))π)=cos(-mk1δ) 及cos(mk1δ)=cos(-mk1δ)得:无论方程组(5)、(8)哪个有解,方程组(1)都有解为:(cos(-mk1δ),cos 2k1δ).类似解方程组(6)、(7)得方程组(1)另一相应的解为:(cos(-mk2φ),cos 2k2φ).当k1,k2为奇数时,类似得方程组(1)的解为:(cos(-mk1δ+π),cos 2k1δ),(cos(-mk2φ+π),cos 2k2φ);综上,m为奇数时,方程组(1)有上述1+(m2-5)/2+(m2+3)/2=m2个复数解;当m为偶数时,方程组(1)的复数解类似当m为奇数时的讨论步骤和方法可得. 定理2的证明当m为奇数时, Tm(y)=a0ym+0·ym-1+a2ym-2+0·ym-3+ a4ym-4+…+0·y2+am-1y, 代入方程组(1)得 Ry(f,g)=2m[-g(m+1)/2f(m-1)/2+(T2)2], 其中 T=Tm(x)+1,T2=-T2(x), f(m-1)/2=am-1+am-3T/2+…+a0(T/2)m-1/2, g(m+1)/2=am-1T/2+am-3(T/2)2+…+a0(T/2)(m+1)/2, Tm(y)=a0ym+0·ym-1+a2ym-2+0·ym-3+ a4ym-4+…+0·y2+am-2y2+am, 代入方程组(1)可得 Ry(f,g)=2m(gm/2)2, gm/2=am-T2(x)+am-2T/2+…+a0(T/2)m/2, T=Tm(x)+1,T2=-T2(x), 所以,∂(Ry(f,g))=2m·m/2=m2,则Ry(f,g)=0的全体复数根有m2个,且每个根至少为二重根,由于{x|Ry(f,g)=0}={x|gm/2=0},则gm/2=0的根包含Ry(f,g)=0的所有相异根.设xi(i=1,2,…,m2/2)为u(x)=0的m2/2个根,由于m为偶数,把xi代入方程组(1)得到其2个解为(xi,yi),(xi,-yi),则方程组(1)的相异解的个数至多为m2个. 定理3的证明方程组(2)中, Ry(f,g)=2[Tt(x)]2-Tm(x)-1, 注3 定理4证明类似定理1,不赘. 结论1的证明设 (9) (10) 式(9)-(10)得, m′(j1-j2)=t′(i1-i2), m′(j1-j2)=t′(i1-i2)+(k1-k2), 结论4的证明由结论3和引理2得 参考文献: [1] 周峻民,吴康.切比雪夫多项式的周期轨的相关研究[J].中国初等数学研究,2010(2):97-100. [2] 吴康.关于切比雪夫多项式的一些研究[J].中学数学研究,2006(3):27-30. [3] 刘适式,刘式达.特殊函数[M].北京:气象出版社,2002:304-332. [4] 北京大学数学力学系.高等代数[M].北京:人民教育出版社,1978:144-149.
(cos(-k2φ+2jk2π)/t,cosk2φ).



3 定理的证明

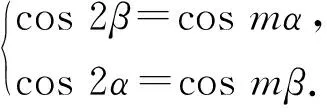
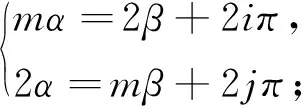
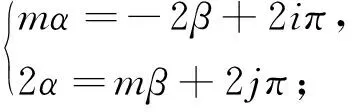
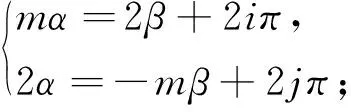
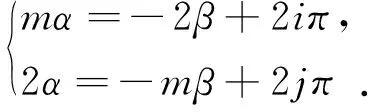
(mβ2/2+j2π,2(2i2-mj2)π/(m2+4)),
(-mβ3/2+j3π,2(mj3-2i3)π/(m2+4)),
(-mβ4/2+j4π,2(mj4-2i4)π/(m2-4)).
(-mk2φ-j2π,2k2φ),(-mk1δ-j1π,2k1δ),

∂([Tt(x)]2)=2t,∂(Tm(x))=m,