动手“做”数学，让学生放飞思维的翅膀——从教学案例谈动手做

☉江苏丰县初级中学 季明拓

动手“做”数学，让学生放飞思维的翅膀
——从教学案例谈动手做

☉江苏丰县初级中学 季明拓

苏教版教材遵循《数学课程标准》的理念，以“生活数学”、“活动思考”为主线展开课程内容，注重体现生活与数学的联系，为学生提供看得到、听得见、感受得到的基本素材；注重创设问题情境，引导学生在活动中思考、探索，主动获取数学知识，促进学生学习方式的转变，力求有效地实现《数学课程标准》中提出的“知识与技能，数学思考，解决问题，情感与态度”等四方面的课程总体目标.而本教材最大的特点是设置了“做”数学的栏目——“数学实验室”.引导学生通过“做”感受数学、探索知识和结论、应用所学知识解决简单问题.为此作为教师要善于激励引导学生去动手探究，展现问题的精彩，享受探究的乐趣，无疑对培养学生的学习和探究能力是大有益处的，今以笔者参加的一节评优课的设计为例，抛砖引玉，现身说法.

一、创设情境，回顾旧知

问题一：有一天，李老师的儿子从幼儿园放学来到办公室，看到郑老师办公桌上有一块平行四边形纸片，于是就拿起笔来画画，画了一会儿，对自己的作品不满意撕去了一些，巧的是刚好从A、C两个顶点撕开.如图1所示.你只有两把没刻度的直尺，你能帮它补好吗？

生：利用直尺过点A、C分别画BC、AB的平行线.

师：为什么所画的四边形是平行四边形？能说说你的依据吗？

生：根据平行四边形的定义，即两组对边分别平行的四边形是平行四边形.

（设计思路：通过问题情境，让学生动手画图复习回顾平行四边形的定义，这样一方面巩固学生的旧知，另一方面使学生知道平行四边形的定义既是性质，又是判定.）

师：同学们已经知道了平行四边形的定义，下面请同学们想一想平行四边形具有什么性质？

生1：平行四边形的对边平行.生2：平行四边形的对角相等.

生3：平行四边形的对角线互相平分.

师：同学们回答的很好，但请同学们回顾一下，在学习平行四边形的性质时我们是从哪几个方面研究的？

生：从平行四边形的边、角、对角线三方面研究的.

师：因此，我希望同学们在说平行四边形的性质时也按边、角、对角线的顺序叙述，这样便于记忆，具有条理性.下面请同学们用几何语言写出平行四边形的性质.

（设计思路：通过复习平行四边形的性质使学生了解研究四边形的问题常常从边、角、对角线三方面入手，也为下面探究平行四边形的判定打下伏笔.）

二、设疑导思，激活主体

问题二：学习了平行四边形后，小明回家用细木棒钉制了一个.第二天，小明拿着自己动手做的平行四边形向同学们展示.如图2所示.

小辉却问：你凭什么确定这四边形就是平行四边形呢？

大家都困惑了……

（设计思路：让学生主动从事想象、猜测、观察、实验、验证与交流等数学活动，使学生通过活动体会感受学习的乐趣，经历从多角度思考问题的过程.）

操作：学生分组讨论5分钟左右，然后全班交流讨论结果.

生1：我们小组利用两把直尺发现这个四边形的两组对边分别平行，所以我们根据平行四边形的定义得到这个四边形是平行四边形.

生2：我们小组利用三角板量出这个四边形的四条边的长度，发现它们的两组对边分别相等，所以我们认为这个四边形是平行四边形.

生3：我们小组利用三角板得到这个四边形的一组对边平行且相等，所以我们认为这个四边形是平行四边形.

生4：我们小组利用三角板得到这个四边形的一组对边平行，另一组对边相等，所以我们认为这个四边形是平行四边形.

（学生大胆发言，从不同角度思考得到了多种猜想，开阔了学生的思路，锻炼了发散思维的能力.）

师：同学们太棒了，大家采用不同的方法解决了问题，都认为自己的做法是正确的，但几何说理必须有理有据，你们各自的依据是什么呢？

（此问题的提出，引发了学生的讨论，课堂气氛活跃.）

生：我认为他们所说的六种方法只有第一位同学说得有理有据，他是利用平行四边形的定义得到的，其余方法都没有依据，只是一种猜想.

师：对，除第一种方法外其余方法都没有依据，只是一种猜想，那么他们所得的猜想是否正确呢？如何验证？

生：把所得猜想写成命题，然后证明此命题.

命题1：两组对边相等的四边形是平行四边形.

命题2：一组对边平行且相等的四边形是平行四边形.

命题3：一组对边平行、一组对边相等的四边形是平行四边形.

命题4：两组对角分别相等的四边形是平行四边形.

命题5：对角线互相平分的四边形是平行四边形.

（课堂上让学生自由发言，发表他们各自的看法，达成共识.学生在自由表达见解的宽松氛围中，体验了合作学习的乐趣.教师参与学生间的交流，倾听学生的想法，达到了学习的目的.）

操作：将学生分成5组分别证明命题，教师个别辅导，学生先做后相互交流，然后利用实物投影请学生展示证题过程.其中对于命题3，学生思维活跃，有不同解法.

生1：我在证明命题3时发现没法证明两三角形全等，它们满足的条件是边边角，所以命题3是错的.

生2：因为等腰梯形也满足一组对边平行、一组对边相等的条件，所以命题3是假命题.

师：通过刚才大家的操作、猜想、证明，我们已经得到了平行四边形的判定方法，我们仍然从边、角、对角线三方面考虑：

（1）根据定义：两组对边分别平行的四边形叫做平行四边形.

（2）两组对边分别相等的四边形是平行四边形.

（3）一组对边平行且相等的四边形是平行四边形.

（4）两组对角分别相等的四边形是平行四边形.

（5）两条对角线互相平分的四边形是平行四边形.

在今后的学习中我们可以用上述的五种方法证明四边形是平行四边形.

三、再创情境，明晰结论

问题三：有一天，李老师的儿子从幼儿园放学来到办公室，看到郑老师办公桌上一块平行四边形纸片，于是就拿起笔来画画，画了一会儿，对自己的作品不满意撕去了一些，巧的是刚好从A、C两个顶点撕开.如图3所示.通过本节课的学习，你能用几种方法帮它补好？（所用工具不限）

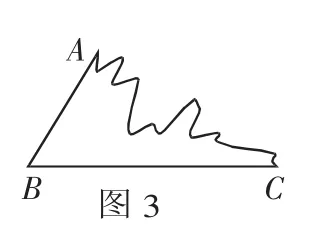
（设计思路：通过问题3再次巩固新知，小结本节课所学内容，并和问题1呼应.）

四、教学反思，总结提高

本课设计中，让学生经历猜想，再动手尝试、确认这一学习过程，然后通过质疑、思考、讨论，充分发挥学生的想象力和集体的智慧，发展学生的概括能力，不仅能更好地激发学生的学习兴趣，更重要的是培养学生的创新意识和创新能力.在实施开放式教学过程中，注重引导学生在课堂活动中通过“做”数学感悟知识的生成、发展与变化，培养学生主动探索、敢于实践、善于发现的科学精神以及合作交流的能力.将创新的教材、创新的教法与创新的课堂环境有机地结合起来，将学生自主学习与创新意识的培养落到实处.需要改进的是：对学生解题的时间安排得略紧一些，没有能充分展示学生的解题过程.