如何提高中考复习课的效率
☉江苏丹阳市第八中学 王仲庆
如何提高中考复习课的效率
☉江苏丹阳市第八中学 王仲庆
教研背景:中考数学复习是初中学生进行系统学习的最后阶段,所跨越的时间长,涉及的知识面广,因此每年都会引起广大师生的高度重视.如何在漫长的复习阶段,既不让学生产生厌学的情绪,又可将学生的知识结构进行优化,提高他们的思维水平和认知能力,是我们面临的一个重要课题.下面我们选取《锐角三角函数的复习》这节课,谈谈对中考数学复习评讲课的新认识.
一、注重提问的实效性
在中考数学复习阶段,因为很多都是知识的再现过程,所以教师的提问更要避免简单的一问一答式的提问,注重提问的方式和技巧.

师:要求AC的长度,可以利用的直角三角形有哪些?
生1:在Rt△ACD中,利用特殊角的三角函数知识来解决.




其他教师在上这节复习课时,很多教师都会一开始提问:锐角三角函数是怎么定义的?特殊角的三角函数值是多少?学生回答:(1)锐角A的正弦、余弦和正切都是∠A的三角函数;(2)特殊角有30°、45°、60°,它们的三角函数值分别为……
很显然,这种提问只是一种知识的简单重复和记忆,学生不用动任何脑筋即可回答,自然没有兴趣,也不利于学生的思维发展.而[片段一]巧妙地将直角三角形的函数关系蕴涵于一个题目当中,让学生从不同的角度观察解决问题,让学生真正理清锐角三角函数之间的关系,加深了对特殊角的三角函数值的记忆,开拓了学生的思维,有很强的实效性.
二、注重数学内在本质的揭示
新课程标准提倡数学问题生活化、情境化,近年来中考也出现了大量蕴涵实际生活情境的问题,注重考查学生学数学、用数学的能力,但很可惜,这类题目的得分率都不高.究其原因,就是我们在平时教学中忽略了对数学本质的揭示,缺乏对数学知识内在联系的挖掘和对学生数学抽象思维的培养.
[片段二]如图2,小明想测量古塔CD的高度,他在A处仰望塔顶C,测得仰角为30°,再往塔的方向前进50m至B处,测得塔顶C的仰角为45°,那么该古塔有多高?(小明身高忽略不计,结果精确到1m)

师:请同学们思考,在哪个三角形中利用三角函数求古塔CD的高度呢?
生:可以在Rt△ADC或Rt△BDC中.
师:图中两个直角三角形除了给出特殊角外,还缺少什么条件?它们有什么内在的联系?
生:都缺少一条已知边,但他们有一条公共的直角边CD,我们可以设BD为x,用x的代数式表示AD,再利用公共边CD找相等关系.
师:也就是说只要抓住“古塔的高”这一固定量,再利用三角函数关系求塔高.同学们,这样的问题在我们生活中还有很多,让我们再看下面两道题,观察它们之间的特点,有哪些类似的地方?
补充1:如图3,河旁有一座小山,从山顶处测得河对岸点C的俯角为30°.测得岸边点D的俯角为45°,又知河宽CD为50m,现需从山顶A到河对岸C拉一条笔直的缆绳.求缆绳AC的长.(答案可带根号)
分析:根据俯角的定义,知AE平行于CD,得到∠C=30°,∠ADE=45°,从而转化为上一类问题.


分析:过C点作垂线,再由对顶角定义转化为上一类问题
在学生回答完以后,反过来思考知识之间的内在联系,教师通过对题目的补充,揭示其本质,加深了学生对锐角三角函数应用方法的理解.同时教师注重数学内容的延伸,抓住数学内容的本质,这样必能促进学生数学思维的发展和解题能力的提高.
三、注重数学思想方法的教学
数学学习贯穿着两条主线,即数学知识和数学思想方法.通性通法蕴涵着丰富的数学思想和方法,更贴近学生的认知水平,符合常人的思维习惯,同样也利于培养学生的数学能力.在初中数学中,常用的数学思想有函数和方程的思想、数形结合思想、分类讨论思想、化归转化思想、整体处理思想等.
[片段三]如图5,某居民小区有一朝向正南方向的居民楼,该居民楼的底楼是高8m的小区超市,超市以上是居民住房.在该楼的前面15m处要盖一栋高20m的新楼.当冬季正午的阳光与水平线的夹角为30°时,问:超市以上的居民住房采光是否受影响,为什么?
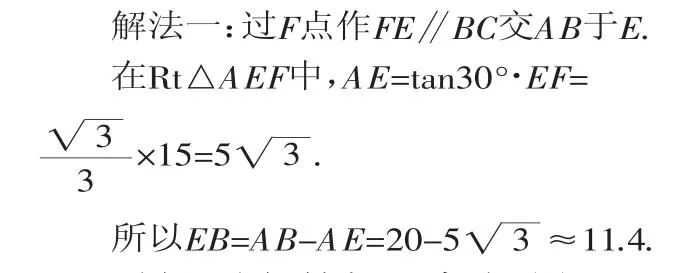

则太阳光投射点F距离地面约11.4m,高于8m的超市.
即超市以上的居民住房采光不受影响.
解法二:如图6,延长AF交BC所在直线于G点.


所以CF≈11.4.
则太阳光投射点F距离地面约11.4m,高于8m的超市,即超市以上的居民住房采光不受影响.
解法三:假设太阳光投射点F距离地面8m处,即CF=8.
过F点作FE∥BC,可得矩形EBCF,
所以BE=CF=8,所以AE=AB-BE=12.
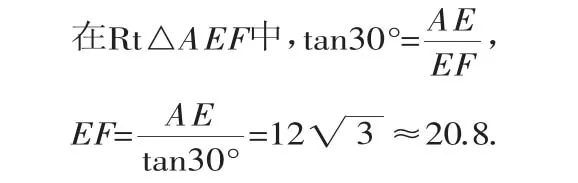

则两楼间距离BC为20.8m,而图中BC的距离为15m,所以超市以上的居民住房采光不受影响.
[片段四]的探究题,教师通过引导学生从数和形的角度来解决问题,很好地发展了学生函数思想和数形结合的思想,同时也渗透了数学分类的思想方法.在平时的教学复习中,我们应在解决问题的过程中对这些数学思想加以揭示、运用和提炼,并在专题复习阶段加以强化训练.另外还要注意通性通法,以提高学生的思维水平和解题能力.
四、加强变式练习的教学
在中考数学复习教学中,解题训练是极为重要的,但习题演练的关键不在题量,不是简单机械的重复训练和题海战术,而应该有一定的系统性、针对性,有明确的考查目标和培养方向.在平时教学中,我们应该多对一个已有的习题进行系列改编变式,形成一个题组或题链.
[片段五]如图8,正方形ABCD中,E是BC边上一点,以E为圆心、EC为半径的半圆与以A为圆心、AB为半径的圆弧外切,则sin∠EAB的值为___________.
解:设大圆半径为R,小圆半径为r,则AE=R+r,BE=R-r.


变式1:若在圆心角为90°的扇形中,⊙A、⊙B分别与扇形两两相切,则tan∠BAO的值为_______.
解:设⊙A的半径为r,⊙B的半径为R,则OA=R-r,OB=R+r.


变式2:以正方形ABCD的BC边为直径作半圆O,过点D作直线切半圆于点F,交AB边于点E,则三角形ADE和直角梯形EBCD周长之比为________.
分析:周长问题转化为线段问题,线段问题转化为方程问题.
即周长之比→求EF→列关于EF的方程.


在平时的复习教学中,我们若能经常这样来设计一定量相互衔接和过渡的,具有知识、能力层次、梯度要求的变式问题,必能优化学生的知识结构,提升学生灵活应用知识、分析问题、解决问题的能力.
案例反思:
透视本教学案例,我们不难发现,新课程教学要求我们数学教师应该创造性地利用和开发教学资源,应该将课堂与生活实际紧密联系起来,体现数学来源于生活,提高运用知识解决实际问题的能力;要求我们教师要善于挖掘数学内容的内在联系,揭示其本质,同时注重数学思想方法的渗透,加强变式训练,提高数学复习课的质量和效率.

