中考压轴题——在运动中分析,在变化中求解
☉江苏淮安生物高等职业学校 刘 江
中考压轴题
——在运动中分析,在变化中求解
☉江苏淮安生物高等职业学校 刘 江
在2011年的中考试题中,有很多省市都以动点型试题作为压轴题.这样的试题及代数与几何等众多知识于一题,考查了学生的数学思维能力、空间想象能力和数学创新意识以及初步的辩证唯物主义观点.
很多学生在平时的学习中疏于用变化、运动的观点分析几何图形,难于驾驭这类问题.解决这类问题应理清图形的变化过程,正确分析变量与其他变量之间的内在联系,建立变量与其他变量之间的数量关系.本文以2011年全国各地的中考动点型压轴题为例进行归纳分析,供初三学生复习参考之用.
一、动点与列函数关系式相结合
例1(江苏宿迁)如图1,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F.
(1) 当t≠1时,求证:△PEQ≌△NFM;
(2)顺次连接P、M、Q、N,设四边形PMQN的面积为S,求出S与自变量t之间的函数关系式,并求S的最小值.
解:(1)因为四边形ABCD是正方形,


点评:此类题是中考中常见的一类题,利用变量列函数关系式,要分析图像的变化过程及条件,理解图像的性质,弄清各个条件的内在联系及数量关系,经常利用的几何知识有平行线分线段成比例、相似三角形性质、与圆有关的性质定理、勾股定理、面积公式等.
二、动点与坐标系相结合
例2 (浙江湖州)如图2,已知正方形OABC的边长为2,顶点A、C分别在x、y轴的正半轴上,M是BC的中点.P(0,m)是线段OC上一动点(C点除外),直线PM交AB的延长线于点D.
(1)求点D的坐标(用含m的代数式表示);
(2)当△APD是等腰三角形时,求m的值;
(3)设过P、M、B三点的抛物线与x轴正半轴交于点E,过点O作直线ME的垂线,垂足为H(如图3).当点P从点O向点C运动时,点H也随之运动.请直接写出点H所经过的路径长.(不必写解答过程)

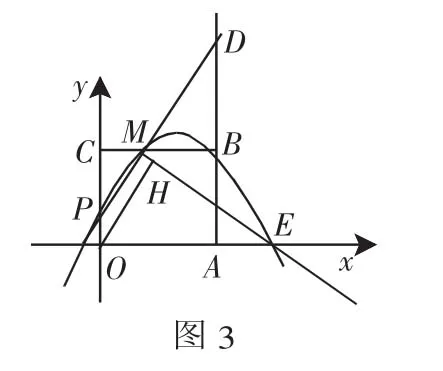

评析:动点与坐标系相结合的题型,将几何图形置于坐标系中,让动点带动某一个或几个几何图形运动,在这一运动变化过程中,研究、探讨图像的位置关系,利用函数与几何知识进行解答,它考查的知识点多,综合性强,对学生的能力提出了更高的要求.
同时,在解动点问题的时候,要学会分类讨论,要通过观察、比较,分析图像的变化,解释图像之间的内在联系,要能够根据条件作出或画出图形,从而进行分类.

