信息技术与初中数学教学整合几点建议

☉浙江宁海县潘天寿中学 陈建华

信息技术与初中数学教学整合几点建议

☉浙江宁海县潘天寿中学 陈建华

随着教改、课改的不断深入，多媒体信息技术逐渐走进课堂.多媒体信息技术的出现为初中数学教学手段的改进与优化提供了新的机遇，多媒体信息技术与初中数学课堂教学进行有效的整合能够实现许多理想的效果.但在其过程中更要注重并科学处理好教学内容、学习方式、教学方式等几个关系，恰当而有用地使用信息技术，才能提高教育教学质量，提高学生学习兴趣和参与意识.

信息技术；初中数学；整合；建议

大力推进信息技术在初中数学教学过程中的普遍应用，逐步实现教学内容的呈现方式、学生的学习方式，以及教学过程中师生互动方式的变革，充分发挥信息技术的优势，为学生的学习和发展提供丰富多彩的教育环境和有力的学习工具，已成为初中数学教学改革的一种必然选择.那么，在初中数学教学中如何利用信息技术呢？如何实现信息技术与初中数学教学的整合呢？现在教学实践中针对信息技术与初中数学教学的整合，谈谈几点建议.

一、准确把握信息技术的使用时机

如果信息技术的使用仅仅是替代了教师更多的传递工作，信息技术的参与并没有使教学方法得到根本的改变，学生的学习仍然处于被动的学习状态，学生学习的主体性没有得到体现和落实，这就是违背教育教学改革的初衷，“人灌”变成了“电灌”，是资源的浪费.因此信息技术与初中数学教学的整合应从教学实际出发，准确把握信息技术的使用时机.

案例一：“解斜三角形”的研究.

在学习了正弦定义和余弦定义后，在研究“已知两边和其中一边的对角，求三角形其余两角”的问题时，提出如下两个问题：

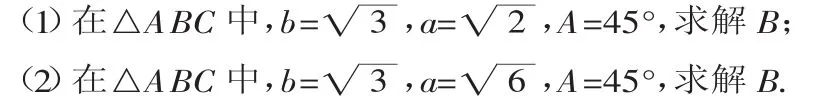
在学生求解后，发现问题（1）有两个解，而问题（2）只有一个解，这是为什么呢？接着提出更一般的问题：“在△ABC中，已知a，b，锐角A，求三角形的解的个数”.学生对这个问题会感到无从下手，这时，引导学生用“几何画板”来研究.

分析：可通过作三角形的办法来确定三角形的解的个数.

制作：①打开“几何画板”软件，用［画点］工具画点A；

②用［画射线］工具画两条射线AM、AN，并在射线AM上取点 C，记 AC=b；

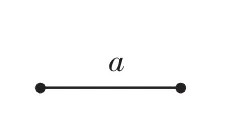
③用［画线段］工具画线段a；

④用［画圆］工具以点C为圆心，a为半径画圆；

⑤过点C作射线AN的垂线，垂足记为点D；

⑥用［画线段］工具画线段CD，隐藏垂线，（如图1）.

演示课件：改变圆的大小，观察圆与射线AN的交点情况.

结论：（1）当 a＜bsinA 时，三角形无解；

（2）当a=bsinA或a≥b时，三角形有一个解；

（3）当 bsinA＜a＜b时，三角形有两个解.

二、不要忽视学生的主体作用

充分发挥学生的主体作用，这是信息技术与数学教学整合的基本原则，也是现代教育思想下师生关系的重要转变.教学中，教师的教、课件的制作、媒体的使用，都要为学生的学服务，要关心教学价值，遵循教学原则，体现教学目标.有些教师制作的数学课件，背景画面复杂，几何图形变幻莫测，按钮奇形怪状，并且使用大量的动画和音响.这些课件画蛇添足、喧宾夺主，分散了学生的注意力，冲淡了他们对学习重点、难点的关注，久而久之，学生必然会产生厌倦情绪，反而不利于学习兴趣的激发.教师应在实际教学中系统考虑教学活动诸要素和环节的相互作用，在教学过程中运用多种方式优化教学，激发学生积极参与.学生可以利用自己所掌握的信息技术，在数字化学习环境中进行数学实验，亲身体验知识再发现的过程.目前数学软件“几何画板”和“Z＋Z”智能教育平台的深入开发和广泛使用，使这种课型越来越受到教师和学生的欢迎.

案例二：在学习《探索勾股定理》时，让学生利用“几何画板”作一个动态变化的直角三角形，通过度量各边长度的平方值并进行比较，学生对直角三角形三边关系产生很感性的认识；通过观察，学生发现任何一个直角三角形的两直角边的平方和等于斜边的平方，从而加深了对勾股定理的认识、理解和应用.这种让学生动手操作、观察、探究的教学效果远比传统教学来得高效，很受学生的欢迎.

案例三：在讲《可能性》一章做“转盘游戏”时，学生一般制作的转盘做得比较粗糙，转动不灵活，这样就影响了游戏的公平性，而且我们有时候可能需要转动50次、100次，甚至更多，才能估计出结果，这样会带来很多不便.但是使用“Z+Z”智能教育平台，就可以避免这些问题.在“Z+Z”智能教育平台，每个学生都可以用它制作一个转盘，模拟转盘的转动，并随机停止，在编辑框中显示转盘转动的次数，当电脑完成这些操作时，它会将在不同区域内的数据统计成表格，让学生真实感受转盘游戏的真实性，体验“做数学”的乐趣.

三、信息技术运用与传统教学要做到平衡

把信息技术引入数学教学后，不是信息技术用的越多越好，计算机作为有效的辅助工具是为教学服务的，要把它用得恰到好处.传统教学的优势应该保留，如教师的示范作用、教师与学生之间富于人情味的及时交流，教师组织起来的探究问题的活跃氛围等.理想的教学应该是把教师与信息技术的优势同时充分发挥出来，把信息技术与传统媒体完美地结合在一起，把握好纸笔运算、推理、作图与信息技术的使用之间的平衡.

案例四：八年级第一学期几何证明中的选学内容“三角形中的边角不等关系”.

有一位教师用几何画板制作简单动画进行实验：在等腰三角形中，一腰变长，观察其所对的角的大小如何变化.学生观察得出：等腰三角形一腰变长，其所对的角也变大.我马上进行测量，再变化腰长，再测量.学生进一步肯定：只要腰变长，其所对的角就要变大.

科学家们在发明创造时就是不断地进行试验，几何画板也为学生提供了一个数学实验平台，帮助学生猜测结论，从而激发学生去验证，多次试验看是否有相同结论.

在开始设计定理的证明时，教师制作了证明方法的动画，预期效果是：学生想到沿角平分线翻折，我用动画来解释这种思维方法.课堂上总觉得是学生被老师牵着走，甚至部分学生思维停滞，不明白为什么要看这个动画.

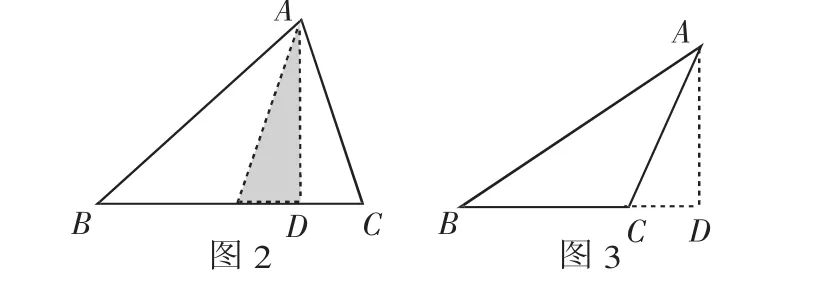
教师做了这样的修改：在证明命题之前，学生通过动手折纸验证结论的正确性，这样就为接下来的证明作了很好的铺垫.果然经过操作后，学生证明方法很多，证明的过程很顺利，可其中有一种证明是不完整的：在操作中，学生沿着边BC上的高翻折，成功地比较了两角的大小（如图2），在证明时却有如图3的情况，三角形ABC中，BC的高在三角形外.课堂上，学生很快想到了分类讨论进行证明，成功地解决了这个问题.

在证明后，教师和学生一起将学生的证明方法进行了总结.三种方法都是类比等边对等角证明的思想方法——翻折，其中两种方法是沿着角A的平分线翻折（如图4、图5），一种方法是沿BC上的高翻折（如图6），学生边看动画演示，边思考.同时教师提出问题：为什么沿BC翻折要讨论？学生很快找到了问题的根源：三角形的高是否在三角形内部，要看三角形的形状.

这次动画演示成功地类比了等边对等角证明的思想，将几种证明方法进行归类，学生找到了思维的方向，使得信息技术运用于课堂教学中有一次质的提升.在上述的几个案例中，试想如果学生掌握了《几何画板》软件的使用方法，学生能自行设计出这样的辅学环节，那么学生对相关知识的掌握更加扎实，学生学习的主动性、学习的思维能力也会得到明显的提高，学生探究能力的发展也就成了可能.

综上所述，多媒体技术的应用为数学教学注入了新的生命力，多媒体技术与数学教学的有机结合是数学教学改革中的一种新型教学手段.目前，信息技术与初中数学教学的整合正处于初级阶段，教师可在具体教学过程中，根据自己的认识水平和学校的现有条件，选择性地进行数学课堂教学的整合实践，摸索出行之有效的整合方法.