函数最值问题探微
☉江苏兴化市板桥初级中学 张仁荣
函数最值问题,是函数中的热点问题,如求利润的最大值,费用的最小值等问题中常会出现.解决此类问题要构建合理的函数模型,将实际问题数学化并运用函数知识解决问题.
一、构建一次函数模型解决实际问题中的最值问题
一次函数的单调性受比例系数k影响,当k>0时,y随着x的增大而增大;当k<0时,y随着x的增大而减小.所以一次函数在定义域内并无最大值或最小值,但在实际问题中一次函数的自变量的取值有一定的范围,所以可以根据此范围结合函数的单调性来求解最值问题.
例1 某电器商城“家电下乡”指定型号冰箱、彩电的进价和售价如下表所示:
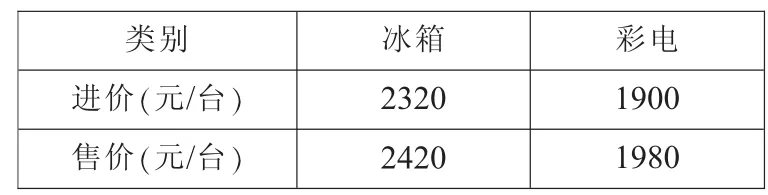
类别 冰箱 彩电进价(元/台) 2320 1900售价(元/台) 2420 1980
(1)按国家政策,农民购买“家电下乡”产品享受售价13%的政府补贴.农民田大伯到该商场购买了冰箱、彩电各一台,可以享受多少元的补贴?

分析:由题可知商场的利润等于销售冰箱的利润和销售彩电的利润之和,所以根据“单件利润×数量=总利润”找出总利润y与x间的函数关系式.最后根据一次函数的单调性,求出函数的最值,从而解决问题.
解:(1)(2420+1980)×13%=572.
(2)①设冰箱采购x台,则彩电采购(40-x)台,根据题意得:
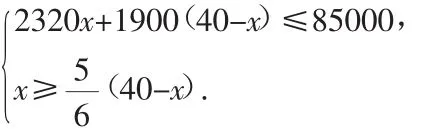
因为x为整数,所以x=19、20、21.
方案一:冰箱购买19台,彩电购买21台.
方案二:冰箱购买20台,彩电购买20台.
方案三:冰箱购买21台,彩电购买19台.
设商场获得总利润为y元,则:

因为20>0,所以y随x的增大而增大.
所以当x=21时,y最大=20×21+3200=3620.
点评:构建一次函数模型解决实际问题中的最值问题,关键要注意两点:一要根据一次函数的单调性,二要求出一次函数的自变量的取值范围.根据函数的单调性求出函数的最大值或最小值,从而解决实际问题.
二、构建二次函数模型解决生活中利润最大值问题

例2 今年我国多个省市遭受严重干旱.受旱灾的影响,4月份,我市某蔬菜价格呈上升趋势,其前四周每周的平均销售价格变化如下表:


(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接写出4月份y与x所满足的函数关系式,并求出5月份y与x所满足的二次函数关系式.

分析:由题意可知,4月份销售利润=销售总价-成本,满足一次函数关系,可以根据一次函数的性质求出最大值;5月份的销售利润与x满足二次函数关系,可以借助二次函数的顶点坐标求出函数的最大值,解决利润最大值问题.
解:(1)4月份y与x满足的函数关系式为y=0.2x+1.8.

所以五月份y与x满足的函数关系式为y=-0.05x2-0.25x+3.1.
(2)设4月份第x周销售此种蔬菜1千克的利润为W1元,5月份第x周销售此种蔬菜1千克的利润为W2元.

因为-0.05<0,所以W1随x的增大而减小.
所以当x=1时,W1最大=-0.05+0.6=0.55.

所以x>-0.5时,y随x的增大而减小.
所以当x=1时,W2最大=1.
所以4月份销售此种蔬菜1千克的利润在第1周最大,最大利润为0.55元;5月份销售此种蔬菜1千克的利润在第1周最大,最大利润为1元.
点评:在实际问题中,如果两变量满足二次函数关系时,可构建二次函数模型并通过对二次函数的最值的求解,解决实际中的最值问题.
函数的最值问题在实际运用中比较广泛,也是学习中的重点内容,解题的关键要从实际生活中抽象出数学模型,将实际问题数学化通过对数学知识的求解,来解决实际问题.

