一种多元素多尺度形态非抽样小波分解方法

王冰,李洪儒,许葆华

(军械工程学院 导弹工程系，石家庄 050003)

轴承故障在电动机故障中占有很大比例。当轴承存在局部缺陷时，其振动信号中的脉冲信号含有丰富的缺陷信息，如果能够有效地将缺陷引起的脉冲信号提取出来，便可以诊断出缺陷存在的部位[1-4]。

包络分析与小波包分解是目前常用的滚动轴承故障特征提取方法[5-6]，但包络分析需要预先确定带通滤波器的中心频率和频带；而小波包分解在本质上仍是一种基于频率的线性分解，且存在各频带能量交叠现象。因此，对于具有非线性非平稳特征的轴承故障信号，这两种方法很难取得理想的效果。

基于此问题，文献[7-8]提出了形态小波(morphological wavelet，MW)的概念，成功地将大多数线性小波和非线性小波统一起来，形成了多分辨分析的统一框架。但该形态小波在信号分解时会出现逐层信息减半的情况，且在本质上是Haar小波，因此重构信号不够平滑。文献[9]提出一种形态非抽样小波(morphological un-decimated wavelet，MUDW)分解方法。文献[10]利用数学形态学算子构造了MUDW的一般框架。文献[11]则基于该框架提出形态开运算、闭运算级联的组合滤波器方法，并将该方法应用到复杂锥筒振动信号特征提取中，取得了很好的效果。文献[12]利用多尺度形态开闭滤波代替文献[11]中的单尺度组合滤波，并依次提取了主减速器振动特征。文献[13]构造了一种基于多尺度差值形态滤波的形态非抽样小波分解方法，并将其应用到滚动轴承故障特征提取中，取得了比传统小波包分解更好的效果。文献[14]构造了一种具有2部分的形态非抽样小波分解算子，前一部分用形态开闭和闭开的混合滤波器平滑噪声，后一部分用形态差值算子提取冲击特征，取得了较好的效果。

在此，根据滚动轴承故障信号的特点，在MUDW的一般框架内，提出了一种多元素多尺度形态非抽样小波分解算法，并应用该方法对电动机轴承典型故障信号进行分析。

1 形态非抽样小波理论

1.1 数学形态基本变换

基本数学运算包括腐蚀、膨胀、形态开和闭运算[15]。设f(n)和g(n)分别为定义在集合F={0,1,…，N-1}和集合G={0,1,…,M-1}上的离散函数，且N≥M。其中，f(n)为原始信号，g(n)为结构元素，则f(n)关于g(n)的形态腐蚀和形态膨胀算子分别定义为

(fΘg)(n)=min{f(n+m)-g(m)}，m=0,1,…,M-1；

(1)

(f⊕g)(n)=max{f(n-m)+g(m)}，m=0,1,…,M-1；

(2)

f(n)关于结构元素g(n)的形态开和闭运算分别定义为

(f∘g)(n)=(fΘg⊕g)(n)，

(3)

(f·g)(n)=(f⊕gΘg)(n)，

(4)

式中：Θ和⊕分别表示腐蚀和膨胀运算;∘和·分别代表f(n)关于结构元素g(n)的形态开和闭运算。

1.2 形态非抽样小波变换

形态非抽样小波克服了传统形态小波因抽样引起的不足，是一种基于数学形态学的信号多分辨率分解理论。

1.2.1 金字塔条件和对偶小波分解

形态非抽样小波分解中具有分析算子和合成算子，且必须满足金字塔条件[7-8]

(5)

(6)

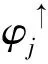
金字塔条件保证在分析和合成这两个连续的步骤中，没有信息的损失。基于金字塔条件，可以构造对偶小波分解。单层对偶小波分解框架如图1所示，多层对偶小波的分解方法与其类似。

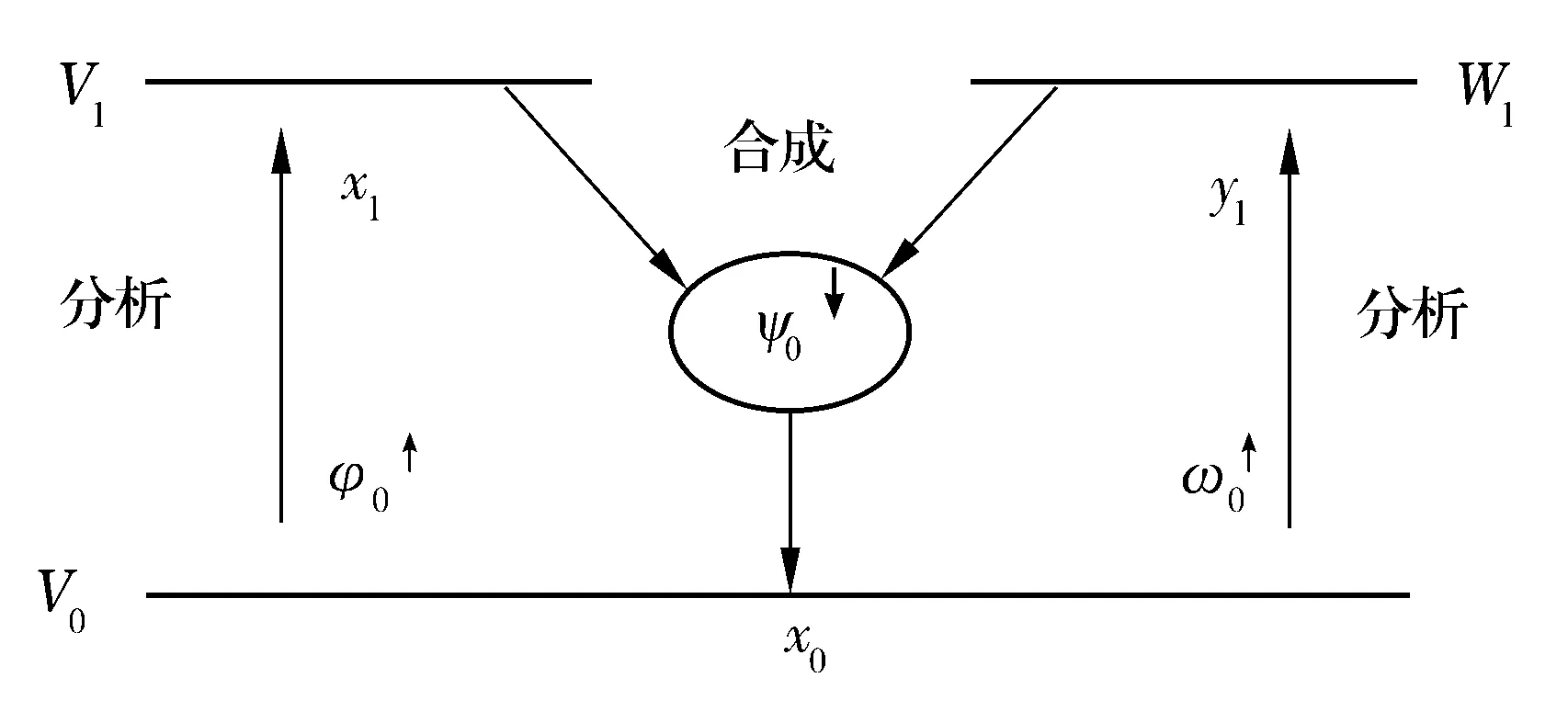
图1 单层对偶小波分解框架示意图

1.2.2 形态非抽样小波一般框架及算法

形态非抽样小波构造方法的一般框架可描述为

(7)

(8)

T(xj)+(id-T)(xj)=id(xj)，

(9)

式中：T()为数学形态算子。可以根据信号处理的不同需求选择基本形态算子或某种组合形式。

现有文献中的形态非抽样小波算法均基于形态非抽样分解框架建立，设形态学膨胀算子为δ，腐蚀算子为ε，闭算子为φ，开算子为γ，现有文献中阐述的算法的信号分析算子见表1。

表1 现有文献中形态非抽样小波算法

其中，文献[12]和[13]中的信号分析算子为多尺度形态学变换，算法中每层小波分解对应某一尺度的结构元素(j+1)g0，其优点在于逐层分解后得到的近似信号和细节信号的物理意义更明显，即对应于利用相应尺度的结构元素进行形态运算得到的结果。

文献[9]和[14]的信号分析算子均由两部分组成，以文献[14]为例，算子中的前一部分0.5(γφ+φγ)为典型的形态学组合滤波器，可同时去除信号中的正负噪声[16]。后一部分(φ-γ)为形态差值滤波器，可同时提取信号中的正负冲击。该算法的优点在于其每一层小波分解既能够平滑噪声，又能够有效地提取冲击特征。

在基于数学形态学的处理方法中，结构元素的形状和大小是影响性能的关键。对于白噪声，半圆形结构元素可以取得较好的滤波效果；对于脉冲噪声，一般采用三角形结构元素进行滤波[17]。在基于形态学的周期性脉冲提取时，扁平直线形结构元素效果最好，一般选取直线形结构元素的长度为0.6T(T为故障周期)[18]。

因此，在构造形态非抽样小波分解的信号分析算子时，需根据实际情况确定结构元素的类型和大小，文献[14]在不同分解层次使用不同长度的结构元素，但在分析算子的前后两部分使用同一种结构元素，灵活性和针对性略显不够。

1.2.3 多元素多尺度形态非抽样小波

着眼于提高分析算子的有效性和灵活性，提出一种多元素多尺度形态非抽样小波分解方法，其分解算子为

1)g0)(δ-ε)(xj,(j+1)g1)，

(10)

(j+1)g0)(δ-ε)(xj,(j+1)g1),

(11)

(12)

该分解算子包括0.5(γφ+φγ)(xj,(j+1)g0)和(δ-ε)(xj,(j+1)g1)两部分。第1部分为使用三角形结构元素的多尺度形态开闭和闭开交替混合算子，可以平滑信号且抑制噪声。第2部分为使用扁平形结构元素的多尺度形态梯度算子，可以有效地提取信号的冲击特征。其中，每个尺度λ对应的形态学变换采用的结构元素分别为

λg0=g0⊕g0⊕…⊕g0，

(13)

λg1=g1⊕g1⊕…⊕g1，

(14)

式中：λ为不同尺度的大小；g0和g1分别为λ=1时的三角形和扁平形结构元素。

2 仿真分析

为验证多元素多尺度形态非抽样小波提取信号冲击特征的有效性，进行了仿真分析，设仿真信号为

x(t)=3x1(t)+0.3x2(t)+i(t)，

(15)

式中：x1(t)为周期性的指数衰减冲击信号，冲击频率为16 Hz，每周期内冲击函数为e-200t·sin(288πt)；x2(t)为谐波信号，x2(t)=cos(2π×25t)+cos(2π×50t)；i(t)为标准差为1的高斯白噪声。信号采样频率为1 024 Hz，采样时间为1 s，仿真信号的时域波形和频谱如图2所示。

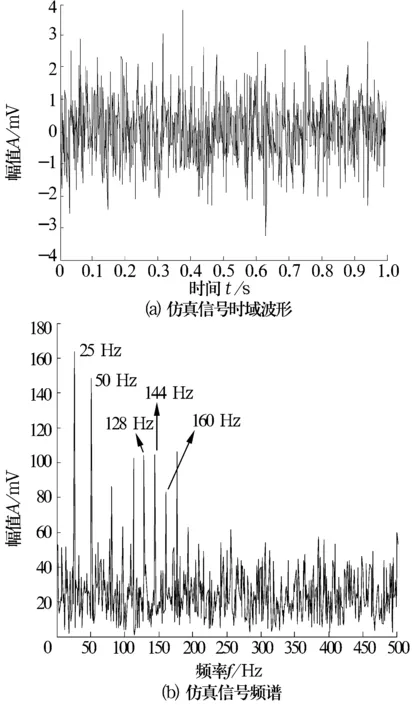
图2 仿真信号时域波形及其频谱

从频谱图可以看出， 25和50 Hz的谐波干扰成分比较明显，且以144 Hz为中心出现一组频宽约为16 Hz的边频序列。而16 Hz及其倍频的冲击成分由于谐波成分的抑制以及噪声的干扰，很难在频谱中反映出来。为了提取信号的冲击成分特征，必须选取合适的方法抑制谐波及噪声。

为分析文中方法的正确性和有效性，将其与典型的多尺度形态差值非抽样小波分解方法[13]和固定结构非抽样小波分解方法[14]进行分析对比。为定量分析各形态非抽样小波分解方法抑制谐波噪声干扰以及提取周期性脉冲信号的能力，采用了低频能量比Q和特征能量比R的概念[19]。低频能量比Q用以描述非抽样小波分解方法抑制谐波干扰的能力，Q=C/E，其中C为谐波频率能量值，E为特征频率能量值。低频能量比Q越低，抑制谐波干扰的能力越强。特征能量比R可以描述非抽样小波提取冲击频率的性能，R=(E1+E2+…+En)/E，En为解调后的信号频谱在n倍频处的能量值，文中n=5。特征能量比R越大，提取冲击频率的能力越强，效果越好。

2.1 多元素多尺度形态非抽样小波分解方法

选择三角形结构元素g0={0 1 2 4 2 1 0}，扁平形结构元素g1={0 0 0 0 0}，对仿真信号进行2层分解，并对第2层近似信号进行频谱分析，结果如图3所示，可以看出，冲击频率及其倍频被清晰地解调出来。经计算，该分解方法的特征能量比R=0.413 7，低频能量比Q=0.210 5。

图3 多元素多尺度形态非抽样小波分解结果

2.2 多尺度形态差值非抽样小波分解方法

选用扁平形结构元素g={0 0 0 0 0}对仿真信号进行2层分解，其中第2层近似信号的频谱如图4所示。从图中可以看出，冲击频率16 Hz及其倍频被解调出来，与图3相比，其噪声干扰要更加明显。经计算，该分解方法的特征能量比R=0.253 0，低频能量比Q=0.200 6。

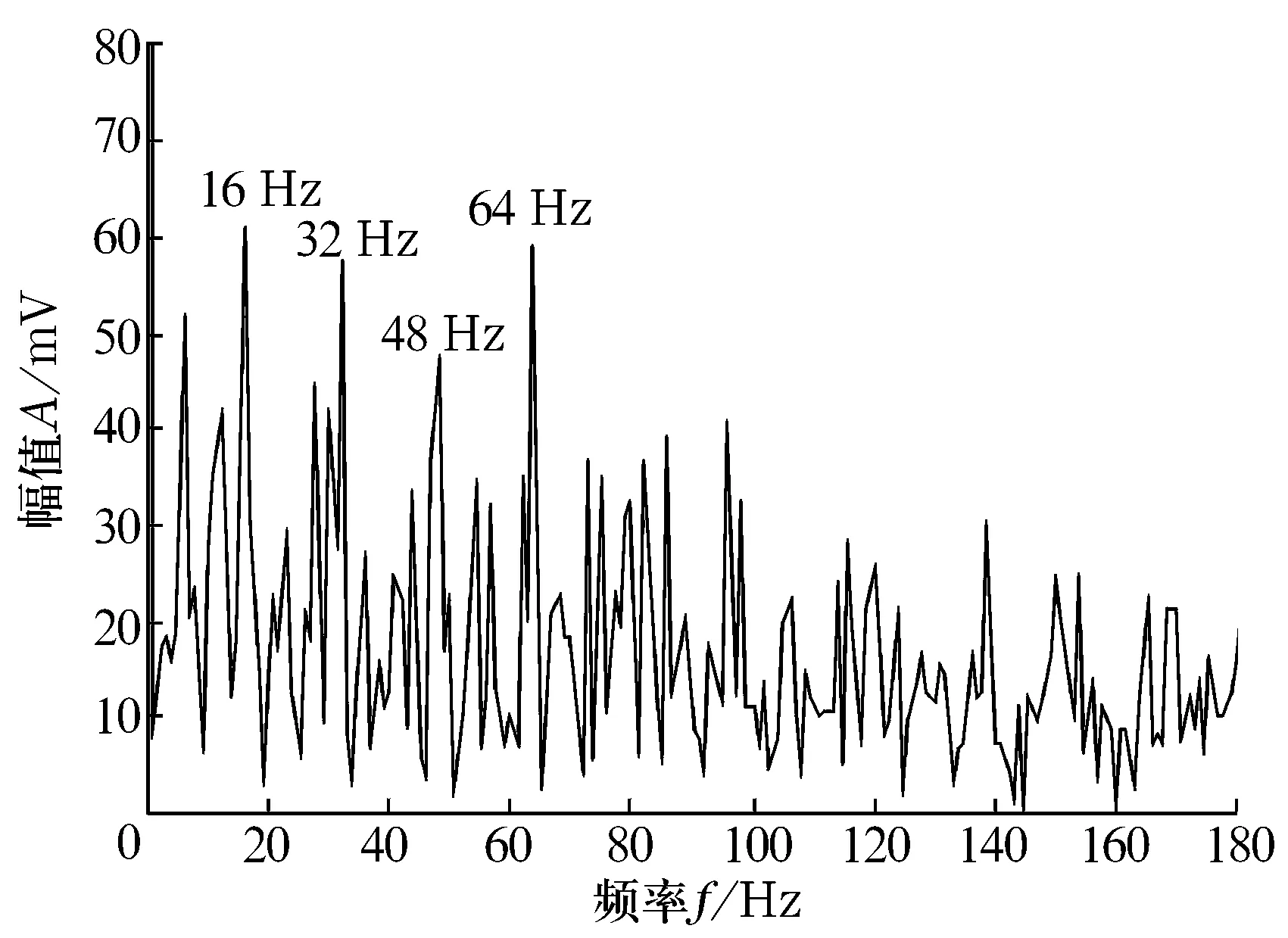
图4 多尺度形态差值非抽样小波分解结果

2.3 固定结构非抽样小波分解方法

分别采用三角形结构元素g={0 1 2 4 2 1 0}和扁平形结构元素g={0 0 0 0 0}对仿真信号进行2层分解，并在此基础上获取第2层近似信号的频谱图，结果如图5所示。

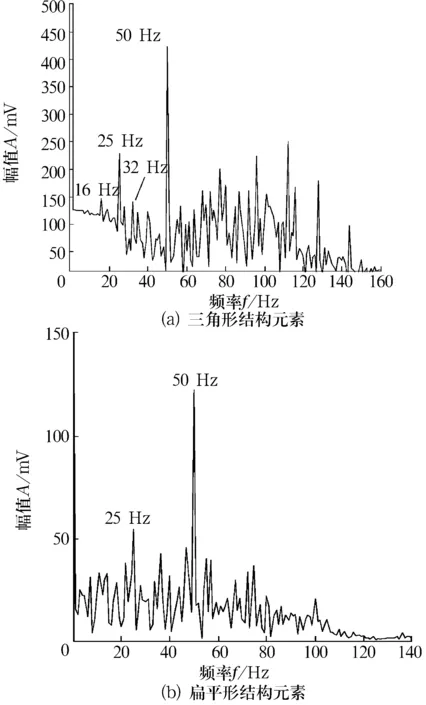
图5 固定结构非抽样小波分解结果

由图5a可以看出，冲击频率16 Hz及其倍频没有被提取出，而谐波频率25 Hz和50 Hz的谱线异常明显。此时特征能量比R=0.175 3，低频能量比Q=0.647 7。由此可知，选用三角形结构元素进行分解时，该方法对于冲击频率的特征提取能力较差，抗谐波干扰能力也不强。从图5b中几乎看不出冲击频率，而谐波频率25 Hz和50 Hz的谱线更加明显。此时特征能量比R=0.404 2，低频能量比Q=0.831 5，由此可知，选用扁平形结构元素时，该方法的效果依旧不理想。

2.4 结果分析

纵向分析上述仿真试验中的R和Q值，结果见表2。由于对分解算子的不同部分使用不同类型的结构元素，多元素多尺度形态非抽样小波分解方案具有最高的特征能量比和较低的低频能量比，体现了优良的抑制谐波噪声和冲击频率提取效能；多尺度形态差值非抽样小波方案在每一层分解时由于没有进行滤波，导致对噪声的抑制能力较弱，因此特征能量比R相对较低；固定结构非抽样小波分解中，由于仅仅采用一种结构元素进行运算，使得滤波和特征频率向量的提取能力均未达到最优。

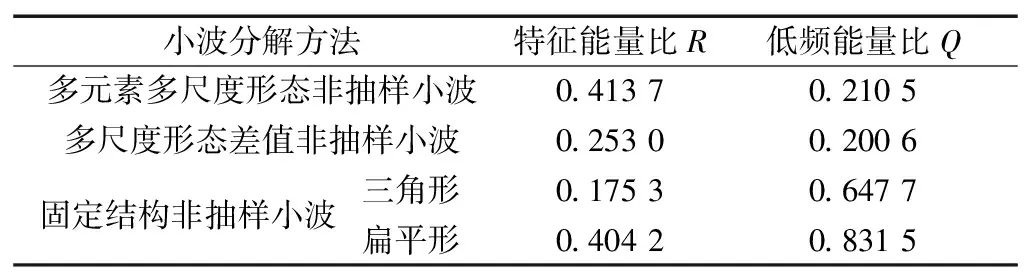
表2 模拟试验效果对比

3 试验验证

为验证多元素多尺度非抽样小波变换方法的有效性，选用轴承内圈、外圈2种故障状态进行分析。实测轴承振动加速度数据来自Case Western Reserve University(CWRU)轴承数据中心网站。轴承局部损伤由电火花机加工，直径为0.177 8 mm，转速为1 797 r/min，转频为29.95 Hz，轴承外圈和内圈故障的特征频率分别为107.8 Hz和159.6 Hz。试验信号采样频率为12 kHz，采样点数为6 000。轴承外圈和内圈故障信号时域波形如图6所示。

图6 滚动轴承故障信号时域波形

基于多元素多尺度形态非抽样小波分别对2种故障状态下的轴承振动加速度信号进行分解，并求取第2层近似信号的频谱。分解过程中，三角形结构元素g0={0 2 4 2 0}；扁平形结构元素g1={0 0 0 0 0}。

轴承外圈故障信号的分解时域图和第2层近似信号频谱图分别如图7和图8所示，可以看出，经由多元素多尺度形态非抽样小波分解，外圈故障特征频率及其倍频可以清晰地得到，且特征能量比R达到0.633 5。

选用同样结构元素对轴承内圈故障信号进行分析处理，结果如图9和图10所示。可以看出，轴承内圈故障特征频率及其1，2倍频被清晰地提取，且其特征能量比R=0.476 8。由此可见，多元素多尺度非抽样小波变换可以清晰地提取出轴承的内、外圈故障，且信噪比较高，效果较好。

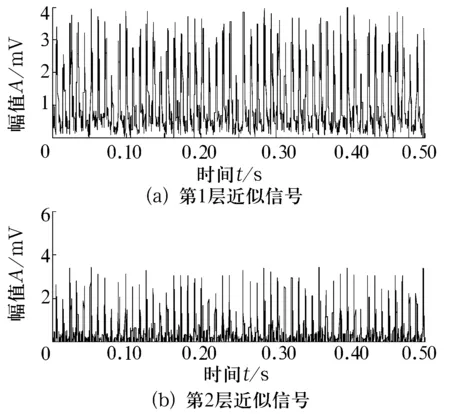
图7 外圈故障信号分解时域图

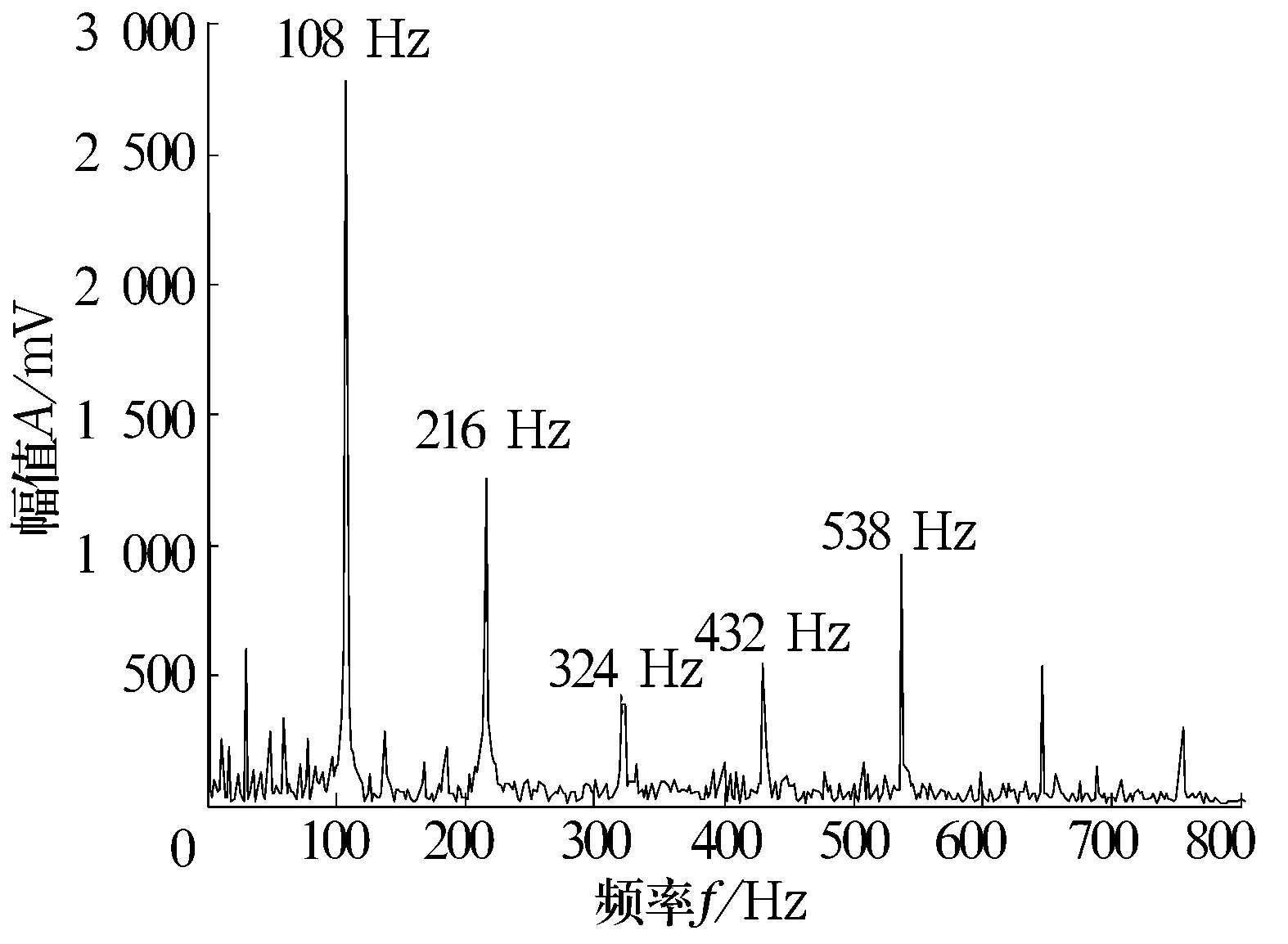
图8 外圈第2层近似信号频谱图

图9 内圈故障信号分解时域图

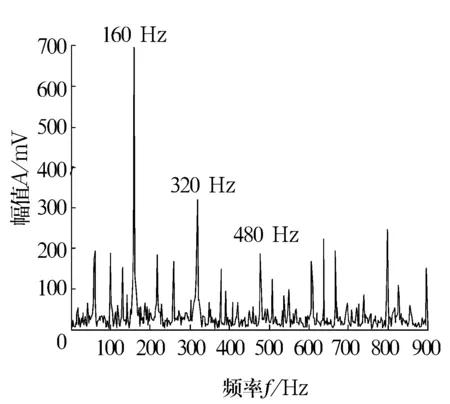
图10 内圈第2层近似信号频谱图

4 结束语

多元素多尺度形态非抽样小波分解方法考虑了不同的形态学结构元素对于滤波和冲击频率提取的影响，在形态学小波分解过程中采用不同的结构元素，与现有的形态非抽样小波分解方法相比，该方法既能够有效地提取故障特征频率信息，又有很好的滤波效果。