一种关于函数之间关系的函数与究极关系

何姜林

（成都大学城乡建设学院,四川成都610106）

一种关于函数之间关系的函数与究极关系

何姜林

（成都大学城乡建设学院,四川成都610106）

定义了一种新的关系“究极关系”,通过“究极关系”找到了判断函数大小关系和复杂函数求导的一般方法,通过这种求导的方法求切线斜率变得非常简单,并讨论了函数之间的一些微妙性质.由究极关系得到了一种新的函数形式（分部变化函数）,并初步讨论了这种函数的积分.

究极关系；求导关系；分部变化函数；积分；函数关系

以前的数学工作者研究一个函数,研究的是这个函数中变量对这个函数整体的效果,而如今数学的发展是研究函数自身,我们必须了解一个函数的结构是怎么影响这个整体的[1-3]；按照以往的研究思路很难具体地了解函数本身的内部结构对于这个整体的影响,对函数的研究很难突破这个瓶颈[4],迫切地寻求一种新的思路、一种新的工具来研究函数[5-6].

本文把一个函数分成多个部分来研究.受方程中设未知数的思想的影响,以全新的定义实现了对于在多个函数之间建立未知关系即“究极关系”的方法,并根据“究极关系”把任意一个函数分为多个部分,进而得到了全新的求导方法：分部分求导再相加.简化了求导的运算,打破了求切线斜率时,坐标不可在求导过程中代入运算的思想,极大的简化了求切线的斜率的方法.并根据究极关系的一些固有性质讨论了函数的一些性质.

1 究极关系定义

在比较a与b的大小的过程中,经过化简最终是可以确定a与b的大小关系的,但是在化简之前是不确定的,这类似于解方程中的未知数x,于是不妨也设a与b的大小关系为未知关系,然后利用关系运算法则来最终确定.

定义1设“○x”表示一种不等关系,如“○x ”可以表示“＞”“＜”“=”.

设f（x）为定义域A内单调函数,且a∈A,b∈A；当f（x）为单调函数时f（a）与f（b）的大小同a与b相同,当f（x）为减函数时,f（a）与f（b）的大小与a与b相反.例如,相同关系：a＞b则f（a）＞f（b）；相反关系：a＜b则f（a）＜f（b）.“=”的相反关系仍然是“=”.

不等关系是可以传递的,如,a＞b,b＞c则a＞c.

在F（x）=g（x）+f（x）中F（x）是由g（x）与f（x）两部分在“+”这种关系下组成的,由此可以联想到一个函数是G（x）由n个函数经过一定的关系联合组成的,把G（x）叫做这n个函数的集函数,把这n个函数叫做G（x）的分函数.有n个究极关系式就有n+1个分函数（注：分函数之间可以有相同的函数）.

g(x)

iv同一个式子可以经过不同的关系来表示；

vi函数G（x）中x的必须全部分配到分函数中.

可以这样理解函数中的究极关系,即设一个时钟是由指针、机械螺母、电池3部分合理连接、协调工作组成了时钟这样一个整体；这3部分的连接关系就相当于函数中的究极关系.

2 函数的关系

判断：（用反证法）假设f( x)≠m( x),设a为任意一个常数,令a=x则有F( a)=f( a)—x—→ g( a)=m(a)—x—→ g( a)；

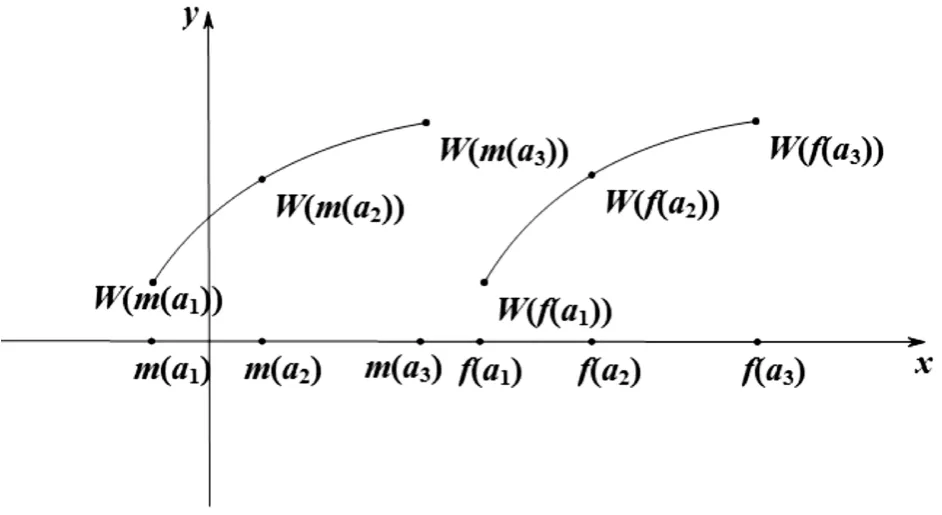
图1 两个函数的分部情况Fig.1 Case of two functions

由图1可以看出在这种情况下当W( x)在[m(a3),f(a1)]之间存在单减情况时假设成立.如,,其中f( x)=x, g( x)=3,当m( x)=x+2π时,成立.

定理1x 设F(x)为定义域内的单调函数,当存在有等式g( x)和F( x)=m( x)——→g( x),则必有f( x)=m( x)恒成立.

推论（唯一确定性定理）1设F(x)为定义域内的单调函数,存在有下面两个等式和,则必有恒成立.

那么必有

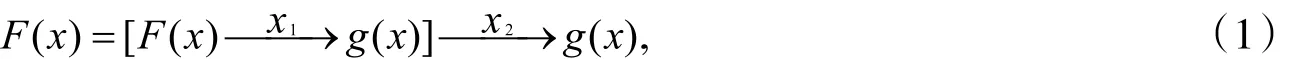
把y(x)叫做中介函数.

定理2对任意一个函数F(x)可以有任意多个任意分函数.

证明：由式（1）有

其中

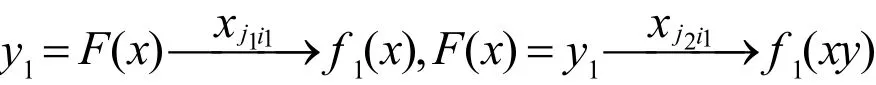
同理有

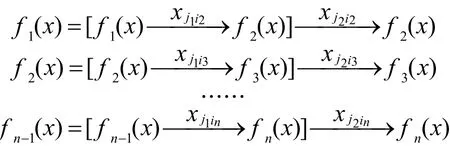
推论2对任意一个函数F(x)可以有任意多个任意的完整的或不完整的分函数.

3 究极关系下的求导公式

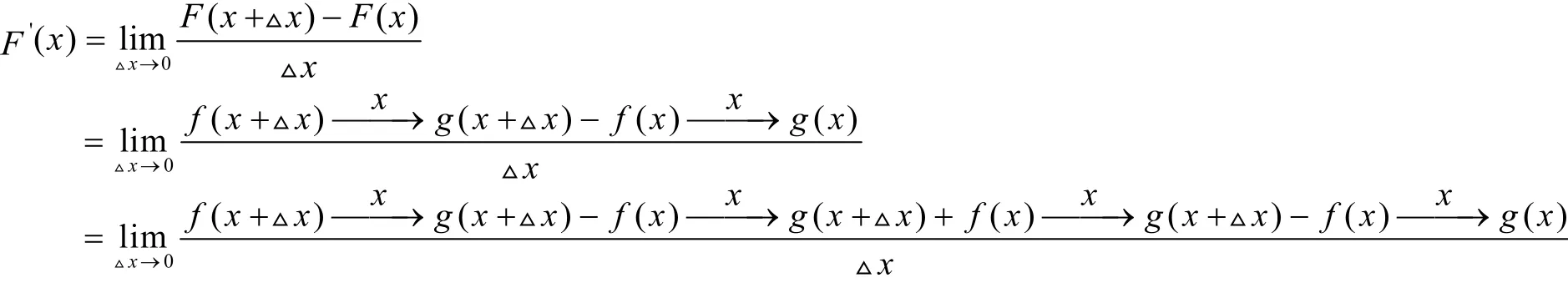
令g( x)=a, f( x)=b ,则

设F'(x)=m( x, a, b),m( x, a, b)为求导最后结果,再把b、a分别用f( x)、g( x)带入m( x, a, b)即得结果.其中a、b并不参与变量的求导,称b、a为函数f( x)、g( x)的常数表达形式.

证明：设F（x）函数的常数表达式为f( x)=a、g( x)=b,根据式（2）有

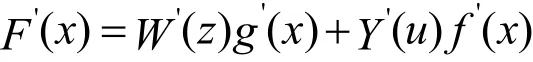
即得

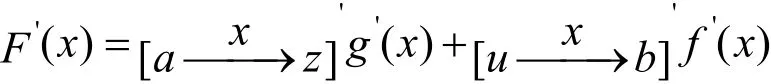
上面是把一个函数化为两个函数表示时的求导方法,那么当把一个函数化为三个或则更多个函数表示时的求导方法为,设

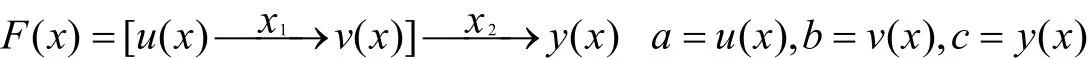
则有

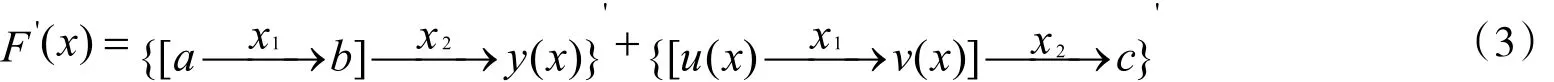
令

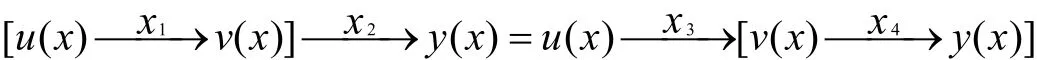
代入式（3）,有

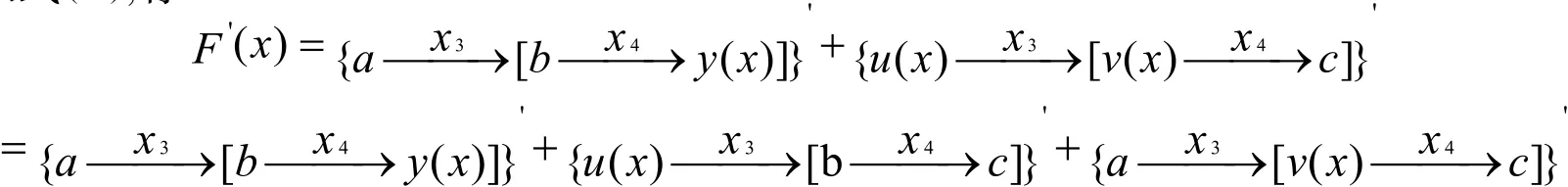
令

代入则有

同理,令

那么就有

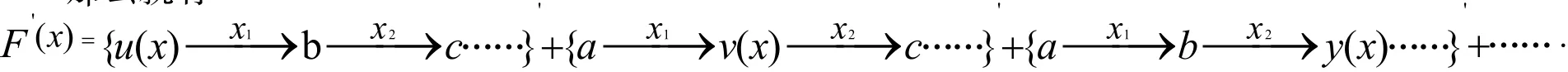
上述只考虑的函数之间构成的是完整关系,根据式（2）易知对于不完整关系也成立.

由上可以看出求导的过程是先对一部分变量进行求导,再对另一部分求导,最后两部分结果相加得到的过程.

解：令1-x=a,1+x=b ,根据（2）则

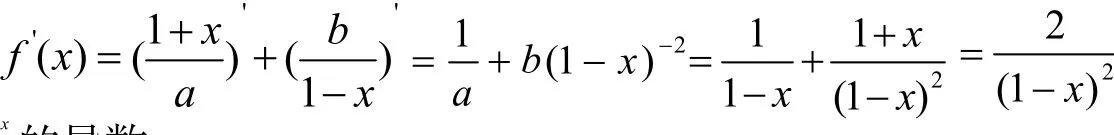
例二：求f( x)=xxx的导数.

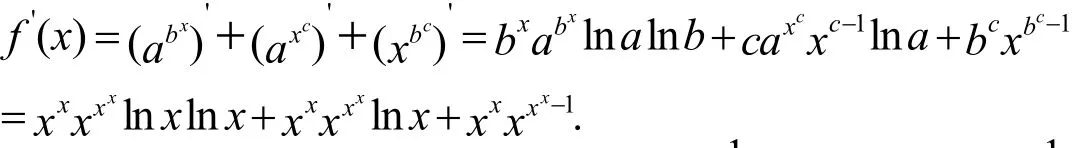
另一解法：两边同取对数lnf( x)=xxlnx,两边求导；令y=xx,则lny=xln x；

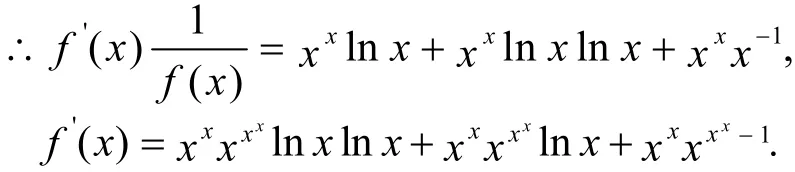
定理3设F（x）、g（x）为定义域内的连续可导函数,则有

其中b=g( x), c=F( x)；F( x)=f( x)g( x),f( x)=F( x)g( x),f( x)为中介函数.

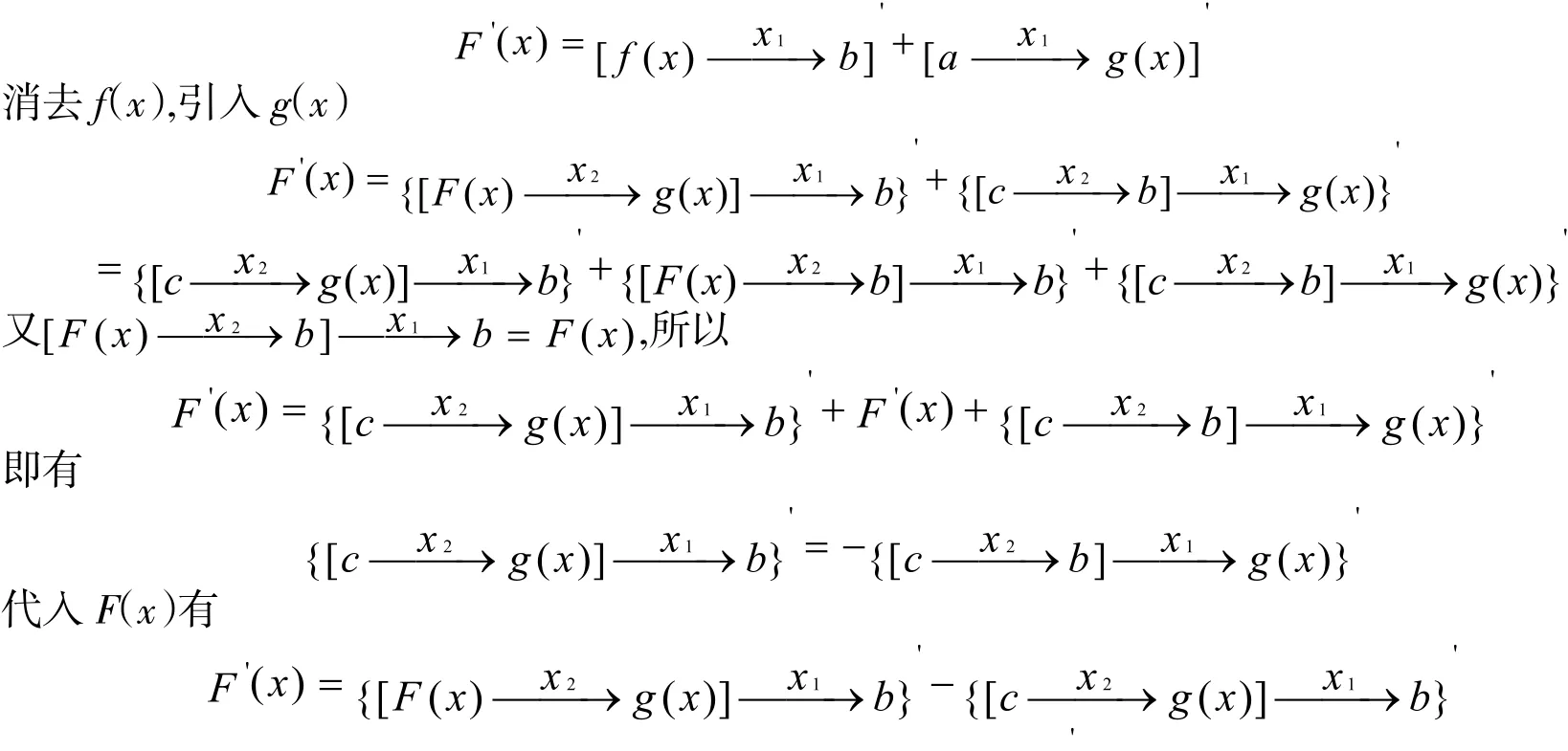
为了方便讨论把g（x）中的自变量标记为j,F（x）中的自变量标记为x.

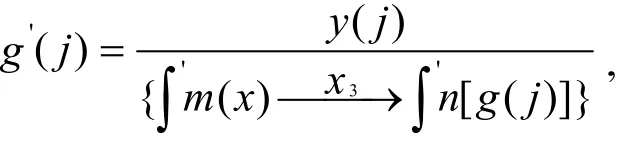
得W'[g( x)]=y( j ),因为g（x）并不唯一所以y（j）也不唯一,即

的值并不唯一,得证.

4 究极关系下的斜率与积分

4.1 过点（x0,y0）的切线斜率

设（fx）过点A（x0,y0）,且,求在点A的斜率.

解：令a=u( x), b=v( x),则

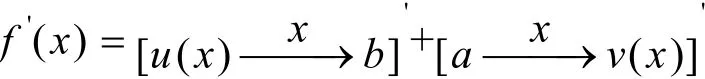
求出f'(x),再令x=x0则得（fx）在点A的斜率

例一：求y=x ln x在x=1处的导数.

解：在x=1处有

例二：求y=(1+x2)tanx在x=0的导数.

4.2 分部变化函数及其积分

设f'(x)=g(x)+g(x),其中g(x) =[y(x)—x— →y( x)]'；令

121120

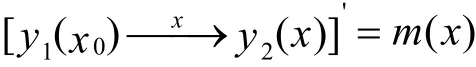
则有

所以有

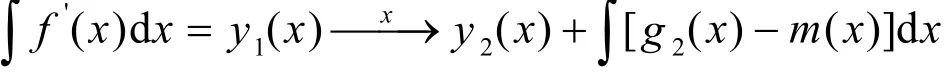
定义4把这种为了满足特定的情况通过控制变量的变化而把一部分变量暂时当作常量进行求导的函数叫做分部变化函数.

F（x,x0）为f（x,x0）的一个原函数,称（4.1）为广义积分公式,当x0=0时即为传统求积公式.根据广义积分公式易知有

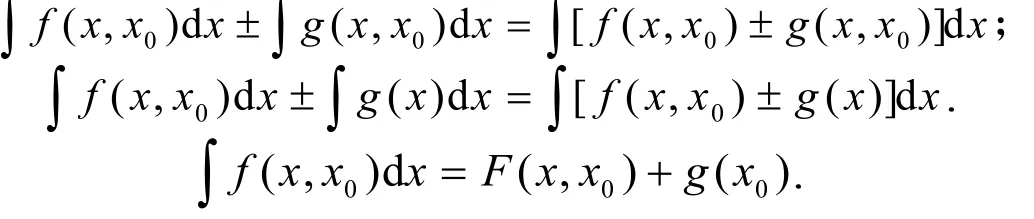
已知∫kf( x, x0)dx=k∫f( x, x0)d x ,设G（x）为（fx,x）的一个原函数,令

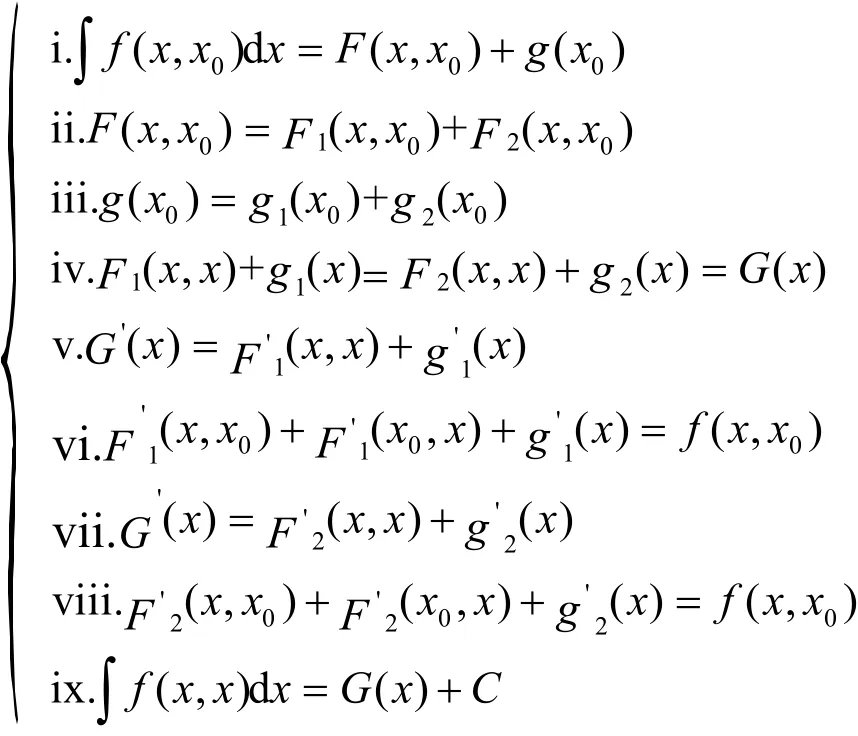
根据此方程组中的某些方程即可解出G（x）,对于方程vi和viii要是最后不能将方程中的x0消去,则方程vi和viii就等价于方程v和vii；以后对分部变化函数的研究也得依据此方程组.

5 小结

本文引入究极关系是为了研究函数与函数之间的关系,以及函数在某一关系下所具有的性质.通过究极关系可以研究系统与系统间的连接方式,根据系统的连接方式来确定部分系统和求得系统的性质.讨论了究极关系对求导的帮助,通过对究极关系的研究将对分部变化函数、微分方程以及极限的研究开启一种新的思路；更是将函数与函数之间的研究抽象到关系与关系的研究.今后对用怎样的组合关系对函数的研究更方便,及函数（或系统）之间的组合方式和究极关系在多元函数中的性质还需进一步研究.

[1]Hardy G H.纯数学教程[M].北京：人民邮电出版社,2011.

[2]北京大学哲学系外国哲学史教研室.西方哲学原著选读[M].北京：商务印书馆,1982.

[3]华东师范大学数学系.数学分析,上册[M].3版.北京：高等教育出版社,2001：101.

[4]甘欣荣,汤光送.幂指函数性质的推广[J].甘肃联合大学学报：自然科学版,2011,25（2）：26-28.

[5]Wu T,Biswas S.Minimizing inter-cluster interference by self-reorganizing MAC allocation in sen,networks[J].Wireless Networks, 2007,13（5）：691-703.

[6]卢亚丽,李艳华,李战国,等.变限积分函数求导方法研究[J].河南教育学院学报：自然科学版,2004,13（1）：4-6.

（责任编辑：卢奇）

A new function about relationship between functions and Ultimate Relationship

He Jianglin
（College of Urban and Rural Construction,Chengdu University,Chengdu 610106,China）

The definition of Ultimate Relationship and through Ultimate Relationship find judging function size and the derivation method of complex function,through this derivation method makes the slope of the tangent line method becomes very simple.The Ultimate Relationship is a new form of function（Segment varying function）,and discusses the function of integral.

Ultimate Relationship；the derivation relation；segment varying function；Integration；functional relation.

O174.6

A

：1008-7516（2014）01-0049-07

10.3969/j.issn.1008-7516.2014.01.010

2013-11-14

成都大学创新性实验资助（CDUCX201301028）

何姜林（1992-）,男,四川雅安人.主要从事数理逻辑、分析哲学研究.