基于区间粗糙数互补判断矩阵的一种排序方法

谢凤平,曾雪兰,段云艳

(广西大学 a.数学与信息科学学院;b.电气工程学院,南宁 530004)



基于区间粗糙数互补判断矩阵的一种排序方法

谢凤平a,曾雪兰a,段云艳b

(广西大学 a.数学与信息科学学院;b.电气工程学院,南宁 530004)

定义了区间粗糙数互补判断矩阵和正态分布区间粗糙数,并给出区间粗糙数互补和互反判断矩阵的相互转化公式.针对基于区间粗糙数互补判断矩阵的排序问题,提出了一种基于可能度的区间粗糙数互补判断矩阵的排序方法.通过对方案进行两两比较,构造区间粗糙数互补判断矩阵,求解出形式为区间粗糙数的权重向量,利用可能度公式得到权重向量的可能度矩阵,从而得到各方案的排序.实例分析说明了该方法的实用性和有效性.

区间粗糙数;正态分布;可能度;互补判断矩阵;排序

0 引言

20世纪70年代初,Saaty教授提出一种将定性与定量相结合的决策方法——AHP[1],现已被广泛运用到环境评估、投资决策、交通改善以及经济效益综合评价等诸多方面.判断矩阵是层次分析法的核心内容之一.常见的判断矩阵有两类：互补判断矩阵和互反判断矩阵.在实际应用中,判断矩阵元素的形式主要以实数[2]、区间数[3-4]、模糊数[5-7]等形式给出.有时判断矩阵元素也可以是区间粗糙数的.区间粗糙数是经典粗糙集的一个拓展,它比区间数、模糊数、语言值等能更好地刻画事物不确定性.目前,对区间粗糙数的研究比较少,文献[8-9] 研究了区间粗糙数的定义和一些基本性质,而后相关学者也进行了一些补充、拓展,但仍存在很多有待完善之处.针对属性值为区间粗糙数的多属性决策问题,文[10]根据离差最大化思想给出了一类区间粗糙数的多属性决策方法.文献[11]和文献[12]分别提出带有偏好的和基于可能度的区间粗糙数多属性决策方法.文献[13]给出了一种基于WIRDAA算子解决了准则值为区间粗糙数随机变量的多准则决策问题.迄今为止,尚未见对区间粗糙数判断矩阵的研究.

在利用AHP解决决策问题时,专家给出的判断结果可以是区间粗糙数的形式.例如,某专家判断方案xi与方案xj的重要程度比为一个区间粗糙数([0.3，0.4],[0.2,0.5])表示方案xi比方案xj重要程度在0.3到0.4之间是肯定的,在0.2到0.5之间是可能的.因此,解决基于区间粗糙数判断矩阵的排序问题具有重要的理论意义和实际应用价值.为此,本文将AHP中的判断矩阵的元素形式推广到区间粗糙数.通过对方案进行两两比较,构造互补区间粗糙数判断矩阵,给出了基于正态分布区间粗糙数的可能度,提出了一种基于区间粗糙数互补判断矩阵的排序方法,也给出了区间粗糙数互补判断矩阵和区间粗糙数互反判断矩阵的相互转化公式.最后给出算例说明该方法是可行的,且具有一定实用价值.

1 区间粗糙数基本概念

定义1[14]设论域U和概念的集合X,则定义其下近似和上近似分别为：

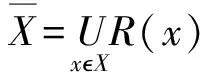
其中R(x)={yU|y≅x},R-1(x)={yU|x≅y}(≅表示满足自反性,但不满足对称性和传递性的一种二元相似关系).

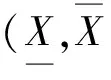
定义3[10]下近似和上近似均为区间的粗糙集称为区间粗糙数,记为([a,b],[c,d])其中c≤a≤b≤d.

定义4[11]设ξ=([a,b],[c,d]),ξ1=([a1,b1],[c1,d1]),ξ2=([a2,b2],[c2,d2]),均为区间粗糙数,其中c,c1,c2≥0,λ>0为实数,则有:

1)ξ1+ξ2=([a1+a2,b1+b2]),([c1+c2，d1+d2]);

2)ξ1·ξ2=([a1a2,b1b2]),([c1c2，d1d2]);

3)ξλ=([aλ,bλ],[cλ,dλ]).

定义5 设ξ=([a,b],[c,d]),ξ1=([a1,b1],[c1,d1]),ξ2=([a2,b2],[c2,d2])均为区间粗糙数,其中c,c1,c2≥0,则有：

1)ξ-1=([b-1,a-1],[d-1,c-1]);

2 可能度公式及性质

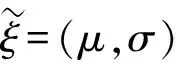
(1)

(2)

由定义6可知,正态分布区间数实质表示一个均值和方差满足(1)(2)条件的正态分布区间数,由文献[16]可得区间粗糙数的可能度公式如下.

定义7 设区间粗糙数ξ1=([a1,b1],[c1,d1]),ξ2=([a2,b2],[c2,d2]),则称

(3)

为ξ1≥ξ2的可能度,其中μ1,μ2,σ1,σ2由定义6给出.查表即可求出p(ξ1≥ξ2).

显然,可能度有以下性质：

性质1 设ξ1=([a1,b1],[c1,d1]),ξ2=([a2,b2]),[c2,d2]),ξ3=([a3,b3],[c3,d3])均为区间粗糙数,其中c1,c2,c3≥0,则

1)(有界性)0≤P(ξ1≥ξ2)≤1;

2)(互补性)P(ξ1≥ξ2)+P(ξ2≥ξ1)=1;

3 两类区间粗糙数判断矩阵及其相互转化公式

定义8 设判断矩阵η=(ηij)n×n,其中ηij=([aij,bij],[cij,dij])且0≤cij≤aij≤bij≤dij,若aij+bji=bij+aji=cij+dji=dij+cji=1,aii=bii=cii=dii=0.5(i,j=1,2,…n)则称矩阵η是区间粗糙数互补判断矩阵.

定义9 设判断矩阵ξ=(ξij)n×n,其中ξij=([mij,nij],[lij,kij])且0≤lij≤mij≤nij≤kij,若mij·nji=nij·mji=lij·mji=lij·kji=kij·lji=1,则称矩阵ξ是区间粗糙数互反判断矩阵.

定理1 设区间粗糙数互补矩阵η=(ηij)n×n,ηij=([aij,bij],[cij,dij]),0≤cij≤aij≤bij≤dij,则通过转化公式

ξij=ηij/ηji

(4)

可得到区间粗糙数互反矩阵ξ=(ξij)n×n.

证明 令ξij=([mij,nij],[lij,kij]),则有

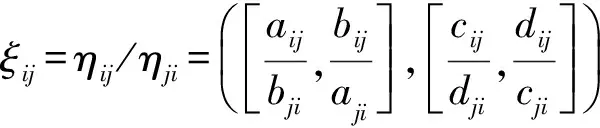
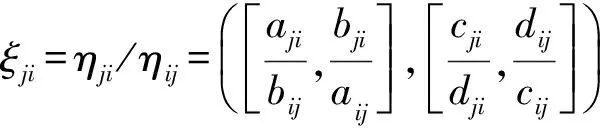
同理易证nij·mji=lij·kji=kij·lji=1.所以矩阵ξ=(ξij)n×n是区间粗糙数互反判断矩阵.

定理2 设区间粗糙数互反判断矩阵ξ=(ξij)n×n,其中ξij=([mij,nij],[lij,kij]),且mij·nji=nij·mji=lij·kji=kij·lji=1,0≤lij≤mij≤nij≤kij,则通过转化公式：

(5)

则η=(ηij)n×n是区间粗糙数互补判断矩阵.

证明 由题意可知

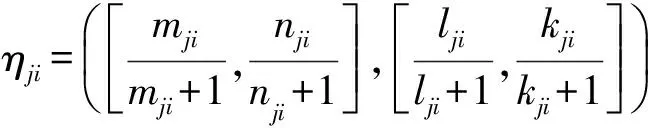
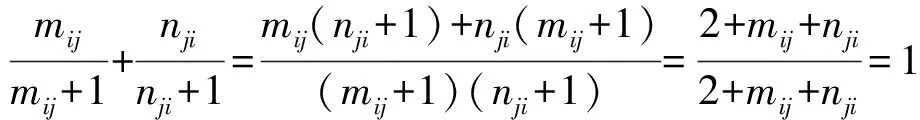
同理可证

故η=(ηij)n×n是区间粗糙数互补判断矩阵.

由上可知,区间粗糙数互补判断矩阵和区间粗糙数互反判断矩阵可以通过转化公式相互转化.因此,本文仅考虑区间粗糙数互补判断矩阵的排序问题.

4 区间粗糙数互补判断矩阵的排序方法

在某决策问题中,假设有n个备选方案μ1,μ2，…，μn,在0.1～0.9标度,决策者对决策方案进行两两比较,得到形式为区间粗糙的互补判断矩阵ξ=(ξij)n×n,其中ξij=([aij,bij],[cij,dij])且0≤cij≤aij≤bij≤dij,aij+bji=bij+aji=cij+dji=dij+cji=1,aii=bii=cii=dii=0.5,i,j.1,2,…，n.

排序方法具体步骤如下：

步骤1 利用行和并归一化,求得形式为区间粗糙数权重w=(w1,w2,w3,…，wn),其中

(6)

步骤2 由定义6可得正态分布区间粗糙数权重向量

wi=(μi,σi) ;

步骤3 利用公式(3)建立权重可能度矩阵

其中pij=p(wi≥wj);

5 算例分析

某企业计划投资某项目,拟定4个备选方案μi(i=1,2,3,4).决策者将决策方案进行两两比较,给出形式为区间粗糙数的互补判断矩阵ξ,如下：

1)由公式(4)求得区间粗糙矩阵权重w=(w1,w2,w3,w4),即

w=(([0.23,0.38],[0.16,0.53]),([0.15,0.32],[0.13,0.39]),([0.21,0.30],[0.14,0.49]),([0.16,0.32],[0.08,0.49])).

2)由定义6可得

w1=(0.305,0.048),w2=(0.235,0.035),w3=(0.255,0.038),w4=(0.24,0.053).

3)由公式(3)查表得到可能度矩阵

v=(0.167,0.297,0.255,0.281).

5) 由上可得v1

6 结论

本文首次提出区间粗糙数形式的判断矩阵,并给出正态分布区间粗糙数及其可能度的定义,将AHP的判断矩阵形式推广到区间粗糙数形式,进一步完善了AHP理论基础,有效解决了判断矩阵的元素为区间粗糙数的决策问题.该方法可以用于供应商选择、投资决策、项目评估以及经济效益综合评价等相关决策方面.

[1]Saaty T L.The Analytic Hierarchy Process[M].New York: McGraw-Hill,1980.

[2]徐泽水.部分权重信息下对方案有偏好的多属性决策法[J].控制与决策,2004,19(1):71-75.

[3]徐泽水.区间数互补判断矩阵排序的一种实用方法[J].运筹与管理,2001,10(1):16-19.

[4]徐改丽,谢晓兰.区间数互补判断矩阵的一致性及排序方法的研究[J].模糊系统与数学,2013,27(2):162-168.

[5]徐泽水.模糊互补判断矩阵排序的一种算法[J].系统工程学报,2001,16(4):311-314.

[6]肖钰,李华.基于三角模糊数的判断矩阵的改进及其应用[J].模糊系统与数学,2003,17(2):59-64.

[7]徐泽水.三角模糊数互补判断矩阵排序方法研究[J].系统工程学报,2004,19 (1):85-88.

[8]Liu B. Theory and practice of uncertain programming [M].Heidelberg: Physica Verlage, 2002.

[9]Liu B. Uncertain theory: An introduction to its axiomatic foundation [M].Berlin: Springer Verlag,2004.

[10]曾玲,曾祥艳. 一类区间粗糙数多属性决策方法研究[J].控制与决策,2010, 25(11):1757-1760.

[11]曾智,钱伟懿,赵芳芳.对方案有偏好的区间粗糙数多属性决策方法[J].渤海大学学报(自然科学版),2012,33(2): 101-105.

[12]钱伟懿,曾智. 基于可能度的区间粗糙数排序方法[J].运筹与管理,2013,22(1):71-76.

[13]王坚强,唐平.基于区间粗糙算子的粗糙随机多准则决策方法[J].控制与决策,2011,26(7):1056-1059.

[14]Slowinski R,Vanderpooten D.A generalized definition of rough approximations Based on similarity[J].IEEE Trans on knowledge and Engineering,2000,12(2):331-336.

[15]Pawlak Z. Rough sets[J].International Journal of Computer and Information Sciences,1982,11(5):341-356.

[16]徐改丽,吕跃进.基于正态分布区间数的多属决策方法 [J].系统工程学报,2011,29(9):120-123.

Priority Method for Complementary Judgement Matrix Based on Interval Rough Number

XIE Feng-pinga,ZENG Xue-lana,DUAN Yun-yanb

(a. School of Mathematics and Information Sciences, b. School of Electrical Engineering,Guangxi University,Nanning， 530004,China )

The definitions of interval rough number complementary judgement matrix and distribution interval rough number are given, and the mutual transformation formula between interval rough number complementary judgement matrix and interval rough number reciprocal judgement matrix is set up as well. For the priority problem based on interval rough number complementary judgment matrix, a ranking method of interval rough number complementary judgement matrix based on possibility degrees is proposed. Interval rough number complementary judgement matrix is constructed by pair comparison. Then, the weight vectors with forming of interval rough number are worked out. By using the formula of possibility degrees, the possibility degree matrix of weight vector is established, and according to the ordering formula, and the ranking of alternatives is obtained. Finally, a numerical example is given to show the effectiveness and feasibility of this approach.

interval rough number; normal distribution; possibility degree; complementary judgement matrix; priority.

2015-05-03

国家自然科学基金资助项目(71361002);广西自然科学基金资助项目(2013GXNSFAA019016)

谢凤平(1987-),女,湖南邵阳人,广西大学数学与信息科学学院 13级应用数学专业硕士研究生,研究方向为决策分析及粗糙集.

曾雪兰(1962-),女,广西贺州人， 广西大学数学与信息科学学教授, 研究方向为管理决策分析理论与方法研究.

C934

A

1008-6722(2015) 05-0022-05

10.13307/j.issn.1008-6722．2015．05．06