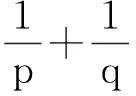AnoteontheBohrinequalityinC*-algebras

,

(1.Department of Mathematics and Statistics, Yulin University, Yulin 719000, Shaanxi, China;2.Department of Mathematics, Huizhou University, Huizhou 516007, Guangdong,China)



AnoteontheBohrinequalityinC*-algebras

ZHANGQiaowei1,LIWenbo2

(1.DepartmentofMathematicsandStatistics,YulinUniversity,Yulin719000,Shaanxi,China;2.DepartmentofMathematics,HuizhouUniversity,Huizhou516007,Guangdong,China)

Abstract:By using an isometric *-representation from a C*-algebra into B(H), where H is a Hilbert space,the generalized Bohr inequalities in a C*-algebra were discussed.Some necessary and sufficient conditions for four generalized Bohr inequalities are obtained. The main results are as follows:Let p,q∈R+ and 1/p+1/q=1, then for all A,B∈S(S is a unital C*-algebras),|A-B|2+|(1-p)A-B|2≤p|A|2+q|B|2 iff p≤2. Let α,β,u,v∈R+ and p,q∈C+, then for all A,B∈S,|αA+βB|2+|uA+vB|2≤p|A|2+q|B|2 iff p≥α2+u2,q≥β2+v2 and (p-(α2+u2))(q-(β2+v2))≥(αβ+uv)2..

Key words:Bohr inequality; C*-algebra; *-representation

0Introduction

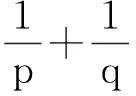
|a-b|2≤p|a|2+q|b|2

(1)

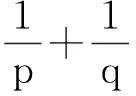
‖v+w‖2≤p‖v‖2+q‖w‖2.

In2003,Hirzallah[2]furthergeneralizedtheinequalitytothecontextofoperatoralgebras.

AnoperatorversionoftheBohrinequalitywasobtainedbyHirzallah[2].

|A-B|2+|(1-p)A-B|2≤p|A|2+q|B|2.

(2)

Itisworthwhilenotingthatinreference[2],onlythesituationwhereq≥p>1isconsidered.Equivalently,theconjugateexponentsp,qareonlyrestrictedtoq≤2and1

Recently,reference[4]provedsomerelatedoperatorinequalitiesbymeansof2×2 (block)operatormatrices,andnallygivedageneralizationoftheoperatorBohrinequalityformultipleoperators.Someveryinterestingoperatoridentitieswerealsoestablished.

(3)

Byusingtheidentity(3),theinequality(2)deducedtheconditionthatp≤qinreference[4].

In2010,reference[10]generalizedtheclassicalBohrinequalityfromHilbertspaceoperatorstothecontextofC*-algebrasandsomeextensionsandrelatedinequalitieswereobtained.Foreachinequality,thenecessaryandsuffcientconditionfortheequalitywasalsoobtained.

Inthisnote,byusinganisometric*-representationbetweenC*-algebraandB(H),whereHisaHilbertspace,wegivesomenecessaryandsufficientconditionsforfourgeneralizedBohrinequalitiesinC*-algebras.

1Mainresults

LetSbeaunitalC*-algebrawithaunitI.ForallA∈S,put|A|=(A*A)1/2.

(a)ForallA,B∈S,

|A-B|2+|(1-p)A-B|2≤p|A|2+q|B|2.

(4)

(b) p≤2.

ProofLet(a)hold,andA=I,B=0in(4),thenwehave(p-2)(p-1)=p2-3p+2≤0.Sincep>1,weseethatp≤2.

Let(b)hold.Thenp≤q.Toprove(a),i.e.forallA,B∈S, (4)holds.LetΦ:S→B(H)beanisometric*-representationofS.ByTheorem1,wehave

|Φ(A)-Φ(B)|2+|(1-p)Φ(A)-Φ(B)|2≤p|Φ(A)|2+q|Φ(B)|2,A,B∈S.

SinceΦisanisometricisomorphismofS,wehave|Φ(X)|=Φ(|X|)forallX∈S.Hence,

and

p|Φ(A)|2+q|Φ(B)|2=Φ(p|A|2+q|B|2).

This shows that

Φ(|A-B|2+|(1-p)A-B|2)≤Φ(p|A|2+q|B|2).

From the fact thatΦ(X)≤Φ(Y)⟺X⟺Y, we see

|A-B|2+|(1-p)A-B|2≤p|A|2+q|B|2.

for allA,B∈S. This theorem is proved.

Lemma 1Letl,m∈R. Thenlx2+my2≥2xyholds for allx,y∈R， if and only ifl>0,m>0 andlm≥1.

ProofPutf(x,y)=lx2+my2-2xy. Suppose thatf(x,y)≥0 for allx,y∈R.Thenl=f(1,0)≥0,m=f(0,1)≥0.Clearly, lm≠0.Thus, m>0andl>0.Since

weseethatlm≥1.

Conversely,weassumethatl>0,m>0andlm≥1.Thenforallx,y∈R,wehave

Thislemmaisproved.

Theorem 4Letα,β,u，v∈R be real numbers andp,q∈R+be positive real numbers. Then the following statements are equivalent.

(a) For allA,B∈S,

|αA+βB|2+|uA+vB|2≤p|A|2+q|B|2.

(5)

(b)p≥α2+u2,q≥β2+v2and

(p-(α2+u2))(q-(β2+v2))≥(αβ+uv)2.

(6)

ProofLet (a) hold. Then for all real numbersx,y, takingA=xI,B=yIin (5) yields that

(αx+βy)2+(ux+vy)2≤px2+qy2,

that is

[p-(α2+u2)]x2+[q-(β2+v2)]y2≥2(αβ+uv)xy.

(7)

Takingx=1,y=0 andx=0,y=1 in (7) respectively, we getp≥α2+u2andq≥β2+v2. Thus, in the case whereαβ+uv=0, the inequality (6) is clearly valid.

Hence, we may assume thatαβ+uv>0. Therefore, (7) implies that

[p-(α2+u2)](αβ+uv)-1x2+[q-(β2+v2)](αβ+uv)-1y2≥2xy,

for allx,y∈R. Lemma 1 shows that

[p-(α2+u2)](αβ+uv)-1·[q-(β2+v2)](αβ+uv)-1≥1,

which is as same as (6).

Let (b) hold andΦ:S→B(H) be an isometric*-representation ofS. By Theorem 6 of reference[3], we have

|αΦ(A)+βΦ(B)|2+|uΦ(A)+vΦ(B)|2=p|Φ(A)|2+q|Φ(B)|2.

SinceΦis an isometric isomorphism ofS, on the C*-algebraΦ(S), we have |Φ(X)|=Φ(|X|) for allX∈S. Hence,

and

p|Φ(A)|2+q|Φ(B)|2=Φ(p|A|2+q|B|2).

This shows that

Φ(|αA+βB|2+|uA+vB|2)≤Φ(p|A|2+q|B|2).

From the fact thatΦ(X)≤Φ(Y)⟺X⟺Y, we see

|αA+βB|2+|uA+vB|2≤p|A|2+q|B|2,

for allA,B∈S. This theorem is proved.

Theorem 5Leta,b∈R+be positive real numbers andc∈C. Then the following statements are equivalent.

(b) For allA,B∈S,

(8)

(b)ab≥|c|2.

ProofLet (a) hold andc≠0.Writec=|c|exp(iθ) and for allx,y∈R,using (8) forA=exp(iθ)xIandB=-yIyieds that

ax2+by2≥2|c|xy.

Hence, Lemma 1 yields thatab≥|c|2.

Let (b) hold andΦ:S→B(H) be an isometric *-representation ofS. Writec=|c|exp(iθ), then by using Lemma 1 of reference [3] for exp(-iθ)Φ(A) andΦ(B), we have

a|exp(-iθ)Φ(A)|2+b|Φ(B)|2+|c|(exp(iθ)Φ(A)*Φ(B)+exp(-iθ)Φ(B)*Φ(A))≥0.

Thus,

a|exp(-iθ)Φ(A)|2+b|Φ(B)|2+|c|(exp(iθ)Φ(A)*Φ(B)+exp(-iθ)Φ(B)*Φ(A))=

Φ(a|exp(-iθ)A|2+b|B|2+|c|(exp(iθ)A*B+exp(-iθ)B*A))≥0.

From the fact thatΦ(X)≥0⟺X≥0, we see that (8) holds. This theorem is proved.

Theorem 6Letα,β∈R andx,y∈R+be positive numbers. Then the following statements are equivalent.

(a) For allA,B∈S,

|αA+βB|2≤x|A|2+y|B|2.

(9)

(b)x≥α2,y≥β2and (x-α2)(y-β2)≥α2β2.

ProofLet (a) hold. Using (8) forA=I,B=0 andA=0,B=Irespectively, we havex≥α2,y≥β2. For all real numberss,t, lettingA=sIandB=tIin (9) yields that

(x-α2)s2+(y-β2)t2≥2αβst.

Clearly, we may assume thatαβ>0. Thus, Lemma 1 implies that (x-α2)(y-β2)≥α2β2.

Conversely, letΦ:S→B(H) be an isometric *-representation ofS. Then from reference [4] we can see that for allA,B∈S,

|αΦ(A)+βΦ(B)|2≤x|Φ(A)|2+y|Φ(B)|2.

This shows that

Φ(|αA+βB|2)≤Φ(x|A|2+y|B|2).

From the fact thatΦ(X)≤Φ(Y)⟺X⟺Y, we see

|αA+βB|2≤x|A|2+y|B|2,∀A,B∈S.

This theorem is proved.

参考文献(References):

[1]MITRINOVIC D S.Analytic inequalities[M].New York:Springer-Verlag,1970.

[2]HIRZALLAH O.Non-commutative operator Bohr inequality[J].Journal of Mathematical Analysis and Applications,2003,282(2):578-583.

[3]CHEUNGA Wing Sum,PECARICB Josip.Bohr′s inequalities for Hilbert space operators[J].Journal of Mathematical Analysis and Applications,2006,323(1): 403-412.

[4]ZHANG Fuzhen.On the Bohr inequality of operators[J].Journal of Mathematical Analysis and Applications,2007,333(2):1264-1271.

[5]BOHR H.Zur theorie der fastperiodischen funktionen I[J].Acta Mathematic,1926,47(3):237-281.

[6]MITRINOVIC D S,PECARI J E,FINK A M.Classical and new inequalities in analysis[M].Berlin:Springer,1992.

[7]PECARIC J E,DRAGOMIR S S.A refinement of Jensen inequality and applications[J].Studia Universitatis Babes-Bolyai Mathematica,1989,34:15-19.

[8]PECARIC J E,RASSIAS T M.Variations and generalizations of Bohr′s inequality[J].Journal of Mathematical Analysis and Applications,1993,174(1):138-146.

[9]RASSIAS T M.A generalization of a triangle-like inequality due to H. Bohr[J].Abstracts Amer Math Soc,1985(5):276-281.

[10]CHANSANGIAM P.Bohr inequalities in C*-algebras[J].Science Asia,2010,36(4):326-332.

[11]CHANSANGIAM P,HEMCHOTE P,PANTARAGPHONG P.Generalizations of Bohr inequality for Hilbert space operators[J].Journal of Mathematical Analysis and Applications,2009,356(2):525-536.

[12]ZUO H,FUJII M.Matrix order in Bohr inequality for operators[J].Banach Journal of Mathematical Analysis,2010,4 (1):21-27.

[13]MOSLEHIAN M S,RAJNA R.Generalizations of Bohr′s inequality in Hilbert C*-modules[J].Linear & Multilinear Algebra,2010,58(3):323-331.

[14]MOSLEHIAN M S,PECARIC J E,PERIC I.An operator extension of Bohr′s inequality[J].Bulletin of the Iranian Mathematical Society,2008,35(2):67-74.

[15]MATHARU J S,MOSLEHIAN M S.Eigenvalue extensions of Bohr′s inequality[J].Linear Algebra and its Applications,2011,435(2):270-276.

编辑、校对：师琅

DOI：10.13338/j.issn.1006-8341.2016.02.005

Received date：2015-09-11

Foundation item:This work is supported by the S.R.P.F. of Shaanxi Province Education Department (12JK0886) and the S.R.F. of Yulin University(12GK50)

Corresponding author:ZHANG Qiaowei(1983—),female,native of Jiaxian,Shaanxi province,lecturer of Yulin University,research area is operator theory and wavelet analysis.E-mail: zhangqiaowei1188@sohu.com

CLC number:O 177.1

Document code:A

关于C*-代数中Bohr不等式的一个注记

张巧卫1,李文波2

(1.榆林学院 数学与统计学院,陕西 榆林 719000;2.惠州学院 数学系,广东 惠州 516007)

摘要:利用C*-代数到B(H)中的等距*-表示,研究C*-代数中的Bohr不等式,得到了4个推广的Bohr不等式成立的一些充分必要条件.主要结论如下:设p,q∈R+,且满足,则∀A,B∈S(S为有单位元的C*-代数)，|A-B|2+|(1-p)A-B|2≤p|A|2+q|B|2成立当且仅当p≤2;设α,β,u,v∈R, p,q∈R+, 则|αA+βB|2+|uA+vB|2≤p|A|2+q|B|2成立当且仅当p≥α2+u2,q≥β2+v2且(p-(α2+u2))(q-(β2+v2))≥(αβ+uv)2;设a,b∈R+,c∈C,则∀成立当且仅当ab≥|c|2;设α,β∈R,x,y是正数,则∀A,B∈S,|αA+βB|2≤x|A|2+y|B|2成立,当且仅当x≥α2,y≥β2且(x-α2)(y-β2)≥α2β2.

关键词:Bohr不等式;C*-代数;*-表示

ArticleID:1006-8341(2016)02-0161-05

Citationformat：ZHANGQiaowei,LIWenbo.AnoteontheBohrinequalityinC*-algebras[J].纺织高校基础科学学报,2016,29(2)：161-165.

ZHANGQiaowei,LIWenbo.AnoteontheBohrinequalityinC*-algebras[J].BasicSciencesJournalofTextileUniversities,2016,29(2):161-165.