本原不可幂符号矩阵的完全不可分基指数
黄宇飞, 柳柏濂
(1.广州民航职业技术学院, 广州 510403;2.华南师范大学数学科学学院, 广州 510631)
本原不可幂符号矩阵的完全不可分基指数
黄宇飞1*, 柳柏濂2
(1.广州民航职业技术学院, 广州 510403;2.华南师范大学数学科学学院, 广州 510631)
将可分性的概念推广至广义符号方阵中,定义了完全模糊不可分和部分模糊可分的广义符号方阵;把本原(0,1)方阵的(严格)完全不可分指数的概念推广到本原不可幂(广义)符号方阵,提出了(严格)完全不可分基指数的概念并给出了相应的图论刻画,同时获得了若干本原不可幂符号矩阵类的(严格)完全不可分基指数的上界. 进一步地,将完全模糊不可分广义符号矩阵和(严格)完全不可分基指数的概念分别拓展为w-模糊不可分广义符号矩阵和(严格)w-不可分基指数.
本原; 不可幂; (广义)符号矩阵; (严格)完全不可分基指数
1 引言和定义
(0,1)矩阵是元素取自于集合{0,1}的矩阵,其中矩阵元素“0”和“1”的乘法定义为通常的乘法,而加法定义为“1+1=1”(有别于通常的加法). 于是,从代数结构的观点来看,(0,1)矩阵就是熟知的布尔矩阵. 符号矩阵是元素取自于集合{0,1,-1}的矩阵. 对于符号方阵A,注意到:在计算A的幂序列Ak(k=1,2,…)时,由于无法确定“正号”加上“负号”所得的符号,故引入新的记号“#”来表示这样的模糊符号(又称不定号)[1]102. 自然地,集合Γ={0,1,-1,#}中元素的加法和乘法定义如下:

+01-1#·01-1#001-1#00000111##101-1#-1-1#-1#-10-11#######0# ##
我们把元素取自于集合Γ={0,1,-1,#}的矩阵称为广义符号矩阵. 易见,符号矩阵是广义符号矩阵的特例,而(0,1)矩阵又是符号矩阵的特例. (广义)符号方阵A可分为如下2类:如果A的幂序列Ak(k=1,2,…)均不含模糊符号“#”,那么A称为可幂的;否则,A称为不可幂的[1]102. 另外,规定本文所有的矩阵运算均基于集合Γ进行.
众所周知,在矩阵的置换相抵变换下,(0,1)方阵可以划分为完全不可分和部分可分[2]. n阶(0,1)方阵A是完全不可分方阵当且仅当A的任意k×l阶子矩阵皆含有元素“1”,其中1≤k,l≤n且k+l=n. 不是完全不可分的(0,1)方阵称为部分可分方阵. 关于(0,1)方阵的可分性刻画及有关研究成果已较为丰富[2]. 注意到:(0,1)矩阵中的元素“1”,与广义符号矩阵中的元素“#”,在运算中有着相似的作用. 因此,我们考虑将上述可分性的概念推广至广义符号方阵中.
定义1设A是n阶广义符号方阵. 如果A的任意k×l阶子矩阵皆含有元素“#”,其中1≤k,l≤n且k+l=n,则称A为完全模糊不可分的. 不是完全模糊不可分的广义符号方阵称为部分模糊可分广义符号方阵.
记n阶完全模糊不可分广义符号方阵的集合为SFn. 显然,对于ASFn,由于A中必含有元素“#”,故A也是不可幂的广义符号方阵.
n阶(0,1)方阵A是本原的当且仅当存在正整数k使得Ak=Jn,其中Jn是所有元素均为“1”的n阶方阵. 把(广义)符号矩阵A的所有非零元都换成元素“1”,所得的(0,1)矩阵记为|A|. 那么,|A|完全决定了A的零位模式. 进而,称(广义)符号方阵A是本原的,如果|A|是本原的.
考察n阶(广义)符号方阵A的幂序列:A,A2,A3,…,因为(广义)符号方阵对于乘法而言是1个有限半群,即n阶符号方阵至多有3n2个,n阶广义符号方阵至多有4n2个,所以A的幂序列中必然会出现相同的项. 记最先重复出现的1对幂是Ab=Ab+p,其中b和p都是正整数. 我们称p=p(A)为(广义)符号方阵A的(广义)周期,b=b(A)为A的(广义)基指数[1]103.
记所有元素均为“#”的n阶广义符号方阵为#Jn. 文献[3]290已证得:n阶本原不可幂(广义)符号方阵A的基指数b(A)=min{k|Ak=#Jn},周期p(A)=1. 因此,结合定义1可知:对于n阶本原不可幂的(广义)符号方阵A,必存在正整数t(如:t=b(A)),使得AtSFn. 由此给出如下概念.
定义2设A是n阶本原不可幂的(广义)符号方阵. 定义A的完全不可分基指数(记为ρ(A))是最小的正整数t使得AtSFn.
另外,我们发现:对于n阶本原不可幂(广义)符号方阵A,由定义2可知Aρ(A)SFn,但并不保证对所有的正整数i (>ρ(A)),Ai均是完全模糊不可分的. 例如:记n阶本原不可幂符号方阵的集合为SPn.令

定义3设A是n阶本原不可幂(广义)符号方阵. 定义A的严格完全不可分基指数(记为ρ*(A))是最小的正整数t,使得对于满足i≥t的任意正整数i,有AiSFn.
可见,(严格)完全不可分基指数正是本原(0,1)方阵的(严格)完全不可分指数[4-5]在本原不可幂(广义)符号方阵中的拓广. 关于(严格)完全不可分指数的研究已有较丰富的成果[5-8],本文主要针对完全不可分基指数和严格完全不可分基指数展开研究,给出(严格)完全不可分基指数的图论刻画,探索若干本原不可幂符号矩阵类的(严格)完全不可分基指数的上界,并把(严格)完全不可分基指数进一步推广为(严格)w-不可分基指数.
2 (严格)完全不可分基指数的图论刻画


设A是(广义)符号方阵,且记Wk(i,j)为其伴随(广义)带号有向图S(A)中从点i到点j的长为k的有向途径的集合. 则幂Ak中(i,j)位置元素(Ak)ij的符号可确定为:

(1)
由式(1)可知[3]286-287:
(i)(Ak)ij=0当且仅当S(A)中没有从点i到点j的长为k的途径;
(ii)(Ak)ij=1当且仅当Wk(i,j)≠∅且Wk(i,j)中所有途径都同为正号;
(iii)(Ak)ij=-1当且仅当Wk(i,j)≠∅且Wk(i,j)中所有途径都同为负号;
(iv)(Ak)ij=#当且仅当S(A)中有从点i到点j的长为k的SSSD途径对(或有从点i到点j的长为k的符号为“#”的途径).
设SRt(X)表示从点子集X中的任意点出发经过长为t的SSSD途径对(或符号为“#”的途径)所能到达的所有点的集合,又称其为模糊可达集. 对于完全模糊不可分的广义符号方阵A,亦称其伴随广义带号有向图S是完全模糊不可分的. 从图论的角度出发,结合定义1,n阶广义带号有向图S是完全模糊不可分的当且仅当S中任一满足1≤|X|=k≤n-1的k点子集X都有|SR1(X)|≥k+1. 再根据定义2和定义3,可用图论的语言来刻画(严格)完全不可分基指数.
命题1设S是n阶本原不可幂(广义)带号有向图. 那么,S的完全不可分基指数ρ(S)是最小的正整数t,使得S中任一满足1≤|X|=k≤n-1的k点子集X都有|SRt(X)|≥k+1.
命题2设S是n阶本原不可幂(广义)带号有向图. 那么,S的严格完全不可分基指数ρ*(S)是最小的正整数t,使得对于满足i≥t的任意正整数i,S中任一满足1≤|X|=k≤n-1的k点子集X都有|SRi(X)|≥k+1.
另外,记本原不可幂带号有向图S的模糊指标[3]290为r(S),即最小的正整数r使得在S中存在长为r的SSSD途径对;另外,对于本原不可幂的广义带号有向图S,若S中含有带“#”号的弧,则规定r(S)=1. 易见,
r(S)≤ρ(S)≤ρ*(S)≤b(S),
其中b(S)是本原不可幂(广义)带号有向图S的基指数. 故(严格)完全不可分基指数是有意义的(为有限值).
(严格)完全不可分基指数有下述应用背景. 1个n阶本原不可幂(广义)符号方阵对应于1个n阶本原不可幂(广义)带号有向图,即带变极器(及干扰器)的非记忆通讯系统网络(其定义及运作方式参见文献[10]). 设初始状态为任选若干个点(至少1个,至多n-1个)赋予相同的信息,完全不可分基指数描述的是最短的时间t1,使得此时刻比初始状态至少多1个点掌握了该信息的模糊化(即正、负信息相互干扰的结果);而严格完全不可分基指数刻画的则是最短的时间t2,使得从该时刻起的任一时刻都比初始状态至少多1个点掌握了该信息的模糊化.
最后给出关于本原不可幂带号有向图的刻画[3],这是研究本原不可幂符号矩阵的重要工具之一.
引理1[3]288设S是本原带号有向图. 那么,S是不可幂的当且仅当S包含2个有向圈C1和C2(记其长度分别为p1和p2),它们满足以下2个条件之一:
(B1)p1是偶数,p2是奇数, 且sgn(C1)=-1.
(B2)p1和p2都是奇数, 且sgn(C1)=-sgn(C2).
为方便起见,称这样一对满足条件(B1)或(B2)的有向圈C1和C2为“违规圈对”. 由此还可推出: 途径对W1=p2C1和W2=p1C2的长度均为p1p2,但符号相异, 即(sgn(C1))p2=-[(sgn(C2))p1].
3 (严格)完全不可分基指数的界
本节将探索若干本原不可幂符号矩阵(即带号有向图)类的(严格)完全不可分基指数的上界.
首先,考虑恰有d个环的n阶本原不可幂带号有向图集SPn(d)的(严格)完全不可分基指数的上界,其中1≤d≤n. 根据环点的特征及相关记号的意义,可证明下述引理.
引理2设SSPn(d). 若从非空点子集X中的顶点出发通过长为r的SSSD途径对能到达某q个环点,其中1≤q≤d,则对于任意非负整数t,
|SRr+t(X)|≥min{q+t,n}.
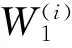
对于任意非负整数t,由于v1,…,vq都是环点,故存在min{q+t,n}个顶点(记为uj(j=1,…,min{q+t,n})),分别能从{v1,…,vq}中某些环点出发通过长为t的途径到达,不妨设点uj可从环点vhj出发通过长为t的途径Pj到达,其中j=1,…,min{q+t,n},而hj{1,…,q}.
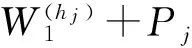
引理3设SSPn(d),且每个环均与有向圈C1构成违规圈对. 则
ρ(S)≤ρ*(S)≤2n-d+1.
证明根据定义2和定义3,显然有ρ(S)≤ρ*(S). 任取1个满足1≤|X|=k≤n-1的点子集X. 结合命题1和命题2,仅需证明对于满足η≥2n-d+1的任意正整数η,都有|SRη(X)|≥k+1.
不妨设有向圈C1的长度为p1,S中的d个环点记为v1,…,vd,其上的环又分别记为L1,…,Ld. 不失一般性,又设v1,…,vt不在有向圈C1上,而vt+1,…,vd在有向圈C1上,其中0≤t≤d.
情形1:t=d,即所有的环点均不在有向圈C1上. 故p1≤n-d. 记从有向圈C1中的点(不妨记其为u0)到某个环点(不妨记其为vh, 1≤h≤d)的最短有向路为Q,故Q的长度t1≤n+1-d-p1. 注意到:每个环均与有向圈C1构成违规圈对,从而C1+Q与Q+p1Lh是长为p1+t1的SSSD途径对. 又记从X中的点(不妨记为x0)到点u0的最短途径为P,易见其长度t2≤n+1-k-1=n-k. 对于满足η≥2n-d+1的任意正整数η,由于
p1+t1+t2≤p1+(n+1-d-p1)+(n-k)=
2n-d+1-k≤η-k,
不妨设μ=(η-k)-(p1+t1+t2),显然μ≥0. 因此,P+(C1+Q)+μLh与P+(Q+p1Lh)+μLh是从点x0X到环点vh的长为η-k的SSSD途径对. 从而由引理2可得:|SRη(X)|=|SR(η-k)+k(X)|≥1+k.
情形2: 0≤t≤d-1,即有d-t(≥1)个环点在有向圈C1上. 故p1Lj与C1是从点vj到自身长为p1的SSSD途径对,其中j=t+1,…,d. 易见,p1≤n-t.

p1≤n-t≤(η-n+d-1)-t,

|SRη(X)|=|SR(η-n+d-1-t)+(n+t-d+1)(X)|≥
(k+d-t-n)+(n+t-d+1)=k+1.
子情形2.2:n+1-k-d+t>0. 此时,存在从X中的点(不妨记其为x0)到有向圈C1上的某个环点(不妨记其为vh,t p+p1≤[n+1-k-(d-t)]+(n-t)=2n-d+1-k≤η-k, 不妨设μ=(η-k)-(p+p1),则μ≥0. 从而,P+p1Lh+μLh与P+C1+μLh是从点x0X到环点vh的长为η-k的SSSD途径对. 结合引理2,有:|SRη(X)|=|SR(η-k)+k(X)|≥1+k. 证毕. 引理4设SSPn(d),且所有环的符号不全相同. 则 ρ(S)≤ρ*(S)≤2n-d+1. 证明任取1个满足1≤|X|=k≤n-1的点子集X. 不妨记SSPn(d)的d个环点为v1,…,vd,其上的环又分别记为L1,…,Ld. 由于S中所有环的符号不全相同, 故d≥2. 根据命题1和命题2,下面证明:对于满足η≥2n-d+1的任意正整数η,有|SRη(X)|≥k+1. 情形1:n+1-k-d>0. 记从X中的点(不妨记其为x)到某个环点(不妨记为vh1, 1≤h1≤d)的最短有向路为P,故P的长度t1≤n+1-k-d. 注意到:必存在环点vh2(1≤h2≤d)满足sgn(Lh1)=-sgn(Lh2),从而Lh1和Lh2构成违规圈对. 又记从点vh1到点vh2的最短路为Q,则其长度t2≤n-1. 对于满足η≥2n-d+1的任意正整数η,由于t1+t2+1≤(n+1-k-d)+(n-1)+1≤η-k,记μ=(η-k)-(t1+t2+1),则μ≥0. 从而P+Lh1+Q+μLh2和P+Q+Lh2+μLh2是从点xX到环点vh2的长为η-k的SSSD途径对. 故由引理2可得:|SRη(X)|=|SR(η-k)+k(X)|≥1+k. 对于满足η≥2n-d+1的任意正整数η,注意到: t1+1≤2n-d+1-k≤η-k, |SRη(X)|=|SR(η-k+1)+(k-1)(X)|≥2+(k-1)=k+1. 证毕. 情形1: 1≤m≤n-d.故从点vm到某环点(显然是环点vn-d+1)的最短有向路的长度为n-d+1-m. 由于-(n-d+1-m)-n≤m-1≤n-d-1≤n-2,故不存在从点vm到点vn-d的长为的SSSD途径对,其中m=1,…,n-d. 情形2:n-d+1≤m≤n-1.因为从点vm到点vn-d的最短有向路之长为2n-m-d,且2n-m-d≥n-d+1,又-n≤n-d,所以也不存在从点vm到点vn-d的长为的SSSD途径对,其中m=n-d+1,…,n-1. 定理1设SSPn(d),则 ρ(S)≤ρ*(S)≤2n-d+1, 证明由于SSPn(d),故根据引理1,S包含违规圈对C1和C2(记其长度分别为p1和p2),它们满足以下2个条件之一: (B1)p1是偶数,p2是奇数, 且sgn(C1)=-1. (B2)p1和p2都是奇数, 且sgn(C1)=-sgn(C2). 情形1:C1和C2符合条件(B1). 因为环的长度是1(即奇数),所以每个环均与C1构成违规圈对,从而由引理3可得: ρ(S)≤ρ*(S)≤2n-d+1. 情形2:C1和C2符合条件(B2). 若S中所有环的符号均相同,由于环的长度是1(即奇数),故每个环均与C1(或C2)构成违规圈对. 同样,由引理3可得: ρ(S)≤ρ*(S)≤2n-d+1.若S中所有环的符号不全相同,则由引理4亦得: ρ(S)≤ρ*(S)≤2n-d+1. 记迹非零的n阶本原不可幂符号矩阵之集为SPNn. 由于SSPNn至少含有1个环点,故根据定理1可得如下的推论. 推论1设SSPNn,则ρ(S)≤ρ*(S)≤2n,此上界可达且是极图之一. 定理2设SSPn有长为s的有向圈,且有t(≥s)个顶点落于某长为s的有向圈上,则 ρ(S)≤s(2n-t+1). 证明设SSPn的邻接符号矩阵为A. 由于S是本原不可幂的,故S(As)(又记为Ss)也是本原不可幂的. 又因为S有长为s的有向圈,且有t (≥s)个顶点落于某长为s的有向圈上,所以Ss含有t个环点,即SsSPn(t). 根据定理1可得: ρ*(Ss)≤2n-t+1, 结合定义2和定义3可得: ρ(S)≤s·ρ*(Ss)≤s(2n-t+1). 证毕. 由定理2可得以下推论,从而导出若干特殊本原不可幂带号有向图类的完全不可分基指数的上界. 推论2设SSPn且有1个哈密顿圈,则ρ(S)≤n(n+1). 证明若SSPn且有1个哈密顿圈,则S的所有点(即n个点)均落于长为n的有向圈上. 由定理2可得:ρ(S)≤n(2n-n+1)=n(n+1). 证毕. 推论3设SSPn且其直径为d,则ρ(S)≤2d(2n-d). 证明由于S的直径为d,则其存在长为s≤2d的有向圈,包含t≥d+1个不同的顶点. 由定理2导出:ρ(S)≤2d[2n-(d+1)+1]=2d(2n-d). 证毕. 推论4设SSSn(n阶本原不可幂对称符号矩阵集),则ρ(S)≤2(n+1). 证明因为SSSn,所以S的所有点(即n个点)均分别落于某个长为2的有向圈上. 结合定理2,有:ρ(S)≤2(2n-n+1)=2(n+1). 证毕. 推论5设SSTn(n阶本原不可幂竞赛符号矩阵集),则ρ(S)≤3(n+1). 证明若SSTn,则S的所有点(即n个点)均分别落于某个长为3的有向圈上. 根据定理2可得:ρ(S)≤3(2n-n+1)=3(n+1). 证毕. 作为完全不可分矩阵的推广,SHEN等[11]引进了w-不可分矩阵,并把(严格)完全不可分指数的研究推广至(严格)w-不可分指数的研究上,其中w是满足-n 定义4设A是n阶广义符号方阵,且w是满足-n 注1设A是n阶广义符号方阵. 易见,A是(1-n)-模糊不可分的当且仅当A不是实矩阵,而A是(n-1)-模糊不可分的当且仅当A=#Jn. 特别地,1-模糊不可分广义符号方阵正是完全模糊不可分广义符号方阵. 对于w-模糊不可分的广义符号方阵A,亦称其伴随广义带号有向图S是w-模糊不可分的. 用图论的语言,n阶广义带号有向图S是w-模糊不可分的当且仅当S中任一满足1≤|X|=k≤min{n,n-w}的k点子集X都有|SR1(X)|≥k+w. 根据定义4,不难发现:(1)w1-模糊不可分广义符号方阵必然是(w1-1)-模糊不可分的,其中w1是满足-n+1 定义5设A是n阶本原不可幂(广义)符号方阵,且w是满足-n 用图论的语言来描述w-不可分基指数,有下述命题. 命题3设S是n阶本原不可幂(广义)带号有向图,且w是满足-n 注意到:对于n阶本原不可幂(广义)符号方阵A,虽然Aεw(A)是w-模糊不可分的广义符号方阵,但是并不保证对所有的正整数i (>εw(A)),Ai均是w-模糊不可分的. 因此,我们提出以下严格w-不可分基指数的概念. [1]LIZS,HALLF,ESCHENBACHCA.Ontheperiodandbaseofasignpatternmatrix[J].LinearAlgebraandItsApplications, 1994, 212/213(94). [2]柳柏濂. 组合矩阵论[M]. 北京: 科学出版社, 2005: 60-65. [3]YOULH,SHAOJY,SHANHY.Boundsonthebasesofirreduciblegeneralizedsignpatternmatrices[J].LinearAlgebraandItsApplications, 2007, 427(2/3). [4]SCHWARZ.ThesemigroupoffullyindecomposablerelationsandHallrelations[J].CzechoslovakMathematicalJournal, 1973, 23:151-163. [5]BRUALDIRA,LIUBL.Fullyindecomposableexponentsofprimitivematrices[J].ProceedingsoftheAmericanMathematicalSociety, 1991, 112(4):1193-1201. [6]CHAOCY.Onaconjectureofthesemigroupoffullyindecomposablerelations[J].CzechoslovakMathematicalJournal, 1977, 27:591-597. [7]CHAOCY,ZHANGMC.Onthesemigroupoffullyindecomposablerelations[J].CzechoslovakMathematicalJournal, 1983, 33:314-319. [8]LIUBL.OnfullyindecomposableexponentsforprimitiveBooleanmatriceswithsymmetricones[J].LinearandMultilinearAlgebra, 1992, 31:131-138. [9]BONDYJA,MURTYUSR.Graphtheorywithapplications[M].London:TheMacmillanPressLtd, 1976. [10]柳柏濂, 黄宇飞. 组合矩阵的结构指数[M]. 北京: 科学出版社, 2015:30-33. [11]SHENJ,GREGORYD,NEUFELDS.Exponentsofindecomposability[J].LinearAlgebraandItsApplications, 1999, 288(1):229-241. 【中文责编:庄晓琼英文责编:肖菁】 Fully Indecomposable Bases of Primitive Non-Powerful Sign Pattern Matrices HUANG Yufei1*, LIU Bolian2 (1.Guangzhou Civil Aviation College, Guangzhou 510403, China;2.School of Mathematical Sciences, South China Normal University, Guangzhou 510631, China) The definition of indecomposability for generalized sign pattern matrices is extended firstly in this paper. The fully ambiguous indecomposable generalized sign pattern matrices and partly ambiguous decomposable generalized sign pattern matrices are then defined. Moreover, the (strict) fully indecomposable base for a primitive non-powerful (generalized) sign pattern matrix is put forward, which is the generalization of the (strict) fully indecomposable exponent for a primitive (0,1) matrix. Meanwhile, the graph depicts for (strict) indecomposable base is given, and some upper bounds for the (strict) fully indecomposable base of primitive non-powerful sign pattern matrices are obtained. Furthermore, the definitions of fully ambiguous indecomposable generalized sign pattern matrix and (strict) fully indecomposable base tow-ambiguous indecomposable generalized sign pattern matrix and (strict)w-indecomposable based are generalized respectively. primitive; non-powerful; (generalized) sign pattern matrix; (strict) fully indecomposable base 2015-12-18《华南师范大学学报(自然科学版)》网址:http://journal.scnu.edu.cn/n 国家自然科学基金青年科学基金项目(11501139) 黄宇飞,讲师,Email: fayger@qq.com. O151.21 A 1000-5463(2016)04-0088-07
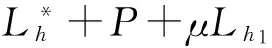


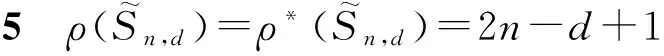

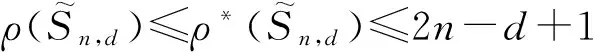


4 完全不可分基指数的推广




