冯·诺依曼子代数的分离投影

严 倩，刘 倩，吴文明

（1.重庆师范大学　数学科学学院，重庆401331；2.河南省南阳市第五中学，河南　南阳 473000）

冯·诺依曼子代数的分离投影

严 倩1，刘 倩2，吴文明1

（1.重庆师范大学数学科学学院，重庆401331；2.河南省南阳市第五中学，河南南阳 473000）

引入了冯·诺依曼代数的子代数的分离投影的概念，然后刻画了矩阵代数中其子代数分离投影的存在性，构造了可分无限Hilbert特空间上子代数的分离投影。具体地，设M=Mn（C）⊗Mn（C），N=Mn（C）⊗C1n，证明了N在M中存在维数为r（1≤r≤n2-1）的分离投影。

冯·诺依曼代数；子代数；分离投影；张量积

0 引 言

算子理论和算子代数是泛函分析中的重要研究课题。其中，自反格、可迁格是综合算子代数和算子理论的研究对象。具体来说，设 H为复Hilbert空间，B（H）是 H上全体有界线性算子的集合，P（B（H））为 B（H）中全体投影构成的集合。设S⊂B（H）为非空子集，S中所有算子公共不变子空间的集合称为S的不变子空间（即不变投影）格，即：Lat（S）=｛p∈P（B（H））：（1H-p）tp=0，∀t∈S｝构成的格，1H为H上的恒等算子。对于P（B（H））的非空子集L，A1g（L）=｛a∈B（H）：（1H-p）ap=0，∀p∈L｝表示保持L中的每个投影都不变的有界线性算子全体构成的代数。A1g（L）是B（H）中在弱算子拓扑下的闭子代数。一般地，总有L⊆Lat（A1g（L））和S⊆A1g（Lat（S））。如果等号成立，则分别称L为自反格，S为自反子代数。如果A1g（L）≌ ，则称L是可迁的。

Halmos于1970年在文章［1］中提出了十个关于算子理论的问题，其中一个是最小数目可迁格的存在性问题。容易验证，只有一个或两个非平凡投影的格不是可迁的，存在只有3个非平凡投影的可迁格。然而，在一类特殊的Ⅱ1型因子（因子是一类特殊的冯·诺依曼代数，其一般理论可见［2］）中，J.P.Bannon［3］证明了存在具有12个非平凡投影的可迁格，并且当Ⅱ1型因子由两个自伴元生成时，则该Ⅱ1型因子中存在由5个非平凡投影构成的可迁格。葛力明和袁巍在文献［4］证明了Ⅱ1型因子中只含3个非平凡投影的双三角格一定不是可迁的。因此，一个自然的问题是：在Ⅱ1型因子中，是否存在由4个非平凡投影构成的可迁格？

最近，D.Hadwin［5］等在超有限的Ⅱ1型因子R中构造了一个附属于R的无界算子，使得该无界算子在R中的相对换位子是平凡的。从而可以在R中构造只有4个非平凡投影的可迁格。具体来说，设t是附属于Ⅱ1型因子R的无界算子，使得对于任意a∈R，如果t-1at=a成立，则有a为恒等算子的系数倍。

现设 t的极分解为t=kw，在M=R⊗M2（C）中，记，其中h=k2（1+k2）-1且v=-w。令L=｛0，1，p1，p2，p3，p4｝，则L是由M中4个非平凡投影构成的可迁格。

众所周知，Ⅱ1型因子上存在一个忠实的正规的迹态，记为τ。从而上述格L的可迁性等价于在M中存在一个迹为1/2的投影q，使得任意的算子，如果，其中1H⊗C2为M中的单位元（即恒等算子），则有a∈C1H。

有限维的有限因子就是矩阵代数，因此一个自然的问题是：上述结论在矩阵代数中是否成立？而矩阵代数中一个投影在迹态下的取值即为该投影值域空间的维数除以矩阵的阶数。从而，研究问题就归结为：

设M=Mn（C）⊗M2（C），N=Mn（C）⊗C12，从而N⊆M。是否存在维数为n的投影p∈M使得：当t∈N且满足（12n-p）tp=0时，一定有t为单位矩阵的系数倍？为此引入如下定义。

定义1 设H是一个复的Hilbert空间，M⊆B（H）是一个子代数，N是M的子代数。称投影p∈M是N在M中的分离投影，如果对任意t∈N，只要（1H-p）tp=0成立，则t一定为恒等算子的系数倍。

主要研究矩阵代数的子代数的分离投影的存在性。文章第一部分将证明在一定条件下，矩阵代数的子代数的分离投影是存在的。然后在第二部分中将给出可数无限维Hilbert空间上一个分离投影存在的例子。

1 矩阵代数中子代数的分离投影

1.1 主要问题及符号说明

根据序言，本节将讨论以下问题：

设 M=Mn（C）⊗Mn（C），N=Mn（C）⊗C1n，M中是否存在维数为1≤r≤n2-1的投影为N的分离投影？即：是否存在维数为1≤r≤n2-1的投影p∈M使得：当t∈N且满足（1n2-p）tp=0时，一定有t为单位矩阵的倍数？

为了方便，本文总假设t=a⊗1n，a∈Mn（C），1n为n阶单位矩阵。设｛e1，e2，…，en｝为有限维复Hilbert空间Cn中的标准正交基，其中ei表示第i个分量为1，其它分量为0的单位向量。

1.2 主要结果和证明

引理1 设 M=Mn（C）⊗Mk（C），N=Mn（C）⊗C1k，则在M中存在N的r-维分离投影当且仅当存在N的（nk-r）-维分离投影。

证明 假设p是N维数为r的分离投影，则对任意t∈N且满足（1nk-p）tp=0时，一定有t为单位矩阵的倍数。

由于

（1nk-p）tp=0⇔p*t*（1nk-p*）=0⇔（1nk-q）t*q=0，其中q=1nk-p为p的正交补投影且q的维数为nk-r。

因此，（1nk-p）tp=0推出t为单位矩阵的倍数等价于（1nk-q）t*q=0推出t*为单位矩阵的倍数。证毕。

命题1 设M=Mn（C）⊗Mn（C），N=Mn（C）⊗C1n，则存在N在M中的维数为1的分离投影。

证明 设ξ=（e1，e2，…，en）T∈Cn2。令p是从Cn2到由向量ξ张成的闭线性子空间的正交投影。当t= a⊗1n∈N使得（1n2-p）tp=0成立时，则存在常数λ∈C使得：tξ=λξ。

从而有：ae1=λe1，ae2=λe2，…，aen=λen。故有：a=λ1n。证毕。

N在M中存在维数为2的分离投影的存在性与n的取值有关。根据n值的不同，有不同的结论。

命题2 当n=2时，对任意维数为2的投影p∈M，都存在t∈NC14使得（14-p）tp=0。

证明 对于任意两个向量ξ1=（ξ1，1，ξ1，2）T，ξ2=（ξ2，1，ξ2，2）T∈C4，其中 ξi，j∈C2，i，j=1，2。令［ξ1，ξ2］表示由ξ1，ξ2张成的线性子空间。p是从C4到子空间［ξ1，ξ2］的正交投影。

情形1：两个向量组ξ1，1和ξ2，1、ξ1，2和ξ2，2中至少有一组线性无关，不妨设ξ1，1和ξ2，1线性无关。

此时，由于ξ1，1和ξ2，1张成空间C2，因此存在可逆矩阵b∈M2（C）使得：bξ1，1=e1，bξ2，1=e2。

记η1，2=bξ1，2，η2，2。则存在矩阵c使得ce1=η1，2，ce2=η2，2。

令ηi=（ei，ηi，2）T，i=1，2。注意：

若c不是单位阵的倍数，那么令x=c，则易见：

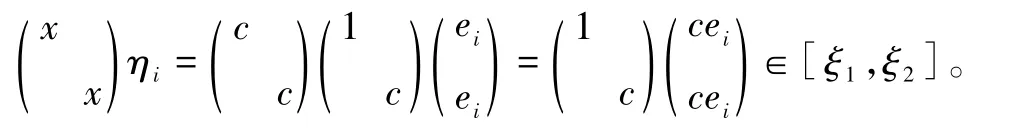
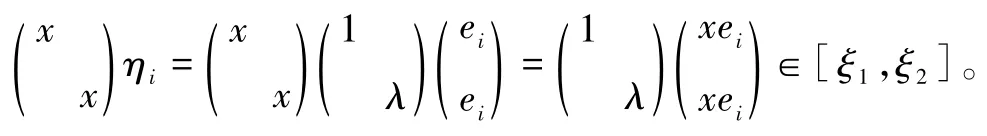
情形 2：两个向量组ξ1，1和ξ2，1、ξ1，2和ξ2，2都是线性相关的。由于［ξ1，ξ2］是2维线性子空间，故存在可逆的线性变换使得ξ1，ξ2分别变为：ξ′1=（ξ′1，1，0）T，ξ′2=（0，ξ′2，2）T。因此不妨设：

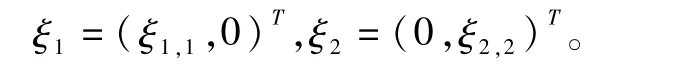
若［ξ1，1，ξ2，2］=C2，则存在可逆矩阵b1∈M2（C）使得：b1ξ1，1=e1，b1ξ2，2=e2。

记η1=（e1，0）T，η2（0，e2）T。此时取，λ1≠λ2。则不是单位阵的倍数且使得（14-p）tp=0。

若ξ2，2∈［ξ1，1］，存在可逆矩阵b2∈M2（C）使得b2ξ1，1=e1，b2ξ2，2=λe1，其中λ为非零复数。此时取x，其中μ≠0。则不是单位阵的倍数且满足（14-p）tp=0。证毕。

推论1 当n=2时，任意维数为2的投影p∈M都不是N的分离投影。

命题3 设M=Mn（C）⊗Mn（C），N=Mn（C）⊗C1n。当 n≥3时，在 M中存在N的维数为2的分离投影。

证明 取两个向量ξ1=（e1，e2，…，en-1，0）T，ξ2=（0，…，0，e1，en）∈Cn2。令p是从 Cn2到［ξ1，ξ2］张成的线性子空间的正交投影。当t=a⊗1n∈N满足（1n2-p）tp=0时，则有：

tξi=λi，1ξ1+λi，2ξ2，i=1，2。

当i=1时，由ae1=λ1，1e1，ae2=λ1，1e2，…，aen-2=λ1，1en-2，aen-1=λ1，1en-1+λ1，2e1和a0=λ1，10+λ1，2en得到 λ1，2=0，aen-1=λ1，1en-1。

当i=2时，由a0=λ2，1e1得到λ2，1=0。从而有：ae1=λ2，2e1，aen=λ2，2en。因此，得到λ1，1=λ2，2。故a等于单位阵的λ1，1倍，因此t为单位阵的倍数。故p是N的分离投影。证毕。

定理1 设M=Mn（C）⊗Mn（C），N=Mn（C）⊗C1n。当n≥3时，在M中存在N的维数为r的分离投影，其中1≤r≤n2/2。

证明 维数等于1、2的情况已证毕。现再从以下情形进行讨论：，1＜i＜r，和ξr=（en，02，…，0，e1）T。令p是从Cn2到线性子空间［ξ1，ξ2，…，ξr］的正交投影。当t=a⊗1n∈N满足（1n2-p）tp =0时，有方程组：

其中λi，j，i，j=1，2，…，r为复数。

由（1）式中i=1时可得：

所以λ1，2=λ1，3=…=λ1，r=0。从而有：aei=λ1，2ei，i=1，2，…，n-r+2。

由（1）式中i=2，…，r-1可得：

所以λ1，1=λi，i，2≤i≤r-1。从而有：aei=λ1，1ei，i=1，2，…，n。

综上可知，a是单位阵的倍数，从而t为单位阵的倍数。故p是N在M中维数为r（3≤r≤n）的分离投影。

其中λi，j，i，j=1，2，…，n+1为复数。

由（2）式中i=1可得：λ1，2=…=λ1，n+1=0，ae1=λ1，1e1。

由（2）式中 i=2，…，n可得：aei=λi，iei，i=2，…，n。

再由（2）中 i=n+1可得：λn+1，1=…=λn+1，n=0，a（e1+…+en）=λn+1，n+1（e1+…+en）。

然而，根据先前的结果有：a（e1+…+en）=λ1，1e1+…+λn，nen。因 此 有：λ1，1=…=λn，n=λn+1，n+1。故t为单位阵的倍数。从而p是N在M中维数为r=n+1的分离投影。

其中λij，i，j=1，2，…，r为复数。

由（3）式中i=1可得：ae1=λ1，1e1。

由（3）式中 i=2可得：ae2=λ2，1e1+λ2，2e2，ae2=λ2，2e2+λ2，n+2e3+λ2，n+3e4+…。

从而有：λ2，1=λ2，n+3=λ2，n+4=…=0，且ae2=λ2，2e2。

类似地由（3）式中i=3，4，…，n可得：aei=λiiei，i=3，…，n。

再由（3）中i=n+1可得：a（e1+…+en）=λn+1，n+1（e1+…+en）。从而t为单位阵的倍数。因此p是N在M中维数为r的分离投影。证毕。

2 可分无限Hilbert空间的一个结果

设H是可分的无限维Hilbert空间，B（H）是作用在H上所有有界线性算子形成的von Neumann代数。令en∶n=1，2，…是H的一组标准正交基。

定理2 设M=B（H）⊗B（H），N=B（H）⊗C1H。存在正交投影p，使得任意的a⊗1H∈N，若（1H⊗H-p）（a⊗1H）p=0成立，则a一定等于恒等算子的倍数，故p是N在M中的分离投影。

证明 取ξn=en⊗en+2en+1⊗en+1，n=1，2，…。令p是从H⊗H到由向量ξ1，ξ2，…张成的闭线性子空间上的正交投影。若a⊗1H∈N满足（1H⊗H-p）（a⊗1H）p=0，则有：

［1］HALMOS P R.Ten problems in Hilbert space［J］.Bulletin of the American Mathematical Society，1970，76（5）：887-933.

［2］KADISON R，RINGROSE J.Fundamentals of the operator algebras［M］.Orlando：Academic Press，1983 and 1986.

［3］BANNON J P.Transitive families of projections in factors of typeⅡ1［J］.Proc.Amer.Math.Soc.，2004，133（1）：834-840.

［4］GE L，YUAN W.Kadison-Singer algebras，Ⅱ1-finite case［J］.Proc Natl.Acad.Sci.USA，2010，107（11）：4840-4844.

［5］HADW IN D，SHEN JH，WU W M，et al.Relative commutnats of an unbounded operator affiliated with a finite von Neumann algebra［J］.Journal of operator theory，2016，1（75）：209-223.

The Separating Projection of von Neumann Subalgebras

YAN Qian1，LIU Qian2，WUWenming1
（1.School of Mathematical Science，Chongqing Normal University，Chongqing 401331，China；2.The Fifth Middle School，Nanyang Henan 473000，China）

This article first introduces the concept of the separating projection of a von Neumann subalgebra in a von Neumann algebra，and exp lores the existence of the separating projection of a subalgebra in a matrix algebra.Then an example of the existence of the separating projection for a separable infinite dimensional Hilbert space is constructed.

von Neumann algebra；subalgebra；separating projection；tensor product

O177.1

A

10.16246/j.issn.1673-5072.2016.01.008

1673-5072（2016）01-0056-05

2016-01-21

国家自然科学基金项目（11271390）

严 倩（1989—），女，云南宣威人，硕士研究生，主要从事算子代数和算子理论研究。

吴文明（1972—），男，四川南充人，博士，教授，硕士生导师，主要从事算子代数和算子理论研究。E-mail：cqnu@cqnu.edu.cn