浅谈圆锥曲线最值处理策略

筅江苏省徐州市第三中学　牛含冰

浅谈圆锥曲线最值处理策略

筅江苏省徐州市第三中学牛含冰

圆锥曲线的最值问题是高考常考题型，解答此类问题的途径是利用平面几何的几何性质及坐标法、代入消元法、根与系数的关系等，将几何问题代数化后，构造目标函数，再利用相关方法求函数的最值，下面通过引例加以说明.

引例设P，Q分别为圆x2＋（y-6）2＝2和椭圆＋y2＝1上的点，则P，Q两点间的最大距离是（%）.

解析：设圆心为点C，则圆x2＋（y-6）2＝2的圆心为C（0，6），半径r＝.设点Q（x0，y0）是椭圆上任意一点，则

点评：本题解答中利用坐标法将几何问题代数化后，构造出目标函数为二次型，进而利用二次函数配方法求最值.求解中注意椭圆中x，y的取舍范围，即-a≤x≤a，-b≤y≤b.

除了二次函数配方法求最值外，还常涉及以下几种方法.

一、利用三角函数的有界性

例1同引例.

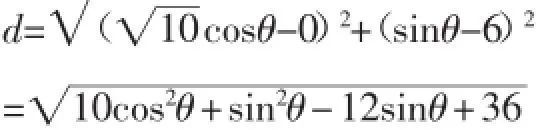
点评：圆锥曲线的参数方程建立了其与三角之间的联系.同理圆心在（x0，y0）半径为r的圆的参数方程为参数θ为圆心角）；双曲线=1的参数

同样可求得D到直线AC的距离：d2≤

所以SABCD≤

点评：A、C两点在椭圆上，A（5，0），C（0，4），欲求四边形ABCD面积的最大值，可将四边形分成两个三角形，显然A、C是定点，则|AC|为定值，因此四边形应分成△ADC，△ABC，只要分别在AC两侧椭圆弧上求一点，使它到AC的距离最远即可.本题最值求解中利用了函数f（x）=Asin（ωx+φ）的性质.

二、利用均值不等式法

（Ⅰ）证明：OT平分线段PQ（其中O为坐标原点）；

解析：（Ⅰ）证明：由题意可知，F的坐标是（-2，0），设T点的坐标为（-3，m），则直线TF的斜率

当m≠0时，直线PQ的斜率kPQ＝，直线PQ的方程是x＝my-2.

当m＝0时，直线PQ的方程是x＝-2，也符合x＝my-2的形式.

设P（x1，y1），Q（x2，y2），将直线PQ的方程与椭圆C的

点评：此类最值问题是高考重点.通过坐标法、代入消元法、判别式及根与系数的关系，所几何问题代数化后构造出目标函数，再将目标函数转化为适合均值不等式的类型.解题中若没找到构造均值不等式的途径，可先用换元法简化函数式结构，如本题中在求出目标函数后，可假设m2+1=t，则目标函数可转化为从而将均值不等式的形式显现出来.

三、利用导数法

例3在平面直角坐标系xOy中，F是抛物线C：x2= 2py（p＞0）的焦点，M是抛物线C上位于第一象限内的任意一点，过M，F，O三点的圆的圆心为Q，点Q到抛物线C的准线的距离为

（Ⅰ）求抛物线C的方程.

（Ⅱ）是否存在点M，使得直线MQ与抛物线C相切于点M？若存在，求出点M的坐标；若不存在，说明理由.

解：（Ⅰ）x2=2y.

设A（x1，y1），B（x2，y2），则有

点评：本题求解中利用点到直线的距离、圆的几何性质结合坐标法、消元法、根与系数的关系以及弦长公式等，求得的目标函数为高次函数，可考虑用导数法求最值.上述解答中先通过换元，将目标函数降次，再利用导数求最值.Z